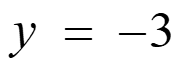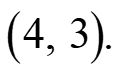Geometry in the Coordinate Plane
Bellwork
1.
There are two different points on the line that are
exactly 10 units from the point
Find the coordinates of the
points.
Perimeter and Area in the
Coordinate Plane
Section 1.4
Classify the polygon by the number of sides.
Tell whether it is convex or concave.
Finding Perimeter in the Coordinate Plane
1.
Find the perimeter of
△
ABC with vertices A(−2, 3), B(3, −3), and
C(−2, −3).
Find the perimeter of the polygon with the
given vertices.
1.
G(2, 4), H(2, −3), J(−2, −3), K(−2, 4)
2.
Q(−3, 2), R(1, 2), S(1, −2), T(−3, −2)
3.
U(−2, 4), V(3, 4), W(3, −4)
4.
Finding Area in the Coordinate Plane
Find the area of
△
DEF with vertices D(1, 3), E(4, −3), and F(−4, −3).
1.
Draw the triangle in a coordinate plane by plotting the vertices and
connecting them.
2.
Find the lengths of the base and height.
3.
Substitute the values for the base and height
into the formula for the area of a triangle.
Find the area of the polygon with the given
vertices.
1.
W(0, 0), X(0, 3), Y(−3, 3), Z(−3, 0)
2.
N(−2, 1), P(3, 1), Q(3, −1), R(−2, −1)
3.
The content discusses various topics related to geometry in the coordinate plane, including finding points on a line that are a specific distance apart, classifying polygons by their sides, determining perimeters of polygons with given vertices, and calculating areas of triangles and polygons. It provides visual representations and step-by-step instructions for solving problems in the coordinate plane.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Bellwork y = There are two different points on the line that are exactly 10 units from the point Find the coordinates of the points. 3 1. ( ) 4, 3 .
Perimeter and Area in the Coordinate Plane Section 1.4
Classify the polygon by the number of sides. Tell whether it is convex or concave.
Finding Perimeter in the Coordinate Plane 1. Find the perimeter of ABC with vertices A( 2, 3), B(3, 3), and C( 2, 3).
Find the perimeter of the polygon with the given vertices. 1. G(2, 4), H(2, 3), J( 2, 3), K( 2, 4) 2. Q( 3, 2), R(1, 2), S(1, 2), T( 3, 2) 3. U( 2, 4), V(3, 4), W(3, 4) 4.
Finding Area in the Coordinate Plane Find the area of DEF with vertices D(1, 3), E(4, 3), and F( 4, 3). 1. Draw the triangle in a coordinate plane by plotting the vertices and connecting them. 2. Find the lengths of the base and height. 3. Substitute the values for the base and height into the formula for the area of a triangle.
Find the area of the polygon with the given vertices. 1. W(0, 0), X(0, 3), Y( 3, 3), Z( 3, 0) 2. N( 2, 1), P(3, 1), Q(3, 1), R( 2, 1) 3.
