Determining Plane Traces and Projections in Geometry

This content covers various exercises related to determining horizontal and vertical traces, as well as projections of lines and points in a given plane. It includes scenarios with parallel and intersecting lines, as well as the determination of planes using points and non-collinear points. The exercises provide a comprehensive understanding of plane geometry concepts.

• Geometry
• Plane Traces
• Projections
• Lines
• Points

adolfina Follow

Uploaded on Aug 21, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

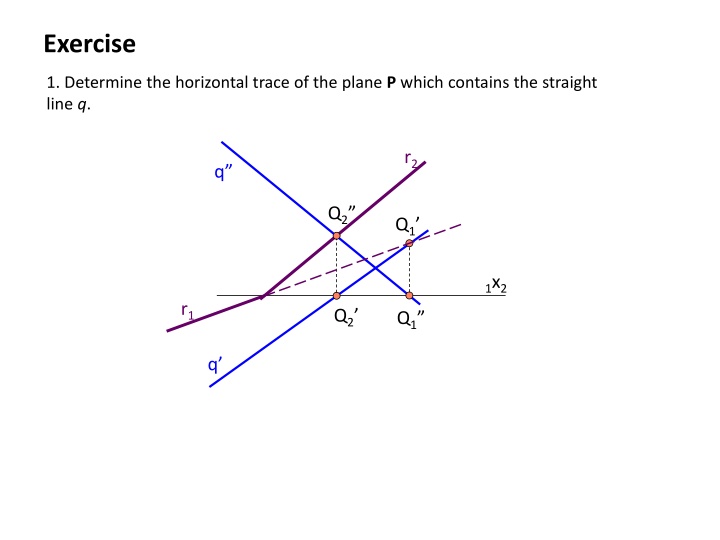
1. Exercise 1. Determine the horizontal trace of the plane P which contains the straight line q. r2 q Q2 Q1 1x2 r1 Q2 Q1 q

2. 2. Determine the vertical projection of the line a contained in the plane . b) a) a a s2 s2 A2 A1 A2 A1 x A1 x A2 A1 s1 s1 a a A2

3. c) d) s2 = a s2 x x a s1 a s1 Remark: if the plane is a horizontal projection plane, then the vertical projection of the line a can not be determined.

4. 3. Determine the vertical projection of the principal line. b) Determine the vertical projection of the vertical principle line m of the plane P. a) Determine the vertical projection of the horizontal principle line a of the plane . m r2 s2 a M1 A2 m A2 x x M1 s1 r1 a

5. 4. Determine the vertical projection of the 1st steepest line a in the plane . 5. Detremine the traces of the plane for which the line p is the 2nd steepest line of the plane. s2 s2 a . P2 p A2 A1 x P1 P2 x A1 p s1 . s1 a P1 A2

6. 6. Determine the projection of a point. a) By using the 1st steepest line determine the vertical projection of the point T in the plane . b) By using the vertical principle line determine the horizontal projection of the point T in the plane . s2 T b s2 m B1 x T B1 B2 M1 m . s1 T x T M1 s1 b B2 Remark: a point in a plane is determined by any line lying in the plane that passes throught the point

7. 7. Determine the horizontal projection of a line segment AB in the given plane . P1 s2 A B P2 s A p 1x2 P2 P1 s s1 B p

8. Contruction of the traces of a plane determined by b) two parallel lines a) two intersecting lines A2 r2 B2 n a b m M1 S M2 r2 N2 N1 A1 x B1 x M1 M2 A2 B2 N2 S N1 A1 a n b m r1 r1 B1 A plane can determined also with a point and a line that are not incident, and with three non-colinear points. These cases are also solved as these two examples.

9. Intersection of two planes s2 a) s2 b) Q2 r2 Q2 q r2 Q2 x q Q1 Q2 x Q1 q r1 s1 Q1 Q1 q s1 r1 Q1 r1, Q1 s1 Q1= r1 s1 Q2 r2, Q2 s2 Q2= r2 s2 Remark. The horizontal projection of the intersection line coincides with the 1st trace of the plane (horizontal projection plane).

10. Solved exercises 1. Determine the traces of the plane which is parallel with the given plane P and contains the point T. m r2 T s2 M1 x s1 r1 m T M1

11. 2. Construct the traces of the plane which contains the point P and is parallel with lines a and b. r2 P2 p a q P b P1 x P2 Q1 a q Q1 r1 P p b P1 Remark. A line is parallel with a plane if it is parallel to any line of the plane. Instruction: Construct through the point P lines p and q so that p || b and q || a is valid.

12. 4. Construct the traces of the plane determined by the 3 non-colinear given points N2 3. Construct the traces of the plane determined by a given line and a point not lying on the line M2 r2 C m p n A T M r2 B m M2 M1 N2 x P2 x P1 C N1 M1 A P2 m P1 n m T M1 M s1 p M1 B r1 Instruction. Place a line throught the point T that intersect (or is parallel with) the line p. Here the chosen line is the vertical principle line. N1

13. 5. Detremine the 1st angle of inclination of the plane for which the line p is the 2nd steepest line of the plane. T2 s2 . P2 p P1 P2 x T2 p s1 1 To determine the 1st angle of inclination we can use any 1st steepest line t of that plane. T1 t T20 P1

14. 6. Determine the intersection of planes P and . z r2 s3t s1 t r3 s2 x y t r1 y

15. 7. Construct the plane throught the point T parallel with the symmetry plane. z s3 d3 s1 s2 k1 k2 T T T d1=d 2 y