Geometric Solids Volume Formulas Explained
Understanding the volume of geometric solids is crucial for various practical applications. Learn about different shapes like rectangular prisms, cylinders, cones, and spheres, along with their respective volume formulas. Dive into the concepts of diameter, radius, and height to master calculations for these three-dimensional figures.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Bell Ringer A farmer is trying to cross a river. He is taking with him a rabbit, carrots and a fox, and he has a small raft. He can only bring 1 item a time across the river because his raft can only fit either the rabbit, the carrots or the fox. How does he cross the river. (You can assume that the fox does not eat the rabbit if the man is present, you can also assume that the fox and the rabbit are not trying to escape and run away)
Volume of Solids Mr. Haupt CC.2.3.8.A.1
Volume Volume is how much space is inside a three dimensional shape. We can use this for a lot of stuff. How much water to put in a pool, and the amount of chemicals to put in. How much air to put into a tire. Etc. There are different formulas for each geometric solid.
Vocabulary Diameter The distance across a circle at its widest. Radius - Half of the diameter. Height The measurement from the base to the highest point and is perpendicular to the base.
Rectangular Prisms Rectangular prisms are six sided three dimensional solids. They look like boxes or cubes. The formula for finding volume is: Volume = Length x Width x Height V = L x W x H
Cylinders Cylinders are three dimensional solids that have two circles at the end and a quadrilateral wrapped around in between. They look like a soup can. The formula for finding volume is to find the area of the circle, and then multiply by the height. V = 3.14r2h
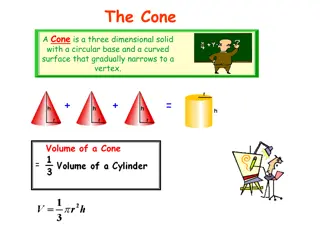
Cone Cones are three dimensional shapes that look like pyramids with a circular base. Look like ice cream cones, traffic cones, etc. Formula for volume is one third of pi times radius squared times the height. V = 1/3 (3.14) r2 h
Sphere A sphere is a hard to pronounce geometric solid that looks like a globe or a ball. The volume for this one is the hardest to remember, and is usually a bit of a pain. It is four thirds times pi times radius cubed. V = 4/3 (3.14) r3
