Congruent Triangles
Which shapes are
congruent
?
These triangles are
congruent
because all sides are of
equal length
SSS
We constructed SSS triangles in Year 7
Hypotenuse
In a right-angled triangle the longest side is called the hypotenuse.
It is always opposite the right angle.
These triangles are
congruent
because the sides of a
right-angled triangle are always in proportion. If we know
two sides we could calculate the third
(using Pythagoras Theorem
that we will learn about later this year
)
RHS
These triangles are
congruent
because if we know the
length & relative position of 2 sides there is only one
possibility for the third side.
SAS
We constructed ASA triangles in Year 7
These triangles are
congruent
because sides made using
angles at the end of an unknown length can only meet in
one place
ASA
We constructed
SAS
triangles in Year 7
Are these triangles
congruent
?
How do you know?
Are these triangles
congruent
?
How do you know?
No, not SAS because there are 3 triangles with these
possible dimensions
Are these triangles
congruent
?
How do you know?
Are these triangles
congruent
?
How do you know?
Are these triangles
congruent
?
How do you know?
The angles can be the same in different sized triangles
Congruent Triangles
Find the pairs of
congruent triangles
and state the reason
for congruency.
Every triangle has a
congruent triangle
Problem 1
Is triangle ADC congruent to triangle ABC?
Explain your answer
Problem 2
This shape is made from two triangles and four congruent parallelograms.
Are the triangles congruent?
Explain your reasoning.
In geometry, congruent triangles have equal sides and angles, leading to unique properties and relationships. By exploring the concepts of congruence in triangles, such as SSS (side-side-side), SAS (side-angle-side), ASA (angle-side-angle), and RHS (right-angle-hypotenuse-side), students develop a deep understanding of geometric principles. Through visual aids and explanations, the content emphasizes how knowing specific information about two sides or angles of a triangle allows for the determination of other related aspects, facilitating problem-solving and reasoning skills.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
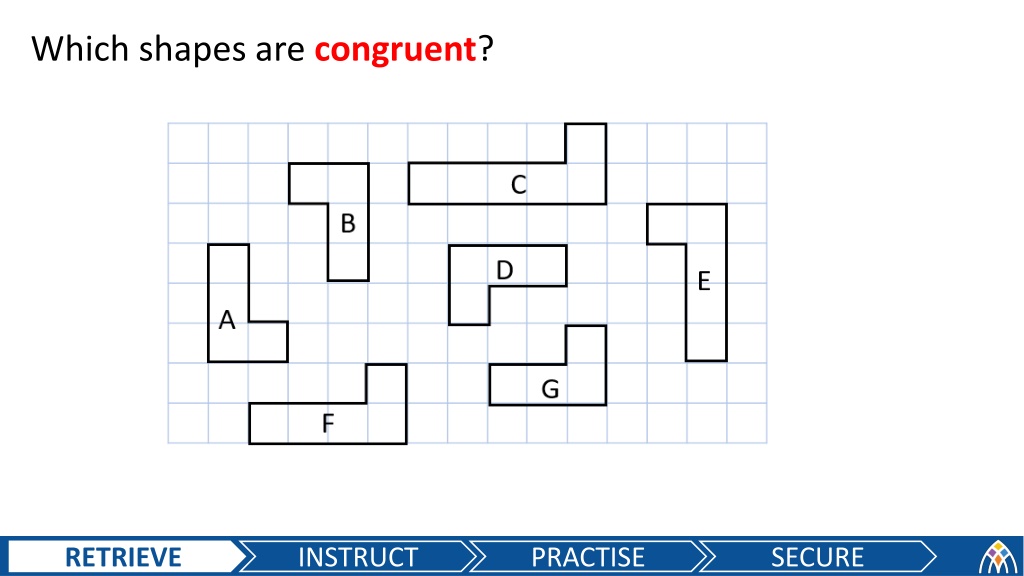
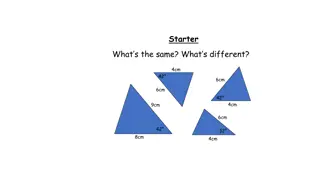
Which shapes are congruent? RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER These triangles are congruent because all sides are of equal length RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT SSS EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER We constructed SSS triangles in Year 7 RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Hypotenuse RETRIEVE In a right-angled triangle the longest side is called the hypotenuse. It is always opposite the right angle. DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER These triangles are congruent because the sides of a right-angled triangle are always in proportion. If we know two sides we could calculate the third (using Pythagoras Theorem that we will learn about later this year ) RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT RHS EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER These triangles are congruent because if we know the length & relative position of 2 sides there is only one possibility for the third side. RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT SAS EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER We constructed ASA triangles in Year 7 RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER These triangles are congruent because sides made using angles at the end of an unknown length can only meet in one place RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT ASA EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER We constructed SAS triangles in Year 7 RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Are these triangles congruent? How do you know? RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Are these triangles congruent? How do you know? RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER No, not SAS because there are 3 triangles with these possible dimensions RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Are these triangles congruent? How do you know? RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Are these triangles congruent? How do you know? RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Are these triangles congruent? How do you know? RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER The angles can be the same in different sized triangles RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Congruent Triangles RETRIEVE Find the pairs of congruent triangles and state the reason for congruency. DECODE CONNECT VISUALISE SUMMARISE Every triangle has a congruent triangle INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Problem 1 RETRIEVE Is triangle ADC congruent to triangle ABC? Explain your answer DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Problem 2 RETRIEVE This shape is made from two triangles and four congruent parallelograms. Are the triangles congruent? Explain your reasoning. DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
