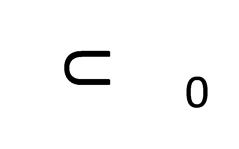Complex Increasing Sequence of Simplicial Complexes
http://link.springer.com/article/10.1007%2Fs00454-004-1146-y
a, b is in C
0
C
1
C
2
… C
5
{a, b, c} is in C4
C
5
http://link.springer.com/article/10.1007%2Fs00454-004-1146-y
Filtered complex from data points:
Filtered 1d-complex from data points:
Filtered Rips complex from data points:
Barcode for H
0
H
0
=
Z
0
/
B
0
=
cycles
boundaries
Barcode for H
1
H
1
=
Z
1
/
B
1
=
cycles
boundaries
Barcode for H
2
H
2
=
Z
2
/
B
2
=
cycles
boundaries
Computing Persistent Homology by Afra Zomorodian, Gunnar Carlsson
http://link.springer.com/article/10.1007%2Fs00454-004-1146-y
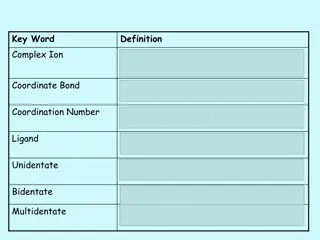
A filtered complex is an increasing sequence of simplicial complexes, denoted as C0, C1, C2. For more information, refer to the provided link.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
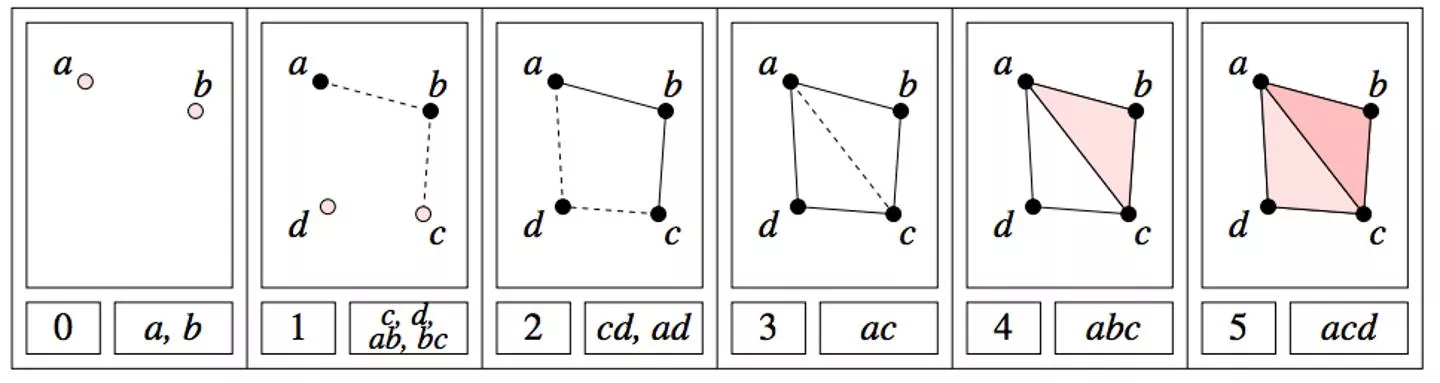
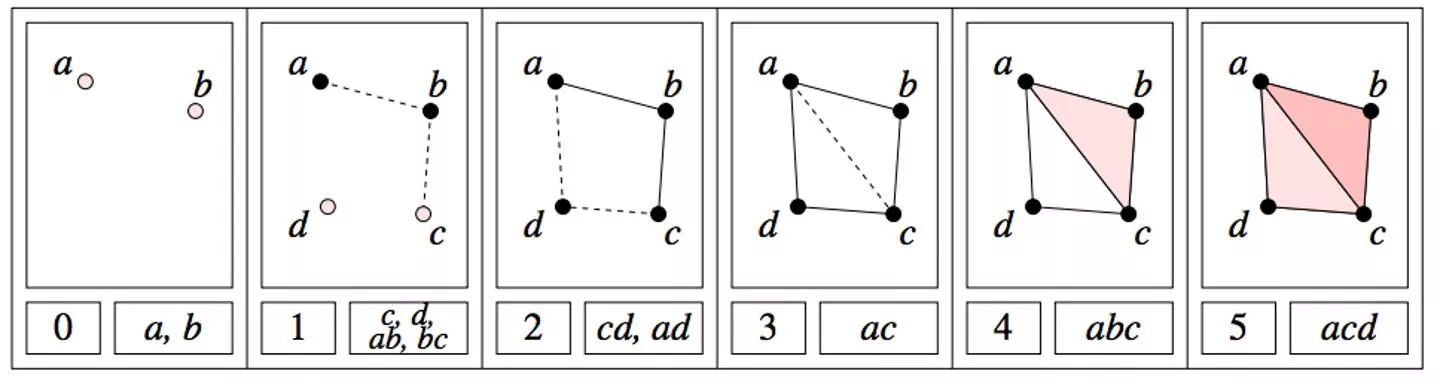
A filtered complex is an increasing sequence of simplicial complexes: C0 C1 C2 U U U http://link.springer.com/article/10.1007%2Fs00454-004-1146-y
A filtered complex is an increasing sequence of simplicial complexes: C0 C1 C2 U U U a, b is in C0 C1 C2 C5 0 0 U U U U 0 0 {a, b, c} is in C4 C5 U 2 2 http://link.springer.com/article/10.1007%2Fs00454-004-1146-y
A filtered complex is an increasing sequence of simplicial complexes: C0 C1 C2 U U U
Barcode for H0 H0 = Z0/B0 = cycles boundaries
Barcode for H1 H1 = Z1/B1 = cycles boundaries
Barcode for H2 H2 = Z2/B2 = cycles boundaries
Computing Persistent Homology by Afra Zomorodian, Gunnar Carlsson i, p Hk = Zk /(Bk Zk ) i i+p i U http://link.springer.com/article/10.1007%2Fs00454-004-1146-y
