Greedy Algorithms and Minimum Spanning Trees
Greedy algorithms build solutions by considering objects one at a time using simple rules, while Minimum Spanning Trees find the most cost-effective way to connect vertices in a weighted graph. Greedy algorithms can be powerful, but their correctness relies on subtle proofs and careful implementatio
7 views • 61 slides
Computational Geometry.
Voronoi diagrams, a key concept in computational geometry, involve partitioning a space based on points sites. They have diverse applications like nearest neighbor queries and facility location. The diagrams consist of Voronoi cells, edges, and vertices, forming a connected graph. Properties include
0 views • 19 slides
Breadth-First Search (BFS) Algorithm for Graph Searching
This content delves into the Breadth-First Search (BFS) algorithm, a fundamental graph searching technique. It explains the step-by-step process of BFS, from initializing the graph to traversing vertices in a specific order. Through detailed visual representations, you will gain insights into how BF
1 views • 75 slides
Explore 3D Shapes: Properties and Examples
Unveil the fascinating properties of 3D shapes through engaging visuals and descriptions. Identify shapes based on their faces, edges, vertices, and unique characteristics like curved faces or square-based structures.
0 views • 17 slides
Shapes and Their Properties
Explore the properties of 2D shapes such as sides, vertices, and unique characteristics through engaging visuals and descriptions. Learn about common shapes like circles, triangles, squares, rectangles, pentagons, hexagons, and heptagons. Enhance your understanding of geometry in a fun and interacti
1 views • 17 slides
Identifying Sides and Vertices in 2D Shapes for Year 2 Geometry Session
In this geometry lesson, we explore various 2D shapes such as square, triangle, circle, rectangle, pentagon, hexagon, heptagon, and octagon. We learn about the number of sides and vertices each shape has, distinguishing between shapes based on their unique characteristics.
2 views • 10 slides
Mastering 2-D Shape Vertices: Learning Guide
Understand the concept of vertices on 2-D shapes, learn how to count vertices, identify shapes based on their vertices, and determine the odd one out in a group of shapes. Explore the number of vertices in various shapes like a triangle, rectangle, pentagon, hexagon, octagon, and even a circle. Test
5 views • 16 slides
Polygon Clipping Techniques and Algorithms
Polygon clipping involves modifying line-clipping procedures to achieve bounded areas after clipping. The Sutherland-Hodgman algorithm is commonly used, where polygon boundaries are processed against window edges to generate closed areas for appropriate area fill. This process involves testing for v
1 views • 17 slides
Mastering Quadratic Functions: Graphing Through Transformations
Explore the vertex form of quadratic equations, understand transformation rules, and learn step-by-step methods for graphing quadratics with examples and practice problems. Enhance your skills in identifying vertices, plotting points, and visualizing the U-shaped graphs of quadratic functions.
0 views • 10 slides
Graph Connectivity and Single Element Recovery via Linear and OR Queries
The content discusses the concepts of graph connectivity and single element recovery using linear and OR queries. It delves into the strategies, algorithms, and tradeoffs involved in determining unknown vectors, edges incident to vertices, and spanning forests in graphs. The talk contrasts determini
0 views • 28 slides
GPolygon Class in Graphical Structures
The GPolygon class in graphical structures is utilized to represent graphical objects bounded by line segments, such as polygons. This class allows for the creation of polygons with vertices connected by edges, utilizing methods like addVertex and addEdge to construct the shape. The reference point
0 views • 26 slides
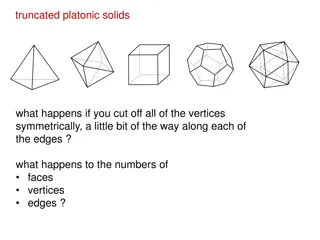
Exploring Truncated Platonic Solids and Polyhedra Patterns
Discover what happens when vertices are symmetrically cut off from Platonic solid shapes, leading to changes in the numbers of faces, vertices, and edges. Explore relationships between the original Platonic values and the truncated values, and investigate similar patterns in other polyhedra shapes.
0 views • 11 slides
Distributed Biconnectivity in Graph Analysis for Efficient Network Solutions
Graph biconnectivity is a crucial concept in network analysis, ensuring connectivity even when vertices are removed. Efficient distributed biconnectivity algorithms have practical applications in identifying single points of failure in networks. Leveraging previous work on Ice Sheet Connectivity, a
0 views • 35 slides
Quadratic Functions and Models: Characteristics and Equations
Explore writing quadratic functions given specific characteristics such as vertices, x-intercepts, and points passed through. Learn how to form equations in vertex form, intercept form, and standard form by plugging in values and solving systems of equations. Practice creating quadratic functions wi
0 views • 8 slides
FlashGraph: Processing Billion-Node Graphs on Commodity SSDs
FlashGraph proposes a system that combines SSDs and RAM for efficient graph processing, storing vertices in memory and edge lists in SSD storage. The system can handle large graphs without using excessive memory and boasts performance comparable to in-memory graph processing engines. While SSDs offe
0 views • 6 slides
Distributed Graph Coloring on Multiple GPUs: Advancements in Parallel Computation
This research introduces a groundbreaking distributed memory multi-GPU graph coloring implementation, achieving significant speedups and minimal color increase. The approach enables efficient coloring of large-scale graphs with billions of vertices and edges. Additionally, the study explores the pra
0 views • 22 slides
Exploring Triangles in Mathematics Class V
Dive into the world of triangles in Mathematics Class V as students learn to compare triangular shapes with other shapes, identify vertices, sides, and angles of a triangle, measure angles, find relations between angles and sides, solve word problems, and more. Engage in activities, implement knowle
0 views • 28 slides
Computation on Graphs: Maximal Independent Sets
The content discusses the concept of maximal independent sets in graph theory. It defines independent, maximal, and maximum sets, highlighting the difficulty in finding a maximum independent set due to its NP-hard nature. Sequential and parallel algorithms for finding maximal independent sets are pr
0 views • 12 slides
Structural Equivalence and Similarity Measures in Network Analysis
This content discusses the concepts of structural equivalence and regular equivalence in network analysis. Structural equivalence is based on shared network neighbors, while regular equivalence considers the similarities of neighboring vertices. Various measures, such as cosine similarity and Pearso
0 views • 12 slides
Balanced Graph Edge Partition and Its Practical Applications
Balanced graph edge partitioning is a crucial problem in graph computation, machine learning, and graph databases. It involves partitioning a graph's vertices or edges into balanced components while minimizing cut costs. This process is essential for various real-world applications such as iterative
1 views • 17 slides
Massively Parallel Algorithm for Minimum Weight Vertex Cover
Massively Parallel Computation (MPC) model for solving the Minimum Weight Vertex Cover problem efficiently, including optimal round complexities and known approximation ratios. The algorithm is designed for graphs with vertices and edges, with each machine processing data synchronously in rounds. Va
0 views • 13 slides
Innovations in Wireless PHY Programming for Hardware
Programming software radios is a key aspect of wireless communication research, with recent advancements in PHY/MAC design and the use of SDR platforms like GNURadio and SORA for experimentation. Challenges include FPGA limitations and the need for hardware synthesis platforms like ZIRIA for high-le
0 views • 41 slides
Trigonometry Basics for Robotics: Understanding Triangles and Interior Angle Addition
Explore the fundamentals of trigonometry in robotics through an in-depth look at triangles, their components, and the interior angle addition theorem. Learn about vertices, sides, angles, and the centroid of a triangle, as well as special right triangles. Enhance your understanding with detailed exa
0 views • 41 slides
Geometry in the Coordinate Plane
The content discusses various topics related to geometry in the coordinate plane, including finding points on a line that are a specific distance apart, classifying polygons by their sides, determining perimeters of polygons with given vertices, and calculating areas of triangles and polygons. It pr
0 views • 12 slides
Geometric Pipeline Implementation Strategies: From Vertices to Fragments
The chapter delves into the process of converting vertices into primitives, clipping out objects outside the view frustum, and determining affected pixels by each primitive. Tasks such as rasterization, transformations, hidden surface removal, and antialiasing are discussed. Various algorithms for c
0 views • 68 slides
Advanced Parcel Editing Techniques in ArcGIS
Explore the various tools and functionalities available within ArcGIS for cutting out parcels within a county database without relying on third-party software. Learn about options such as the Cogo Toolbar, Parcel Editor, and Parcel Fabric Toolbar, each offering unique capabilities like parcel splitt
0 views • 19 slides
Advanced Subpath Algorithms for Convex Hull Queries
This study presents innovative algorithms for subpath convex hull queries, focusing on efficient computation of convex hulls for subpaths between two vertices on a simple path in the plane. The work includes a comparison with previous methods, showcasing improvements in space complexity and query pr
0 views • 19 slides
Bounded Degree Polyhedronization of Point Sets in R3
The problem of finding a polyhedron in R3 with no four points coplanar, having the set of points as vertices, being simple in structure, with each vertex connected to O(1) edges, and featuring both a tetrahedralization and chain dual. This task has historical importance with Euler's formula setting
0 views • 24 slides
Symmetric Chromatic Function for Voltage Graphs
Exploring the concept of a Symmetric Chromatic Function (SCF) for voltage graphs involves proper coloring conditions for edges and vertices, edge polarization functions, and decomposing voltage graphs into disconnected and connected squiggly graphs. The SCF allows for determining the number of ways
0 views • 7 slides
Unraveling Time-Slices of Events in SPD Experiment at the 10th International Conference
In the context of the SPD experiment within the NICA project, the challenge lies in processing vast amounts of data efficiently to extract valuable events. The SPD experiment aims to study the spin structure of nucleons through polarized proton collisions. Approaches like predictive modeling, interp
0 views • 13 slides
Introduction to Creating Simplicial Complexes from Data
Learn how to create a simplicial complex from data points through a step-by-step process. Starting with 0-dimensional vertices and defining closeness between data points, progress to adding 1-dimensional edges. Ideal for those interested in topological data analysis across various fields.
0 views • 73 slides
Adjacency Labeling Schemes and Induced-Universal Graphs
Adjacency labeling schemes involve assigning L-bit labels to vertices in a graph for efficient edge determination. The concept of induced-universal graphs is explored, where a graph is universal for a family F if all graphs in F are subgraphs of it. Theorems and lower bounds related to adjacency lab
0 views • 24 slides
Learning 2D Shape Reflections with Grids and Vertices
Learn how to reflect 2D shapes using grids and vertices on a whiteboard. Understand vertical, horizontal, and diagonal reflections by plotting points, drawing lines, and reflecting shapes in this educational activity. Explore the symmetry across the line of reflection to grasp the concept visually.
0 views • 21 slides
Mastering Quadratic Functions in Algebra 2
Learn how to write equations, model data sets, and use quadratic regression in Algebra 2 through examples and practice problems. Explore writing equations using vertices, points, x-intercepts, and quadratic regression. Dive into applications like determining the height of a net where a clown lands a
0 views • 13 slides
Introduction to Computer Graphics and Multimedia Applications
This lecture covers the fundamentals of computer graphics and multimedia applications, focusing on quadric surfaces, polygon meshes, and different mesh representations such as explicit mesh, vertex pointer representation, and edge list representation. It explains how quadric surfaces are defined imp
0 views • 8 slides
Trees in Discrete Structures
Discrete Structures and Their Applications Trees Chapter discusses the properties and theorems related to trees in graph theory. Trees are defined as connected, undirected graphs with no cycles. The content covers the characteristics of leaves, internal vertices, and the relationship between the num
4 views • 28 slides
Basic Graph Terminology in Discrete Mathematics
Exploring the fundamental definitions in graph theory including adjacent vertices, neighborhoods, degrees of vertices, isolated and pendant vertices. Examples are provided to illustrate the concepts.
0 views • 25 slides
Depth-First Search Exploration Techniques
Depth-First Search (DFS) is a graph traversal algorithm that explores all edges leaving a vertex before backtracking. It continues until all reachable vertices are discovered. This process involves classifying edges as tree, back, forward, or cross edges based on the relationship between vertices. D
0 views • 22 slides
Directed Graphs and Adjacency Matrices in Discrete Structures
Explore the concepts of binary relations, directed graphs, adjacency matrices, transitive closure, and walks in the context of discrete structures. Learn how vertices, edges, in-degrees, out-degrees, and self-loops are defined in directed graphs. Understand the importance of adjacency matrices in re
1 views • 28 slides
Graphs in Mathematics and Computer Science
Graphs in mathematics and computer science are abstract data types used to represent relationships between objects. They consist of vertices connected by edges, which can be directed or undirected. Graphs find applications in various fields like electric circuits, networks, and transportation system
0 views • 19 slides