Mastering 2-D Shape Vertices: Learning Guide

Understand the concept of vertices on 2-D shapes, learn how to count vertices, identify shapes based on their vertices, and determine the odd one out in a group of shapes. Explore the number of vertices in various shapes like a triangle, rectangle, pentagon, hexagon, octagon, and even a circle. Test your knowledge with engaging exercises and explanations.

• 2-D Shapes
• Vertices
• Counting
• Geometry
• Learning

jaylah Follow

Uploaded on Jul 25, 2024 | 5 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

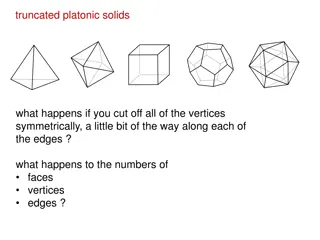
1. 4.2.21 WALT: Count the vertices on 2-D shapes Steps to success: I can understand the terms vertex and vertices I can explain what a vertex is. I can count vertices on a 2-D shape.

2. What is a vertex? On a 2D shape, a vertex is where two sides meet. A rectangle has 4 vertices.

3. Count the vertices on 2-D shapes Sort the shapes. Pentagon Hexagon Octagon

4. Count the vertices on 2-D shapes How many corners does a triangle have? When two lines meet at a point, we call it a vertex. vertex vertex vertex 3 A triangle has ____ vertices.

5. Count the vertices on 2-D shapes Where are the vertices on the rectangle? vertex vertex vertex vertex 4 A rectangle has ____ vertices.

6. Count the vertices on 2-D shapes How many vertices do these shapes have? 5 vertices 6 vertices 8 vertices

7. Count the vertices on 2-D shapes How many vertices are there on a circle? Can you explain why? 0 vertices because it only has one side and no points where 2 sides can meet.

8. Count the vertices on 2-D shapes I am thinking of a shape with 5 vertices. If it is a regular shape, which shape is it?

9. Count the vertices on 2-D shapes True or false? Can you prove it? To make 13 vertices in total, I need one more triangle. False. He needs one more pentagon.

10. Count the vertices on 2-D shapes Count the vertices. Which is the odd one out in each group?

11. Count the vertices on 2-D shapes Sort the shapes in the table. fewer than 5 vertices 5 or more vertices

12. Count the vertices on 2-D shapes

13. Count the vertices on 2-D shapes False. 4 + 3 makes 7 so you need 4 more vertices to make a total of 11. A triangle only has 3 vertices. You need another rectangle or a quadrilateral.

14. Count the vertices on 2-D shapes

15. Count the vertices on 2-D shapes B A E C F D A C B D E F

16. Count the vertices on 2-D shapes 3 6 0 4 5 4 4 8 7