Understanding Bernoulli's Equation in Fluid Mechanics
Bernoulli's equation, a fundamental principle in fluid dynamics, relates pressure, kinetic energy, and potential energy of a fluid flowing in a pipe. Through examples and explanations, explore how this equation can be used to calculate velocity, pressure differences, and forces in various scenarios
1 views • 12 slides
Overview of Army Modeling and Simulation Office
The U.S. Army Modeling and Simulation Office (AMSO) serves as the lead activity in developing strategy and policy for the Army Modeling and Simulation Enterprise. It focuses on effective governance, resource management, coordination across various community areas, and training the Army Analysis, Mod
1 views • 8 slides
Understanding Structural Equation Modeling (SEM) and Quality of Life Analysis
Structural Equation Modeling (SEM) is a statistical technique used to analyze relationships between variables, including quality of life factors such as physical health and mental well-being. Quality of life is a multidimensional concept encompassing various aspects like social relationships, living
0 views • 21 slides
Understanding Waveguiding Systems and Helmholtz Equation in Microwave Engineering
Waveguiding systems are essential in confining and channeling electromagnetic energy, with examples including rectangular and circular waveguides. The general notation for waveguiding systems involves wave propagation and transverse components. The Helmholtz Equation is a key concept in analyzing el
2 views • 50 slides
Understanding Thermodynamics and Fluid Mechanics Fundamentals for Efficiency
Explore key concepts in thermodynamics and fluid mechanics such as the equation of continuity, the first law of thermodynamics, the momentum equation, Euler's equation, and more. Learn about efficiency, internal energy, and the laws governing energy transfer in various systems. Delve into topics lik
2 views • 12 slides
Evolution of Modeling Methodologies in Telecommunication Standards
Workshop on joint efforts between IEEE 802 and ITU-T Study Group 15 focused on information modeling, data modeling, and system control in the realm of transport systems and equipment. The mandate covers technology architecture, function management, and modeling methodologies like UML to YANG generat
1 views • 16 slides
Understanding Geometric Modeling in CAD
Geometric modeling in computer-aided design (CAD) is crucially done in three key ways: wireframe modeling, surface modeling, and solid modeling. Wireframe modeling represents objects by their edges, whereas surface modeling uses surfaces, vertices, and edges to construct components like a box. Each
1 views • 37 slides
Understanding the Hammett Equation in Chemical Reactions
The Hammett equation explores how substituents influence the dissociation of benzoic acid, affecting its acidity. By quantifying this influence through a linear free energy relationship, the equation helps predict the impact of substituents on different processes. Through parameter definitions and m
0 views • 9 slides
Structural Analysis: The Woman in Black by Susan Hill
In this structural analysis, key subject terminology and structural features are explored to understand how writers use these elements to achieve effects and influence readers. The focus is on a specific extract from The Woman in Black by Susan Hill, analyzing how the author utilizes structural feat
0 views • 8 slides
Introduction to Dynamic Structural Equation Modeling for Intensive Longitudinal Data
Dynamic Structural Equation Modeling (DSEM) is a powerful analytical tool used to analyze intensive longitudinal data, combining multilevel modeling, time series modeling, structural equation modeling, and time-varying effects modeling. By modeling correlations and changes over time at both individu
0 views • 22 slides
Understanding Separation Columns in Chemical Engineering
Explore the world of separation columns including distillation, absorption, and extraction, along with empirical correlations, minimum number of stages, Fenske equation, Underwood equation, Kirkbride equation, examples, and solutions presented by Dr. Kh. Nasrifar from the Department of Chemical and
5 views • 15 slides
Analysis of Structural Transformation Trends in the Nigerian Economy
Economic development entails growth accompanied by structural change and technological advancement. This analysis delves into the patterns and trends of structural transformation in the Nigerian economy as discussed by Prof. Olu Ajakaiye, Executive Chairman of the African Centre for Shared Developme
0 views • 25 slides
Comprehensive Overview of Freezing Time Methods in Dairy Engineering
Neumann, Tao, and Non-Dimensional methods are key approaches for determining freezing times in unsteady state heat transfer processes in dairy engineering. The Neumann Problem, Tao Solutions, and Cleland and Earle Non-Dimensional Equation offer distinct equations and models to calculate freezing tim
1 views • 8 slides
System Modeling and Simulation Overview
This content provides insights into CPSC 531: System Modeling and Simulation course, covering topics such as performance evaluation, simulation modeling, and terminology in system modeling. It emphasizes the importance of developing simulation programs, advantages of simulation, and key concepts lik
0 views • 28 slides
Understanding Object Modeling in Software Development
Object modeling is a crucial concept in software development, capturing the static structure of a system by depicting objects, their relationships, attributes, and operations. This modeling method aids in demonstrating systems to stakeholders and promotes a deeper understanding of real-world entitie
1 views • 65 slides
Structural Analysis and Design for Signal and Lighting Systems
Florence Hutcheson Lee Sewell, PE, SE conducted an in-depth structural analysis known as SALSA to examine wire span, mast arm, and high mast structures. This comprehensive study, initiated in 2007, aimed to enhance the geotechnical evaluations of pole bases to meet current standards. Through innovat
2 views • 18 slides
Introduction to Quantum Mechanics: Energy Levels and Schrödinger Equation
Quantum mechanics reveals that all systems possess discrete energy levels, determined by solving the Schrödinger equation where the Hamiltonian operator represents total energy. In a particle-in-a-box scenario, potential energy is infinite outside the box. The Schrödinger equation simplifies to a
0 views • 12 slides
Coupled Ocean-Atmosphere Modeling on Icosahedral Grids
Coupled ocean-atmosphere modeling on horizontally icosahedral and vertically hybrid-isentropic/isopycnic grids is a cutting-edge approach to modeling climate variability. The design goals aim to achieve a global domain with no grid mismatch at the ocean-atmosphere interface, with key indicators such
1 views • 21 slides
Fundamental Comparison: Wheeler-DeWitt vs. Schrödinger Equation
The debate on whether the Wheeler-DeWitt equation is more fundamental than the Schrödinger equation in quantum gravity remains inconclusive. While the Wheeler-DeWitt equation presents an elegant formulation, the Schrödinger equation is essential in specific cases. The issue of time and coordinate
0 views • 6 slides
Understanding Open Channel Flow and Mannings Equation
This review covers hydraulic devices such as orifices, weirs, sluice gates, siphons, and outlets for detention structures. It focuses on open channel flow, including uniform flow and varied flow, and explains how to use Mannings equation for calculations related to water depth, flow area, and veloci
1 views • 43 slides
Exploring Membrane Potential Densities and the Fokker-Planck Equation in Neural Networks
Delve into the concepts of membrane potential densities and the Fokker-Planck Equation in neural networks, covering topics such as integrate-and-fire with stochastic spike arrival, continuity equation for membrane potential density, jump and drift flux, and the intriguing Fokker-Planck Equation.
0 views • 29 slides
Structural Equivalence and Similarity Measures in Network Analysis
This content discusses the concepts of structural equivalence and regular equivalence in network analysis. Structural equivalence is based on shared network neighbors, while regular equivalence considers the similarities of neighboring vertices. Various measures, such as cosine similarity and Pearso
0 views • 12 slides
Advancing Computational Modeling for National Security and Climate Missions
Irina Tezaur leads the Quantitative Modeling & Analysis Department, focusing on computational modeling and simulation of complex multi-scale, multi-physics problems. Her work benefits DOE nuclear weapons, national security, and climate missions. By employing innovative techniques like model order re
0 views • 6 slides
Leapfrog Scheme for Advection Equation
The provided images illustrate the Leapfrog scheme applied to an advection equation, focusing on the center method in time and space. The stability of the method is analyzed with assumptions regarding the behavior of the solution. Through the exploration of Courant numbers and CFL conditions, the st
0 views • 25 slides
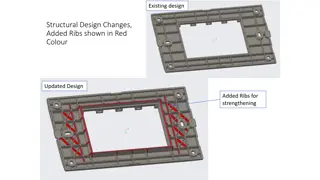
Structural Design Enhancement with Added Ribs for Strength
Discover the updated structural design featuring added ribs highlighted in red for enhanced strength and stability. Witness the transformation from the existing design to the reinforced version through detailed stress analysis. The innovative changes showcase a significant improvement in the structu
0 views • 4 slides
Understanding Hardware Design Languages in Advanced Computer Architecture
This material covers topics like behavioral correctness, timing simulations, domains, and levels of modeling in hardware design languages. It discusses functional and structural modeling, as well as the use of simulators to analyze and verify system behavior. Hardware Design Languages, behavioral de
0 views • 38 slides
Excel Tutorial: Finding Trendline Equation and Calculating Rates of Change
Learn how to find the equation of a trendline in Excel and use it to calculate rates of change. This step-by-step guide includes importing data, adding a trendline, displaying the equation, and interpreting it for analysis. Make the most of Excel's features for data analysis.
0 views • 11 slides
Understanding Modal Testing and Analysis in Structural Dynamics
Modal testing and analysis play a crucial role in understanding the behavior of structural systems under various conditions like undamped, viscously damped, and hysterically damped scenarios. This analysis involves the study of single-degree-of-freedom systems, undamped systems for free and forced v
0 views • 23 slides
Linearized Boltzmann Equation in Statistical Mechanics
This lecture delves into the linearized Boltzmann equation and its applications in studying transport coefficients. The content covers the systematic approximation of transport coefficients, impact parameters of collisions, and the detailed solution for a dilute gas system. It explores the notation
0 views • 25 slides
Quantum Chemistry Learning Goals and Concepts
This content covers the learning goals and concepts of quantum chemistry leading up to the Schrodinger equation and potential energy wells, excluding the material on the hydrogen atom introduced later. It explores models of the atom, including observations of atomic spectra, the Bohr model, de Brogl
0 views • 22 slides
Importance of Data Modeling in Industrial Information Systems
Introduction to data modeling and design in Industrial Information Systems at King Saud University College of Engineering. The chapter covers the significance of data modeling, capturing data characteristics, structural information, and the role of databases and DBMS. Data modeling fills crucial gap
0 views • 51 slides
Analytical Solutions for 2D Heat Equation with Separation of Variables
Consider the steady-state 2D heat equation with constant thermal conductivity. Analyze analytical solutions using separation of variables method for a square plate with defined boundary conditions. Learn how to express the general form of solutions and apply them to the heat equation in Cartesian ge
0 views • 15 slides
Understanding Structural Identification in Vector Autoregressions
Explore the algebra of identification problems in VARs, including Cholesky factorization, timing restrictions, long-run impact restrictions, sign restrictions, and identification through heteroskedasticity. Discover why structural identification is crucial for policy design, economic modeling, and u
0 views • 63 slides
Understanding System Modeling in Software Engineering
System modeling in software engineering involves developing abstract models of a system to understand its functionality and communicate with stakeholders. Models are used in requirements engineering, design proposals, and system documentation. Different perspectives like external, structural, intera
0 views • 35 slides
Dynamic Function for Basal Area of Trees Derived from Differential Equation
Mathematical methods presented by Braun and Simmons are used to derive a dynamic function for the basal area of individual trees from a production-theoretically motivated autonomous differential equation. The differential equation and general dynamic function are described, highlighting the relation
0 views • 45 slides
NetLogo - Programmable Modeling Environment for Simulating Natural and Social Phenomena
NetLogo is a powerful and versatile programmable modeling environment created by Uri Wilensky in 1999. It allows users to simulate natural and social phenomena by giving instructions to multiple agents operating independently, making it ideal for modeling complex systems evolving over time. NetLogo
0 views • 7 slides
Male/Female Handwashing Behaviors During A(H1N1) Pandemic: A Structural Equation Modeling Study
This study by PhD Benicio Gutiérrez explores male and female handwashing behaviors during the A(H1N1) pandemic of 2009-2010 using Structural Equation Modeling. The research focuses on understanding the motivations behind handwashing practices during the pandemic, emphasizing the importance of prope
0 views • 14 slides
Analysis and Comparison of Wave Equation Prediction for Propagating Waves
Initial analysis and comparison of the wave equation and asymptotic prediction of a receiver experiment at depth for one-way propagating waves. The study examines the amplitude and information derived from a wave equation migration algorithm and its asymptotic form. The focus is on the prediction of
0 views • 23 slides
Understanding the Photoelectric Effect and Einstein's Equation
The photoelectric effect is explained by Einstein through assumptions of photons and their interaction with electrons on a metal surface. The maximum kinetic energy of ejected electrons depends on the frequency of incident radiation, as shown in Einstein's Equation. The greater the frequency, the hi
0 views • 6 slides
Graphical Solution of Equations Using GDC - Step-by-Step Guide
Learn how to solve equations graphically using a Graphic Display Calculator (GDC) with step-by-step instructions. Turn on the GDC, input the equation on Y1 and Y2, draw the graphs, and find the intersection point to determine the x-value. An example equation, 2x + 8 = x + 1, is solved using this met
0 views • 20 slides