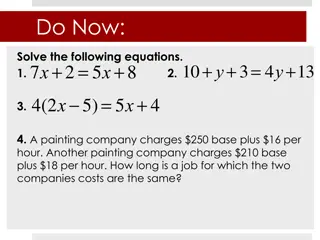Understanding Chemical Reactions: Reactants, Products, and Balancing Equations
Chemical reactions involve reactants that transform into products. Balancing equations is essential to ensure the conservation of mass. Learn about decomposition reactions, chemical equations, and methods to balance equations effectively.
4 views • 39 slides
Stochastic Storm Transposition in HEC-HMS: Modern Techniques and Applications
Explore the innovative methods and practical applications of Stochastic Storm Transposition (SST) in the context of HEC-HMS. Delve into the history, fundamentals, simulation procedures, and benefits of using SST for watershed-averaged precipitation frequency analysis. Learn about the non-parametric
3 views • 41 slides
Understanding Numerical Methods for Approximating Analytic Equations
Introduction to approximating solutions to analytic equations, focusing on differential equations, integral equations, and integro-differential equations. Exploring ordinary and partial derivatives, differential and integral equations, and the involvement of unknown functions and their derivatives a
2 views • 15 slides
Equations of State in Thermodynamics
In the study of thermodynamics, equations of state play a crucial role in predicting the behavior of substances based on pressure, volume, and temperature relationships. These equations define the interdependence of various intensive properties for a simple compressible substance. The development an
0 views • 42 slides
Understanding Maxwell Equations in Thermodynamics
In thermodynamics, Maxwell equations are derived using Euler's reciprocity relation. They involve characteristic functions such as internal energy, free energy, enthalpy, and Gibbs free energy, along with parameters like temperature, entropy, pressure, and volume. These equations form the foundation
0 views • 15 slides
Differential Equations of First Order & Higher Degree: Lecture 18
This lecture covers differential equations of first order but not of the first degree, general forms of such equations, methods for solving them, and examples of differential equations to be solved. The content includes detailed explanations, equations, solutions, and problem-solving techniques.
0 views • 9 slides
Understanding Linear Equations in Algebra: A Comprehensive Overview
An exploration of algebraic expressions, equations, and linear equations in one variable with detailed explanations and examples. Discover the fundamental concepts, solving methods, and applications of linear equations in various word problems. Master the art of transforming mathematical expressions
0 views • 15 slides
Linear Equations Checkpoint Activities for Year 8 Students
This diagnostic mathematics resource for Year 8 students focuses on solving linear equations through a series of Checkpoint and additional activities. Published in 2021/22, the content covers topics such as representing equations with algebra and solving for unknown variables. Students will engage w
0 views • 47 slides
Learning Linear Equations in Two Variables
Understanding linear equations in two variables is essential for solving real-life problems. This topic covers the definition, solution, and graphical representation of such equations, helping students connect mathematical concepts to practical scenarios. By learning to write and solve linear equati
3 views • 31 slides
Understanding Graphs of Straight Lines and Equations
Learn how to graph equations and find equations from graphs of straight lines. Explore tables of values, plotting points on a coordinate plane, drawing lines through points, and identifying relationships between graphs and algebraic expressions. Discover the gradient-intercept form of a straight lin
0 views • 14 slides
Understanding Differential Equations: Types, Classification, and Solutions
Differential equations are mathematical equations that relate independent and dependent variables through differential coefficients. They can be classified as ordinary or partial, based on the types of derivatives involved. The order and degree of a differential equation, as well as its linearity an
2 views • 26 slides
Understanding Differential Equations in Economics Honours
Differential equations, introduced by Newton and Leibniz in the 17th century, play a key role in economics. These equations involve derivatives and represent implicit functional relationships between variables and their differentials, often related to time functions. The order and degree of a differ
1 views • 16 slides
Introduction to Differential Equations and Laplace Equations
Understanding differential equations of various orders, solving methods, linear and non-linear equations, ordinary and partial differential equations, definitions of solutions, and general vs. particular solutions in the context of Differential Equations and Laplace Equations.
1 views • 20 slides
Understanding Differential Equations: Basics to Applications
Differential equations are fundamental in mathematics, with various types such as first-order, partial, and Clairaut's equations explored in this content. The content covers general equations, solutions, and examples, providing insights into linear and higher-order equations with constant coefficien
0 views • 20 slides
Understanding Partial Differential Equations of Second Order
Exploring the concepts of second-order partial differential equations in mathematics, including the general form, linear equations with variable coefficients, and equations with constant coefficients. Learn about integral solutions, examples, and techniques for solving these equations with detailed
0 views • 21 slides
Panel Stochastic Frontier Models with Endogeneity in Stata
Introducing xtsfkk, a new Stata command for fitting panel stochastic frontier models with endogeneity, offering better control for endogenous variables in the frontier and/or the inefficiency term in longitudinal settings compared to standard estimators. Learn about the significance of stochastic fr
0 views • 13 slides
Generalization of Empirical Risk Minimization in Stochastic Convex Optimization by Vitaly Feldman
This study delves into the generalization of Empirical Risk Minimization (ERM) in stochastic convex optimization, focusing on minimizing true objective functions while considering generalization errors. It explores the application of ERM in machine learning and statistics, particularly in supervised
0 views • 11 slides
Solving Exponential Equations Algebraically
Learn how to solve exponential equations algebraically with the same base and unlike bases. Understand the properties of equality for exponential equations and practice solving various equations step by step. Improve your skills in rewriting equations with the same base and applying the rules of exp
0 views • 9 slides
Understanding Matrices and Solving Equations in Electrical Engineering
Matrices play a crucial role in solving linear equations in Electrical Engineering applications. Learn about matrix structures, special matrices, inverses, transposes, system of linear equations, and solving methods using MATLAB/Python. Explore the application of matrices in solving voltage-current
1 views • 24 slides
Understanding Linear Equations in Two Variables
Explore linear equations in two variables, solving systems of equations, graphing solutions, and determining types of solutions. Learn how to analyze and find solutions graphically, identify infinite solutions, no solutions, and unique solutions, and understand the concept of dependent systems. Disc
0 views • 35 slides
Stochastic Coastal Regional Uncertainty Modelling II (SCRUM2) Overview
SCRUM2 project aims to enhance CMEMS through regional/coastal ocean-biogeochemical uncertainty modelling, ensemble consistency verification, probabilistic forecasting, and data assimilation. The research team plans to contribute significant advancements in ensemble techniques and reliability assessm
0 views • 28 slides
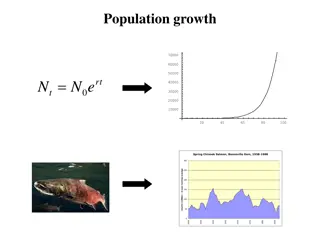
Understanding Population Growth Models and Stochastic Effects
Explore the simplest model of population growth and the assumptions it relies on. Delve into the challenges of real-world scenarios, such as stochastic effects caused by demographic and environmental variations in birth and death rates. Learn how these factors impact predictions and models.
0 views • 35 slides
Completing the Square Method: Vertex Form and Solving Equations
The Completing the Square method helps convert quadratic equations from standard form to vertex form, facilitating the quick determination of the vertex point and the solutions without factoring. By completing the square, you transform equations like y = x^2 + bx + c into y = (x − h)^2 + k, enabli
0 views • 5 slides
GCSE Algebra Revision Materials and Equations Practice
Explore a collection of GCSE algebra revision materials, including solving linear equations and common mishaps in algebraic simplification. Practice setting up equations and solving linear equations with provided examples and questions. Enhance your algebra skills through comprehensive content desig
0 views • 15 slides
Understanding Jeans Equations in Stellar Dynamics
The Jeans Equations and Collisionless Boltzmann Equation play a crucial role in describing the distribution of stars in a gravitational potential. By applying assumptions like axial symmetry and spherical symmetry, these equations provide insights into the behavior of large systems of stars. Despite
0 views • 7 slides
Understanding Linear Equations and Relationships
Explore various questions related to linear equations, slopes, y-intercepts, proportional relationships, and unit rates with step-by-step solutions and explanations. Practice identifying linear functions and graphing equations through real-life scenarios. Enhance your understanding of slope-intercep
0 views • 16 slides
Applications of Differential Equations in Engineering and Mathematics
Exploring the practical applications of differential equations, specifically focusing on Newton's Law of Cooling and Orthogonal Trajectories. The concept of exact differential equations and their solutions, along with real-life examples demonstrating temperature changes over time, are discussed. Und
0 views • 11 slides
Multiserver Stochastic Scheduling Analysis
This presentation delves into the analysis and optimality of multiserver stochastic scheduling, focusing on the theory of large-scale computing systems, queueing theory, and prior work on single-server and multiserver scheduling. It explores optimizing response time and resource efficiency in modern
0 views • 38 slides
Approximation Algorithms for Stochastic Optimization: An Overview
This piece discusses approximation algorithms for stochastic optimization problems, focusing on modeling uncertainty in inputs, adapting to stochastic predictions, and exploring different optimization themes. It covers topics such as weakening the adversary in online stochastic optimization, two-sta
0 views • 33 slides
Equations and Painting Costs Analysis
In this lesson, students will solve equations involving variables on both sides to determine the number of solutions. Additionally, a comparison is made between two painting companies based on their pricing structures to find the point where their costs are equal. Various examples and concepts relat
0 views • 12 slides
Optimal Sustainable Control of Forest Sector with Stochastic Dynamic Programming and Markov Chains
Stochastic dynamic programming with Markov chains is used for optimal control of the forest sector, focusing on continuous cover forestry. This approach optimizes forest industry production, harvest levels, and logistic solutions based on market conditions. The method involves solving quadratic prog
0 views • 27 slides
Integrating Stochastic Weather Generator with Climate Change Projections for Water Resource Analysis
Exploring the use of a stochastic weather generator combined with downscaled General Circulation Models for climate change analysis in the California Department of Water Resources. The presentation outlines the motivation, weather-regime based generator description, scenario generation, and a case s
0 views • 20 slides
Understanding Stochastic Differential Equations and Numerical Integration
Explore the concepts of Brownian motion, integration of stochastic differential equations, and derivations by Einstein and Langevin. Learn about the assumptions, forces, and numerical integration methods in the context of stochastic processes. Discover the key results and equations that characterize
0 views • 6 slides
Introduction to Generalized Stochastic Petri Nets (GSPN) in Manufacturing Systems
Explore Generalized Stochastic Petri Nets (GSPN) to model manufacturing systems and evaluate steady-state performances. Learn about stochastic Petri nets, inhibitors, priorities, and their applications through examples. Delve into models of unreliable machines, productions systems with priorities, a
0 views • 44 slides
Exploring Stochastic Algorithms: Monte Carlo and Las Vegas Variations
Stochastic algorithms, including Monte Carlo and Las Vegas variations, leverage randomness to tackle complex tasks efficiently. While Monte Carlo algorithms prioritize speed with some margin of error, Las Vegas algorithms guarantee accuracy but with variable runtime. They play a vital role in primal
0 views • 13 slides
Optimal Early Drought Detection Using Stochastic Process
Explore an optimal stopping approach for early drought detection, focusing on setting trigger levels based on precipitation measures. The goal is to determine the best time to send humanitarian aid by maximizing expected rewards and minimizing expected costs through suitable gain/risk functions. Tas
0 views • 4 slides
Optimizing User Behavior in Viral Marketing Using Stochastic Control
Explore the world of viral marketing and user behavior optimization through stochastic optimal control in the realm of human-centered machine learning. Discover strategies to maximize user activity in social networks by steering behaviors and understanding endogenous and exogenous events. Dive into
0 views • 15 slides
Understanding Tradeoff between Sample and Space Complexity in Stochastic Streams
Explore the relationship between sample and space complexity in stochastic streams to estimate distribution properties and solve various problems. The research delves into the tradeoff between the number of samples required to solve a problem and the space needed for the algorithm, covering topics s
0 views • 23 slides
Efficient Training of Dense Linear Models on FPGA with Low-Precision Data
Training dense linear models on FPGA with low-precision data offers increased hardware efficiency while maintaining statistical efficiency. This approach leverages stochastic rounding and multivariate trade-offs to optimize performance in machine learning tasks, particularly using Stochastic Gradien
0 views • 26 slides
Understanding Fixpoint Equations in Programming Languages
Fixpoint equations play a crucial role in programming languages for solving mutually recursive problems like parsing and dataflow analysis. This content explores the concepts of fixpoint equations, assumptions for ensuring solutions, computing solutions, and generalizations for cases with greatest e
0 views • 31 slides