Mathematics Course Selection Guide for Fall Semester
Academic advisors Olivia Biehle, Nathaniel Sulapas, and Jennifer McHam at the University of Texas provide guidance on selecting mathematics courses for the fall semester. The guide includes information on course sequences, considerations based on UTMA scores, AP credit recommendations, dual credit o
3 views • 20 slides
Understanding Dental Calculus Formation and Classification
Dental calculus, also known as tartar, is a mineralized bacterial plaque that forms on natural teeth and dental prostheses. It can be classified as supragingival or subgingival based on its relation to the gingival margin. This hard deposit is formed through the mineralization of dental plaque and c
5 views • 36 slides
Stochastic Storm Transposition in HEC-HMS: Modern Techniques and Applications
Explore the innovative methods and practical applications of Stochastic Storm Transposition (SST) in the context of HEC-HMS. Delve into the history, fundamentals, simulation procedures, and benefits of using SST for watershed-averaged precipitation frequency analysis. Learn about the non-parametric
3 views • 41 slides
AQA Level 2 Certificate in Further Maths
The AQA Level 2 Certificate in Further Maths is designed for high-achieving students to develop advanced skills in algebra, geometry, calculus, matrices, trigonometry, functions, and graphs. The course covers topics like number fractions, decimals, algebraic fractions, coordinate geometry, calculus,
7 views • 9 slides
Understanding Integral Calculus: Two Major Approaches & Antiderivatives
In this chapter, we delve into the fundamental concepts of integral calculus, focusing on two major approaches to mathematically generate integrals and assigning physical meanings to them. We explore antiderivatives, differentiation, integration, and the process of taking integration as the inverse
2 views • 59 slides
Understanding Related Rates and Differentials in Calculus
Derivatives involve very small changes in variables, leading to differentials. Related rates in calculus help us find how variables change in relation to each other. Learn how to solve related rates problems step by step with examples involving volumes, radii, and rates of change.
0 views • 11 slides
Understanding Classical Mechanics: Variational Principle and Applications
Classical Mechanics explores the Variational Principle in the calculus of variations, offering a method to determine maximum values of quantities dependent on functions. This principle, rooted in the wave function, aids in finding parameter values such as expectation values independently of the coor
0 views • 16 slides
Understanding the Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus states that if a function is continuous on an interval and has an antiderivative on that interval, then the integral of the function over the interval is equal to the difference of the antiderivative evaluated at the endpoints. This concept is further explored thr
0 views • 14 slides
Integrating Reverse Chain Rule and Substitution in Calculus
Explore the concepts of reverse chain rule and substitution in integration through worked examples and practice questions involving trigonometric functions. Enhance your skills with interactive narration and practical exercises. Dive into the world of calculus with a silent teacher guiding you throu
0 views • 5 slides
Understanding Points of Inflection in Calculus
Points of inflection in calculus refer to points where the curve changes from convex to concave or vice versa. These points are identified by observing changes in the curve's concavity, and they are not always stationary points. A stationary point can be a point of inflection, but not all points of
0 views • 14 slides
Understanding Accumulation Problems and Definite Integrals in Applied Calculus
Explore the interpretation of definite integrals in accumulation problems, where rates of change are accumulated over time. Learn how to solve accumulation problems using definite integrals and avoid common mistakes by understanding when to use initial conditions. Discover the relation between deriv
0 views • 9 slides
Understanding Rates of Change and Calculus Concepts
Exploring the concept of rates of change through examples like finding the equation of a line passing through given points and understanding differentiation to calculate gradients and speeds. The relationship between gradients, curves, and tangents is highlighted to illustrate how calculus helps in
1 views • 21 slides
Calculus Examples and Practice
Explore various calculus problems involving finding gradients, equations of tangents and normals, and analyzing curves. Practice determining gradients at specific points, solving for coordinates, and differentiating equations to find tangent and normal lines. Understand the relationship between grad
1 views • 11 slides
Overview of Vector Calculus for ECE 3317 Course
This overview provides a brief explanation of vector calculus concepts essential for the ECE 3317 course on Applied Electromagnetic Waves. It covers del operator, gradient, divergence, curl, vector Laplacian, vector identities, and their applications in electromagnetic field theory.
0 views • 24 slides
Panel Stochastic Frontier Models with Endogeneity in Stata
Introducing xtsfkk, a new Stata command for fitting panel stochastic frontier models with endogeneity, offering better control for endogenous variables in the frontier and/or the inefficiency term in longitudinal settings compared to standard estimators. Learn about the significance of stochastic fr
0 views • 13 slides
Generalization of Empirical Risk Minimization in Stochastic Convex Optimization by Vitaly Feldman
This study delves into the generalization of Empirical Risk Minimization (ERM) in stochastic convex optimization, focusing on minimizing true objective functions while considering generalization errors. It explores the application of ERM in machine learning and statistics, particularly in supervised
0 views • 11 slides
Techniques of Integration in Calculus II
Explore various techniques of integration in Calculus II such as basic integration formulas, simplifying substitutions, completing the square, expanding powers with trigonometric identities, and eliminating square roots. Examples and solutions are provided to help understand these integration method
0 views • 8 slides
Understanding Formal Semantics of Programming Languages: From Lambda Calculus to Separation Logic
Explore the foundational concepts of formal semantics in programming languages, covering Lambda Calculus, Untyped and Simply-typed languages, Imperative languages, Operational and Hoare logics, as well as Separation logic. Delve into syntax, reduction rules, typing rules, and operational semantics i
7 views • 14 slides
Understanding Continuity and Differentiability in Calculus
This module covers the concepts of continuity and differentiability in calculus, including the definition of derivatives, differentiability criteria, the Chain Rule, and derivatives of implicit functions. The content discusses the relationship between continuity and differentiability, previous knowl
0 views • 12 slides
Understanding Geometric Algebra and Calculus: A Deep Dive into Vector Derivatives and Maxwell Equations
Explore the world of geometric algebra and calculus through topics such as vector derivatives, Cauchy-Riemann equations, Maxwell equations, and spacetime physics. Unify diverse mathematical concepts to gain insights into analytic functions, differential operators, and directed integration.
0 views • 20 slides
Understanding Rolle's Mean Value Theorem in Calculus
Rolle's Mean Value Theorem states that if a function is continuous in a closed interval, differentiable in the open interval, and the function values at the endpoints of the interval are equal, then there exists at least one point where the derivative of the function is zero. This theorem is verifie
0 views • 11 slides
Understanding Predicate Calculus: Symbols, Terms, and Variables
Predicate calculus extends propositional calculus by introducing symbols like truth values, constants, variables, and functions. It allows for precise manipulation of components within assertions, enabling the creation of general statements about classes of entities. Learn how predicates define rela
1 views • 14 slides
Stochastic Coastal Regional Uncertainty Modelling II (SCRUM2) Overview
SCRUM2 project aims to enhance CMEMS through regional/coastal ocean-biogeochemical uncertainty modelling, ensemble consistency verification, probabilistic forecasting, and data assimilation. The research team plans to contribute significant advancements in ensemble techniques and reliability assessm
0 views • 28 slides
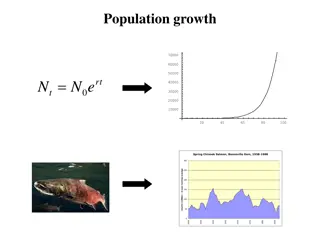
Understanding Population Growth Models and Stochastic Effects
Explore the simplest model of population growth and the assumptions it relies on. Delve into the challenges of real-world scenarios, such as stochastic effects caused by demographic and environmental variations in birth and death rates. Learn how these factors impact predictions and models.
0 views • 35 slides
Multiserver Stochastic Scheduling Analysis
This presentation delves into the analysis and optimality of multiserver stochastic scheduling, focusing on the theory of large-scale computing systems, queueing theory, and prior work on single-server and multiserver scheduling. It explores optimizing response time and resource efficiency in modern
0 views • 38 slides
Approximation Algorithms for Stochastic Optimization: An Overview
This piece discusses approximation algorithms for stochastic optimization problems, focusing on modeling uncertainty in inputs, adapting to stochastic predictions, and exploring different optimization themes. It covers topics such as weakening the adversary in online stochastic optimization, two-sta
0 views • 33 slides
Applications of Calculus in Optimization Problems
Calculus plays a crucial role in solving optimization problems to find maximum or minimum values in various real-life scenarios. This content provides examples of optimizing for maximum profit, area, distance, and volume using calculus concepts. From finding optimal dimensions for fencing to maximiz
0 views • 10 slides
Understanding Calculus: From MVT to FTC with Lin McMullin
Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m
0 views • 45 slides
Understanding the Fundamental Theorem of Calculus
Explore the connection between differential calculus and the definite integral through the fundamental theorem of calculus, which allows for the evaluation of complex summations. Discover the properties of definite integrals and how to apply the theorem to find areas under curves. Practice evaluatin
0 views • 15 slides
Optimal Sustainable Control of Forest Sector with Stochastic Dynamic Programming and Markov Chains
Stochastic dynamic programming with Markov chains is used for optimal control of the forest sector, focusing on continuous cover forestry. This approach optimizes forest industry production, harvest levels, and logistic solutions based on market conditions. The method involves solving quadratic prog
0 views • 27 slides
Integrating Stochastic Weather Generator with Climate Change Projections for Water Resource Analysis
Exploring the use of a stochastic weather generator combined with downscaled General Circulation Models for climate change analysis in the California Department of Water Resources. The presentation outlines the motivation, weather-regime based generator description, scenario generation, and a case s
0 views • 20 slides
Understanding Stochastic Differential Equations and Numerical Integration
Explore the concepts of Brownian motion, integration of stochastic differential equations, and derivations by Einstein and Langevin. Learn about the assumptions, forces, and numerical integration methods in the context of stochastic processes. Discover the key results and equations that characterize
0 views • 6 slides
Understanding Vector Calculus II Concepts with Examples by Prof. Somesh Kr. Malhotra
Explore advanced topics in vector calculus including gradient, divergence, curl, and theorems like the Divergence Theorem and Stokes' Theorem. Follow along with examples presented in Cartesian, spherical, and cylindrical coordinates to deepen your understanding of vector calculus concepts.
0 views • 29 slides
Introduction to Generalized Stochastic Petri Nets (GSPN) in Manufacturing Systems
Explore Generalized Stochastic Petri Nets (GSPN) to model manufacturing systems and evaluate steady-state performances. Learn about stochastic Petri nets, inhibitors, priorities, and their applications through examples. Delve into models of unreliable machines, productions systems with priorities, a
0 views • 44 slides
Exploring Stochastic Algorithms: Monte Carlo and Las Vegas Variations
Stochastic algorithms, including Monte Carlo and Las Vegas variations, leverage randomness to tackle complex tasks efficiently. While Monte Carlo algorithms prioritize speed with some margin of error, Las Vegas algorithms guarantee accuracy but with variable runtime. They play a vital role in primal
0 views • 13 slides
Optimal Early Drought Detection Using Stochastic Process
Explore an optimal stopping approach for early drought detection, focusing on setting trigger levels based on precipitation measures. The goal is to determine the best time to send humanitarian aid by maximizing expected rewards and minimizing expected costs through suitable gain/risk functions. Tas
0 views • 4 slides
Optimizing User Behavior in Viral Marketing Using Stochastic Control
Explore the world of viral marketing and user behavior optimization through stochastic optimal control in the realm of human-centered machine learning. Discover strategies to maximize user activity in social networks by steering behaviors and understanding endogenous and exogenous events. Dive into
0 views • 15 slides
Understanding Tradeoff between Sample and Space Complexity in Stochastic Streams
Explore the relationship between sample and space complexity in stochastic streams to estimate distribution properties and solve various problems. The research delves into the tradeoff between the number of samples required to solve a problem and the space needed for the algorithm, covering topics s
0 views • 23 slides
Efficient Training of Dense Linear Models on FPGA with Low-Precision Data
Training dense linear models on FPGA with low-precision data offers increased hardware efficiency while maintaining statistical efficiency. This approach leverages stochastic rounding and multivariate trade-offs to optimize performance in machine learning tasks, particularly using Stochastic Gradien
0 views • 26 slides
Introduction to Relational Calculus and Algebra in Database Management
Explore the fundamental concepts of relational calculus and algebra in the domain of database management. Understand the differences between declarative and imperative query languages and learn to retrieve information using practical examples and theoretical frameworks such as tuple relational calcu
0 views • 23 slides