Interpolation and Pulse Shaping in Real-Time Digital Signal Processing
Discrete-to-continuous conversion, interpolation, pulse shaping techniques, and data conversion in real-time digital signal processing are discussed in this content. Topics include types of pulse shapes, sampling, continuous signal approximation, interpolation methods, and data conversion processes
5 views • 14 slides
Laplace Interpolation for Sparse Data Restoration
Laplace Interpolation is a method used in CSE 5400 by Joy Moore for interpolating sparse data points. It involves concepts such as the mean value property, handling boundary conditions, and using the A-times method. The process replaces missing data points with a designated value and approximates in
3 views • 13 slides
Quasi-Experiments in Research
Quasi-experiments are research studies that resemble experiments but do not involve random assignment of participants to treatment groups. This approach is taken when random assignment is challenging or when ethical considerations come into play. Unlike true experiments, quasi-experiments can provid
2 views • 15 slides
Curve Fitting Techniques
Curve fitting involves approximating function values using regression and interpolation. Regression aims to find a curve that closely matches target function values, while interpolation approximates points on a function using nearby data. This chapter covers least squares regression for fitting a st
1 views • 48 slides
Nonexperimental and Quasi-experimental Studies
Nonexperimental and quasi-experimental studies resemble experiments but lack random assignment, making them valuable for group comparisons without establishing causation. This type of research design looks at differences between groups that already exist, focusing on group differences rather than ca
2 views • 35 slides
Interpolation Techniques in Computer Analysis & Visualization
Explore the concepts of interpolation and curve fitting in computer analysis and visualization. Learn about linear regression, polynomial regression, and multiple variable regression. Dive into linear interpolation techniques and see how to apply them in Python using numpy. Uncover the basics of fin
4 views • 44 slides
Quasi-Judicial Roles and Ethical Responsibilities in Decision-Making
Exploring the distinction between legislative and quasi-judicial roles in decision-making processes, this content delves into examples, principles, and ethical responsibilities. It emphasizes fairness, impartiality, and the importance of public trust in upholding ethical standards within quasi-judic
0 views • 34 slides
Interpolation in Numerical Methods
Interpolation is a fundamental mathematical operation used in numerical methods to find the value of a function between known data points. It involves computing the value of a function at any point within a given interval based on existing data. Newton's forward interpolation formula is commonly use
1 views • 18 slides
Curl-Free and Div-Free Radial Basis Functions in Physical Situations
This content explores the applications of Curl-Free and Div-Free Radial Basis Functions in solving partial differential equations for fields, the theoretical soundness of using RBFs, and examples illustrating divergence-free interpolation. It also delves into matrix-valued RBF formulations, converge
4 views • 13 slides
Interpolation Techniques for Synthetic Aperture Radar (SAR) Implementation
Dive into the world of Synthetic Aperture Radar (SAR) implementation tools and techniques, including resampling methods, interpolation of band-limited signals, and the analysis of SAR-specific algorithms like range Doppler and chirp scaling. Explore how resampling algorithms enable non-uniform sampl
0 views • 35 slides
Enhancing Precipitation Interpolation Methods for High-Resolution Data Analysis
Accurate interpolation of precipitation data is crucial for various applications, especially in regions with limited data coverage like Greece. This study focuses on improving the creation of a precipitation atlas for Greece using daily observation analysis. By analyzing the reliability of the metho
0 views • 24 slides
Interpolation Methods in Physics
Interpolation in physics involves constructing a function that fits known data points to estimate values at arbitrary points. It is a method to fill in data gaps and is a specific case of curve fitting. Linear interpolation and polynomial interpolation are common methods used in this process, each w
1 views • 18 slides
Quasi-Interpolation for Scattered Data in High Dimensions: Methods and Applications
This research explores the use of quasi-interpolation techniques to approximate functions from scattered data points in high dimensions. It discusses the interpretation of Moving Least Squares (MLS) for direct pointwise approximation of differential operators, handling singularities, and improving a
1 views • 9 slides
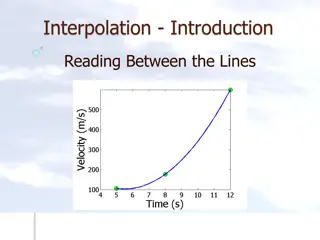
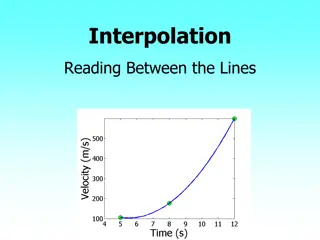
Interpolation: Reading Data Patterns & Solving Practical Problems
Explore the concept of interpolation through real-world examples like predicting values between data points and solving problems like rocket velocity calculation and heat transfer. Dive into understanding specific heat of carbon, thermistor calibration, and spline method of interpolation. Learn to f
0 views • 45 slides
Interpolation: Methods and Applications
Interpolation is a technique used to estimate values between known data points. This content covers the concept of interpolation, its applications in solving real-world problems like rocket velocity and specific heat calculations, and methods such as spline interpolation. Explore how interpolation h
1 views • 42 slides
Fast and Efficient MPM Solver for Strain Localization Problems
This study presents a fast and efficient Material Point Method (MPM) solver for strain localization problems, introducing the Generalized Interpolation Material Point Method (GIMPM) and Convected Particle Domain Interpolation (CPDI). The MPM computational phase involves mapping, nodal solution, and
0 views • 19 slides
Brief Overview of Interpolation Search and Algorithms
Explore Interpolation Search, variable decrease algorithms, and the efficiency of Insertion Sort. Understand the concept of decreasing by constant amount, factor or variable, and discover how interpolation search estimates the location of a key in a sorted array. Dive into the running time analysis
0 views • 30 slides
MATH 2140 Numerical Methods
Interpolation using a single polynomial in numerical methods gives insights into constructing a function passing through a set of data points. Various polynomial orders are utilized to connect data points efficiently, showcasing the importance of polynomial interpolation and extrapolation in mathema
0 views • 19 slides
Analyzing Interpolation and Extrapolation Techniques
Explore polynomial interpolation, Vandermonde matrix equations, condition numbers, proofs, norms, vector and matrix norms, and commonly used norms in mathematics. Understand the concepts and applications of interpolation and extrapolation through detailed explanations and visual aids.
0 views • 28 slides
Secret sharing using Lagrange interpolation polynomial
Learn about secret sharing using Lagrange interpolation polynomial in the context of innovative teaching and education in mathematics. Discover how this concept is applied and explore its significance in mathematical education. Visit the mentioned website for more information.
0 views • 14 slides
Theory of Approximation: Interpolation
In the study of approximation theory, interpolation plays a crucial role in representing data points using polynomials and splines. This content discusses the concepts of interpolation polynomials, including Newton's Divided Difference and Lagrange Polynomials, as well as spline interpolation techni
0 views • 16 slides
DFT and DTFT Interpolation
Delve into the relationship between Discrete Fourier Transform (DFT) and Discrete-Time Fourier Transform (DTFT) through interpolation. Explore how to derive DTFT from DFT samples, the synthesis and analysis formulas, the importance of sequence length in relation to N-point DFT, sampling strategies,
0 views • 13 slides
Applied Geostatistics Course Overview
This course introduces basic concepts and applications of applied geostatistics, focusing on spatial interpolation methods commonly used in various disciplines like geology, engineering, and geography. Students with a background in statistics or GIS can enhance their skills through hands-on learning
0 views • 29 slides
CSS3 Animations and Interpolation Overview
Delve into the world of CSS3 animations and interpolation techniques for creating dynamic and visually engaging web content. Learn about key frames, easing functions, types of animations, and how to seamlessly transition between values to enhance user experience.
0 views • 26 slides
Understanding Quasi-Definitive Data in Geomagnetic Research
Learn about Quasi-Definitive Data in geomagnetic research for 2015, including its importance, characteristics, and comparison with definitive data. Explore the concept of rapid data delivery and its relevance to scientific activities, particularly in the context of the Swarm satellite mission. Disco
0 views • 17 slides
Quasi-Orthogonal STBC in IEEE 802.11aj: Enhanced Wireless Communication
Explore the implementation of Quasi-Orthogonal Space-Time Block Coding (STBC) in IEEE 802.11aj for enhanced wireless communication. This research delves into coding schemes beyond traditional Alamouti codes, aiming to achieve improved performance in systems with multiple antennas. Discover how Quasi
0 views • 16 slides
Printed Quasi-Landstorfer Antenna by Masud Al Aziz
Explore the innovative design of a new printed quasi-Landstorfer antenna created by Masud Al Aziz. Learn about the evolution from traditional Yagi-Uda antennas to Quasi-Yagi and Landstorfer antennas, and how this new design aims to achieve high gain in a planar form factor. Discover the principles b
0 views • 23 slides
Kronecker Products-based Regularized Image Interpolation Techniques
Enhance your understanding of image interpolation with the Kronecker products-based regularized technique, presenting a parallel implementation for high-resolution image restoration from low-resolution noisy images. Explore the problem formulation, implementation model, and performance results of th
1 views • 4 slides
Quasi Random Sequences Fields of Use and Applications
Explore the diverse applications of quasi-random sequences in mathematics, computer science, physics, and finance. From solving differential equations to simulating ion transport, this comprehensive overview covers a wide range of fields where quasi-random sequences play a crucial role.
0 views • 5 slides
Understanding Spatial Interpolation and Extrapolation Techniques
Learn about the importance of spatial interpolation and extrapolation in estimating values between known points and beyond, along with popular methods like Thiessen Polygons and IDW.
1 views • 41 slides
Computational Geometry: Point Set Triangulation and Interpolation
Delve into the intricacies of point set triangulation and interpolation in computational geometry with topics covering height interpolation, triangulation complexity, and legal triangulation. Explore the existence and importance of triangulation in approximating terrains and learn about different in
0 views • 17 slides
Estimating Polynomial Regression with Lagrange Interpolation
Learn how to utilize Lagrange interpolation polynomial to estimate polynomial regression by creating quadratic Lagrange polynomials and producing the best prediction for data. Explore the challenges faced and results obtained, along with insights on why the sum of squares of error is a superior metr
0 views • 10 slides
Enhancing Speech-to-Text Generation with Interpolation Augmentation
Explore how Interpolation Augmentation (IPA) improves Speech-to-Text systems in low-resource scenarios by creating virtual samples through linear interpolation. This study combines IPA with existing data augmentation techniques for optimal results in speech recognition tasks.
0 views • 45 slides
Patchwise and Local Interpolation Techniques Explained
Discover the difference between patchwise and local interpolation techniques, understand the general procedure, special considerations, and various methods used in local interpolation. Explore interpolation within TIN and the assumptions behind linear interpolation methods.
1 views • 28 slides
Understanding Divided Differences in Polynomial Interpolation
Learn about divided differences, polynomial interpolation, and the unique nth-order polynomial that fits n+1 data points. Explore Divided-Difference Notation and how to compute first and second divided differences in various examples.
0 views • 23 slides
Understanding Spline Interpolation for Polynomial Approximation
Learn about spline interpolation for polynomial approximation, including linear and cubic splines. Understand how to construct cubic splines passing through given points using MATLAB. Discover the advantages of piecewise-polynomial approximation over single polynomial approximation in function appro
0 views • 23 slides
Spline Interpolation Methods Explained
Learn about spline interpolation methods including linear, quadratic, and cubic splines, their continuity requirements, and how to fit independent polynomials in each interval for accurate data approximation.
0 views • 16 slides
Understanding Interpolation and Numerical Methods in Mathematics
Explore the concept of interpolation, a fundamental operation in mathematics for computing function values within given intervals. Learn about Newton's forward interpolation formula and its application in solving problems like finding steam pressure at specific temperatures.
0 views • 18 slides
Understanding Quadratic Interpolation Method in Optimization
Explore the efficiency of quadratic interpolation method in optimization, focusing on normalization, approximation, and refitting stages. Learn how to apply this method with an example and iterations.
0 views • 6 slides
Advanced Embedded Systems Lecture: Direct Digital Synthesis and Interpolation
Learn about direct digital synthesis, linear interpolation, and look-up tables in advanced embedded systems. Discover how interpolation can help in creating missing data efficiently.
0 views • 24 slides