Mathematicians
Explore the lives and contributions of renowned mathematicians like Pythagoras, Aristotle, Euclid, Al-Khwarizmi, Leonardo da Vinci, Galileo Galilei, De Lhopital, and Leonhard Euler. From ancient Greece to modern-day Switzerland, learn about their work in areas such as geometry, algebra, calculus, an
28 views • 10 slides
The Joy of Sets: Graphical Alternatives to Euler and Venn Diagrams
Graphical representations of set membership can be effectively portrayed using alternatives to traditional Euler and Venn diagrams. Learn about upset plots, indicating set membership graphically, and the use of Venn or Euler diagrams as solutions. Explore the historical context and challenges with V
4 views • 43 slides
Maxwell Equations in Thermodynamics
In thermodynamics, Maxwell equations are derived using Euler's reciprocity relation. They involve characteristic functions such as internal energy, free energy, enthalpy, and Gibbs free energy, along with parameters like temperature, entropy, pressure, and volume. These equations form the foundation
2 views • 15 slides
Thermodynamics and Fluid Mechanics Fundamentals for Efficiency
Explore key concepts in thermodynamics and fluid mechanics such as the equation of continuity, the first law of thermodynamics, the momentum equation, Euler's equation, and more. Learn about efficiency, internal energy, and the laws governing energy transfer in various systems. Delve into topics lik
3 views • 12 slides
Classical Mechanics at Neotech Institute of Applied Science and Research, Virod
Delve into the world of Classical Mechanics in B.Sc Semester-V at Neotech Institute of Applied Science and Research, located in Virod, Vadodara. Explore topics such as motion of rigid bodies, angular momentum, Euler's theorem, inertia tensor, and Euler's equations of motion through a comprehensive s
1 views • 27 slides
Introduction to Gamma Function and Equivalent Integral Forms
The Gamma function is a versatile mathematical function that generalizes the factorial function to non-integer and complex values. It has various integral definitions such as the Euler-integral form. The proof of the factorial property of the Gamma function is demonstrated through analytical continu
4 views • 20 slides
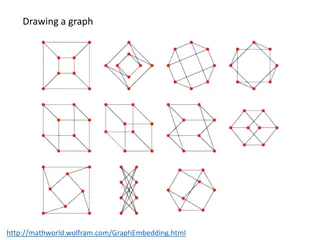
Graph Theory Fundamentals
Delve into the basics of graph theory with topics like graph embeddings, graph plotting, Kuratowski's theorem, planar graphs, Euler characteristic, trees, and more. Explore the principles behind graphs, their properties, and key theorems that define their structure and connectivity.
1 views • 17 slides
Dimensionless Velocity Triangles and Relations in Turbomachinery
Explore the concept of dimensionless velocity triangles for passive and active machines, power coefficients, Gibbs equation, static enthalpy coefficients, degree of reaction based on enthalpy and pressure changes, and Euler's turbine formula in kinematic form. Gain insights into the relationships an
2 views • 17 slides
Residue Systems and Euler's Phi Function in Mathematics
Residue Systems, also known as Reduced Residue Systems, play a significant role in number theory. They involve concepts like the Euler Phi Function, which counts integers relatively prime to a given number. Complete Residue Systems and their properties are explored, highlighting the least non-negati
8 views • 11 slides
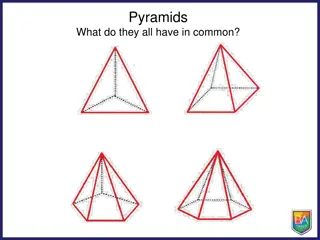
Pyramids and Prisms in Geometry
Explore the common characteristics of pyramids and prisms, learn about their definitions, faces, edges, and vertices, and understand Euler's formula for polyhedra. Discover the properties of different pyramids and prisms and predict results based on various base shapes. Verify Euler's formula for pr
1 views • 14 slides
Arithmetic Statistics in Function Fields
Delve into the world of arithmetic statistics in function fields, exploring concepts like the Divisor function, Dirichlet divisor problem, counting methods, Euler summation formula, and more. Discover the beauty of number theory through the lens of these mathematical functions and distributions.
0 views • 22 slides
Public Key Cryptosystems in RSA Encryption
Public key cryptosystems, like RSA, use two keys for encryption and decryption, with one key made public and the other kept secret. This asymmetric system allows secure communication, where the encryption key (E) is used to encrypt messages into ciphertext (C), which can only be decrypted back to th
2 views • 11 slides
Numerical Solution of Eulerian Advection Equation in 1-D Operator Splitting
Application of operator splitting over three directions allows reducing the Eulerian advection equation to 1-D, enabling finite differencing of derivatives while maintaining conservation properties. Various numerical schemes like forward Euler, leapfrog, and linear upstream are discussed, highlighti
3 views • 8 slides
Introduction to Dynamical Systems Math 319
Dive into the world of dynamical systems with a focus on applications like population growth, radioactive decay, and more. Learn about discrete time steps, multivariable models, and the essence of dynamical systems in tracking changes over time. Explore the simplicity of Euler's Method and the impor
2 views • 65 slides
Bounded Degree Polyhedronization of Point Sets in R3
The problem of finding a polyhedron in R3 with no four points coplanar, having the set of points as vertices, being simple in structure, with each vertex connected to O(1) edges, and featuring both a tetrahedralization and chain dual. This task has historical importance with Euler's formula setting
2 views • 24 slides
Randomness in Topology: Persistence Diagrams, Euler Characteristics, and Möbius Inversion
Exploring the concept of randomness in topology, this work delves into the fascinating realms of persistence diagrams, Euler characteristics, and Möbius inversion. Jointly presented with Amit Patel, the study uncovers the vast generalization of Möbius inversion as a principle of inclusion-exclusio
2 views • 57 slides
The Fascinating Euler Paths and the Seven Bridges of Konigsberg
Explore the intriguing world of Euler paths through the historical context of the Seven Bridges of Konigsberg. Learn about Leonhard Euler, the concept of Euler paths, and how to determine if a shape has a valid Euler path. Dive into the reasoning behind Euler paths and why they work with shapes of 0
3 views • 9 slides
Test
The Navier-Stokes equation and other fluid dynamics concepts are explored in this content. Topics covered include turbulent viscosity, Euler equation, continuity equation, turbulence behavior, Reynolds equations, and boundary conditions. The relationship between unknowns, properties of flow, and rel
0 views • 25 slides
Series in Mathematics
Explore the concept of series in math, including finite and infinite sequences, Euler's symbol for sum, and essential formulas for integers, squares, and cubes. Practice evaluating series sums and breaking up summations for deeper understanding.
1 views • 11 slides
Introduction to Graphs
Graph theory is a fundamental concept in computer science, allowing us to model and solve various problems. This lecture delves into the Seven Bridges of Konigsberg problem, exploring degrees, isomorphism, paths, cycles, connectedness, trees, and Eulerian cycles. By examining Euler's solution, we se
0 views • 67 slides
Trigonometry Tidbits
Discover Euler's formulas, equations, and insights on complex numbers in this in-depth workshop focused on enhancing trigonometry teaching. Uncover the beauty of mathematical identities and expand your understanding of complex numbers through engaging content and visual aids.
2 views • 21 slides
Practice Exam 3 CS 418 at University of Illinois at Urbana-Champaign
This content covers topics such as the de Casteljau Algorithm, Bezier properties, Half-Edge Data Structure, and Euler Integration in interactive computer graphics. It includes examples, explanations, and visuals to aid in understanding these concepts for CS 418 students at the University of Illinois
1 views • 11 slides
Graph Theory: Euler Paths and Circuits in Management Science
Euler Paths and Circuits in Graph Theory and Management Science, illustrated through the famous Konigsberg bridges problem and graph theory concepts. Understand vertices, edges, isomorphism, and graph modeling of relationships with examples like housing developments and student friendships.
2 views • 17 slides
Numerical Integration in Ordinary Differential Equations
Explore numerical methods for integrating ordinary differential equations (ODEs) with lecture notes covering one-step methods like Forward Euler, Backward Euler, and the Trapezoidal Rule. Understand how these methods are used to solve initial value problems (IVPs) when analytic solutions are not ava
2 views • 29 slides
Complex Numbers and Algebra: Understanding Phasors and Polar Forms
Dive into the world of complex numbers, phasors, and algebra in electromagnetic wave analysis. Learn about polar forms, Euler's identity, complex conjugates, addition, subtraction, multiplication, division, and square roots of complex numbers. Master the notation and mathematical operations essentia
2 views • 25 slides
Exploring Discrete Fourier Transform in Wireless Networks - LAB 1
Dive into the world of Discrete Fourier Transform with a focus on Wireless Networks LAB 1. Learn about complex signals, Euler's formula, DFT properties, and more through informative visual aids.
2 views • 14 slides
Complex Numbers: Cartesian vs Polar Form, Graphical Representation, Operations
Learn about complex numbers in Cartesian and polar forms, Euler's identity, graphical representation on a complex number plane, arithmetic operations, and conversion between forms. Explore examples and concepts related to complex numbers in the context of electric circuits and engineering.
0 views • 7 slides
Introduction to Newton's Equations for Fluids and Euler Analysis
This lecture delves into Newton's laws for fluids, exploring topics like the continuity equation, irrotational and incompressible fluids, and velocity potential derived from zero velocity curl. The class discusses the physical insights behind variables like epsilon, examines the significance of the
2 views • 29 slides
Newtonian Fluid Dynamics: Euler Formulation and Analysis
Dive into the principles of Newtonian fluid dynamics with a focus on Euler's formulation and analysis, encompassing Newton's equations for fluids, continuity equation, irrotational and incompressible fluids, and more. Explore the physical relationships, origins, and applications of key concepts in h
3 views • 36 slides
Rotations in Game Graphics: Quaternions, Matrices, and Euler Angles
Explore the concepts of rotation in game graphics through quaternions, rotation matrices, and Euler angles. Learn about representing rotation, interpolation, and complex transformations using quaternions and matrices for efficient game development.
3 views • 18 slides
Graph Theory in Management Science
Explore the concept of Euler paths and circuits in graph theory within the context of management science. Learn how graphs simplify complex problems, as demonstrated by Euler's analysis of the bridges in Konigsberg. Discover the language of graphs, including vertices and edges, and how they are used
3 views • 17 slides
Exploring NP-Completeness and Euler Circuits in Graph Theory
Discover the fascinating world of NP-Completeness, Euler Circuits, and graph theory with historical puzzles like the Seven Bridges of Königsberg. Learn about finding Euler circuits in connected, undirected graphs and the conditions for Euler tour existence. Dive into practical applications like ins
0 views • 51 slides
Graph Theory: Euler Paths & Cycles Overview
Delve into the world of graph theory with a focus on Euler paths and cycles. Explore the fundamentals, solve exercises, and learn about Euler's solution from 1736.
0 views • 20 slides
Euler's Method for Approximating Functions
Learn how to use Euler's method for approximating functions when direct solutions to differential equations are not possible. Discover the numerical techniques and steps involved in estimating values of functions at specific points. Explore the concept of tangent lines and their role in the approxim
3 views • 14 slides
Euler's Method for Numerical Solution to Differential Equations
Learn how Euler's method utilizes local linearity to approximate solutions to differential equations iteratively. Explore the step-by-step process and implications of choosing step sizes for accuracy. Discover how this method helps build solutions graphically with examples.
3 views • 11 slides
Numerical Methods for ODE Solving Techniques
Explore numerical methods like Euler's method and Runge-Kutta methods for solving ordinary differential equations. Understand step methods and basis of solutions to predict successive values of a function. Learn to integrate numerically using Euler's method and discover different variations like Heu
2 views • 21 slides
Understanding Euler's Method and Logistic Growth in Calculus
Learn about Euler's Method, a recursive process used in calculus to approximate solutions to differential equations, and explore Logistic Growth models for population dynamics. Discover how these concepts are applied in real-world scenarios and improve your understanding of advanced calculus topics.
3 views • 6 slides
Understanding Runge-Kutta Methods for Numerical Integration
Explore various Runge-Kutta methods including Euler, Modified Euler, Midpoint, Heun's, and RK4. Learn how these methods are applied to solve initial value problems and see computational examples for a better understanding of numerical integration techniques.
0 views • 34 slides
Enhanced Accuracy with Modified Euler Method
Learn how the Modified Euler method improves accuracy over the Euler method by incorporating estimation correction. Explore worked examples and understand the process step by step to find solutions accurately and efficiently.
0 views • 7 slides
Computational Methods in Engineering: ODE Solutions
Explore ordinary differential equations (ODE) and computational methods in engineering with a focus on multi-step, BDF, and Runge-Kutta techniques. Learn about initial value problems, explicit and implicit methods, as well as applications to systems of ODEs. The content covers multi-step methods suc
1 views • 24 slides