Euler's Method for Approximating Functions
Learn how to use Euler's method for approximating functions when direct solutions to differential equations are not possible. Discover the numerical techniques and steps involved in estimating values of functions at specific points. Explore the concept of tangent lines and their role in the approximation process.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
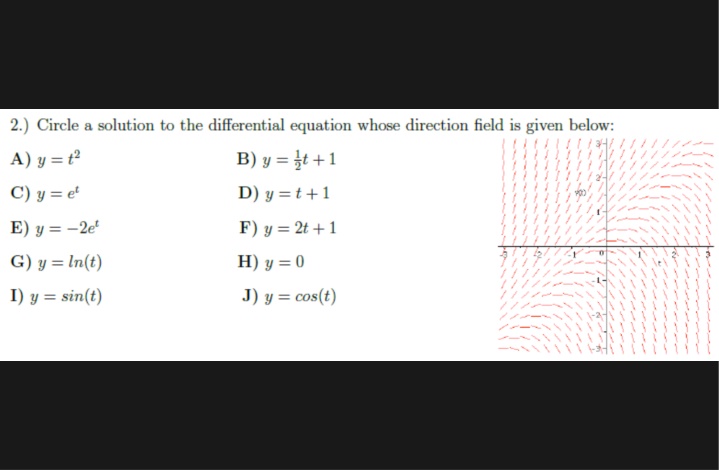
Section 2.7 Eulers method: Using tangent lines to approximate a function. We often cannot solve differential equations directly and thus need to use numerical methods to approximate solutions. For more info (and to earn a math minor), take MATH:3800 Introduction to Numerical Methods. Math minor info (15 math units): https://math.uiowa.edu/undergraduate- program/majors-minor/minor-requirements Or double major: eg Math Program C: Engineering https://math.uiowa.edu/sites/math.uiowa.edu/files/p rint_pdf/Engineering%20Program%20C%20Template% 202016%20.pdf http://slopefield.nathangrigg.net
?? + 1 = ?? + ? = ??+ ? ??,?? ? Part of tangent line at (??,??) Thus slope is ?(??,??) (??+ 1,??+ 1) Its length is determined by ? ? (??,??) ? = 0.1 (t2, y2) (t1, y1) (t3, y3) (t0, y0)
Estimate y(0.3) using h = Step size = t = 0.1 Thus if (?0,?0) = (0,0) the initial value, then (?? + 1,??+ 1) ?1 = 0.1 and ?1 = ?0 + ? = ?0+ ? ?0,?0 0.1 ? Slope at (?0,?0) ? (??,??) ? = 0.1 ?2 = 0.2 and ?2 = ?1 + ? = ?1+ ? ?1,?1 ?3 = 0.3 and ?3 = ?2 + ? = ?2+ ? ?2,?2 (0.1) (0.1)
h = Step size = t = 0.1
For the initial value problem, y = t2y, y(5) = 3, use Euler s method to estimate y(5.2) using t = 0.1
h = Step size = t = 0.1 Sequence of functions One function consisting of pasting together tangent lines
2.7: Glue together tangent lines to find a single function approximating y(t) h = Step size = t = 0.1 2.8: Find a sequence of functions that converge to y(t)
