Discrete Math for Computer Science Course - ICS 6D, Spring 2016
Prof. Sandy Irani leads the ICS 6D Discrete Math for Computer Science course at UC Irvine. The course covers various topics in discrete mathematics, with lectures on Mondays, Wednesdays, and Fridays. Teaching assistants and readers support the course, which includes interactive activities on zyBook.
5 views • 32 slides
Discrete Mathematics
Explore the foundations of logic and proofs in discrete mathematics, focusing on compound propositions, bit operations, and applications of propositional logic. Learn about how computers use bits for information representation and manipulation, and delve into translating English sentences into logic
5 views • 15 slides
Exploring Brain Waves Through EEG Analysis
Delve into the world of brain waves with EEG, EKG, and EMG measurements. Learn how to analyze brain wave data using mathematical processes like Fast Fourier Transform (FFT) and Power Spectral Density (PSD). Discover the significance of different frequencies in brain wave signals and how they reflect
1 views • 13 slides
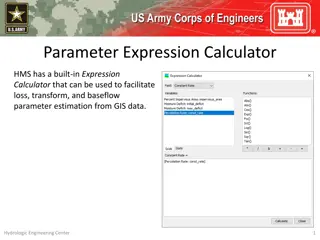
Parameter Expression Calculator for Efficient Parameter Estimation from GIS Data
Parameter Expression Calculator within HEC-HMS offers a convenient tool to estimate loss, transform, and baseflow parameters using GIS data. It includes various options such as Deficit and Constant Loss, Green and Ampt Transform, Mod Clark Transform, Clark Transform, S-Graph, and Linear Reservoir. U
1 views • 5 slides
Understanding Divisibility and Modular Arithmetic in Discrete Structures
This lecture discusses the concepts of divisibility and modular arithmetic in the context of discrete structures. It covers definitions, notation, and examples of divisibility by integers, including proving properties such as the divisibility of products and consecutive integers. Through practical e
1 views • 43 slides
Advancements in Discrete Auto Analyzers for Clinical Chemistry Operations
Discrete auto analyzers integrate specimen handling, reagent systems, optical components, and computers for streamlined functionality. The innovation in computer technology, particularly microprocessors, has revolutionized these analyzers, enabling precise data management, liquid handling, and optic
0 views • 17 slides
Exploring GPU Parallelization for 2D Convolution Optimization
Our project focuses on enhancing the efficiency of 2D convolutions by implementing parallelization with GPUs. We delve into the significance of convolutions, strategies for parallelization, challenges faced, and the outcomes achieved. Through comparing direct convolution to Fast Fourier Transform (F
0 views • 29 slides
Microeconometric Modeling with Multinomial Logit Model
The topic discusses the Multinomial Logit Model in the context of discrete choice modeling, covering concepts, models, consumer preferences, utility maximization, and implications for discrete choice models. It explores how consumers maximize utility under budget constraints, the need for well-defin
1 views • 58 slides
Understanding Fourier Analysis and Its Applications
Fourier analysis is essential in representing periodic functions using Fourier series, allowing for solving differential equations and approximating complex functions. The method extends to nonperiodic phenomena through Fourier integrals and transforms, with significant applications in engineering a
0 views • 21 slides
Understanding Discrete Optimization in Mathematical Modeling
Discrete Optimization is a field of applied mathematics that uses techniques from combinatorics, graph theory, linear programming, and algorithms to solve optimization problems over discrete structures. This involves creating mathematical models, defining objective functions, decision variables, and
0 views • 12 slides
Understanding Sampling and Signal Processing Fundamentals
Sampling plays a crucial role in converting continuous-time signals into discrete-time signals for processing. This lecture covers periodic sampling, ideal sampling, Fourier transforms, Nyquist-Shannon sampling, and the processing of band-limited signals. It delves into the relationship between peri
1 views • 60 slides
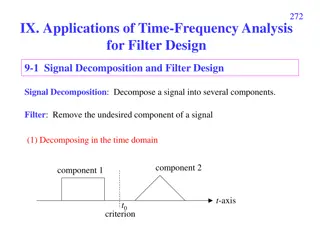
Applications of Time-Frequency Analysis for Filter Design
Signal decomposition and filter design techniques are explored using time-frequency analysis. Signals can be decomposed in both time and frequency domains to extract desired components or remove noise. Various transform methods like the Fourier transform and fractional Fourier transform are employed
1 views • 35 slides
Understanding Fourier Transforms and Properties
Fourier transforms play a crucial role in signal processing by transforming signals between time and frequency domains. This outline covers the basics of Fourier transforms, discrete Fourier transforms, Fourier series, properties like symmetry and reciprocity, resolution in time and frequency, the D
0 views • 5 slides
Introduction to Data Analysis in Geophysics with Seismic Analysis Code - SAC Lab 2.1
Explore the world of geophysics data analysis using the SAC Lab 2.1 code. Learn about seismic analysis, Fourier transform analysis, spectral analysis, color tracing, integration, differentiation, and more. The SAC online documentation provides valuable resources for users to delve deeper into this f
0 views • 45 slides
Carnegie Mellon Algebraic Signal Processing Theory Overview
Carnegie Mellon University is at the forefront of Algebraic Signal Processing Theory, focusing on linear signal processing in the discrete domain. Their research covers concepts such as z-transform, C-transform, Fourier transform, and various signal models and filters. The key concept lies in the al
2 views • 40 slides
Understanding Discrete Probability Distributions
Explore the definition of random variables, probability distributions, and three types of discrete distributions - Binomial, Hypergeometric, and Poisson. Learn about the mean, variance, and standard deviation of probability distributions, as well as the difference between discrete and continuous dis
3 views • 32 slides
Exploring Discrete Mathematics through Graph Theory
Delve into the world of discrete mathematics with a focus on graph theory. Learn about graphs, their properties, and essential theorems. Discover how graphs model relations in various applications like network routing, GPS guidance, and chemical reaction simulations. Explore graph terminology, theor
0 views • 26 slides
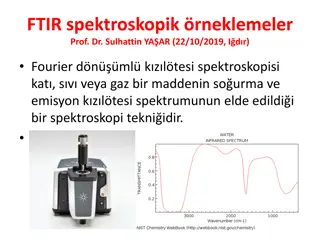
Fourier Transform Infrared (FTIR) Spectroscopy Examples by Prof. Dr. Sulhattin YAŞAR
Fourier Transform Infrared (FTIR) spectroscopy is a technique used to obtain the absorption and emission spectra of solid, liquid, or gas substances. This content provides characteristic absorption peaks for various functional groups, such as alkane, alkyl, alkenyl, alkynyl, aromatic compounds, alco
0 views • 15 slides
Cosmic Shear Measurement in Fourier Space and Its Scientific Goals
Exploring the cosmic shear in Fourier space with a collaborative effort led by Jun Zhang from Shanghai Jiao Tong University sheds light on fundamental scientific questions related to dark energy, the geometry of the universe, General Relativity, cold dark matter, and cosmic structure density distrib
0 views • 48 slides
Optical Security with Double Random Fractional Fourier Domain Encoding
Utilizing double random fractional Fourier domain encoding for optical security involves encryption and decryption methods based on the fractional Fourier transform of various orders, involving specific mathematical operations and notations. The process includes transforming the input function, encr
0 views • 13 slides
Understanding Combinatorics in Discrete Mathematics
Combinatorics, a key facet of discrete mathematics, explores the arrangement of objects and finds applications in various fields like discrete probability and algorithm analysis. The Rule of Sum, a fundamental principle, dictates how tasks can be accomplished when they cannot be done simultaneously.
0 views • 70 slides
Understanding Laplace Transforms for Continuous Random Variables
The Laplace transform is introduced as a generating function for common continuous random variables, complementing the z-transform for discrete ones. By using the Laplace transform, complex evaluations become simplified, making it easy to analyze different types of transforms. The transform of a con
0 views • 17 slides
Generating Random Variables Using Inverse Transform Method
Explore the Inverse Transform Method for generating random variables in simulations. Learn how to map random instances to desired distributions, whether continuous or discrete, by understanding cumulative distribution functions and inverting them. Examples and step-by-step explanations provided for
0 views • 24 slides
Understanding Errors in Radio Astronomy Imaging
Errors in radio astronomy imaging can occur in the uv plane and image plane due to various factors such as measurement errors, calibration imperfections, and approximations made during processing. Different error types like additive, multiplicative, and convolutional errors impact the quality of ast
1 views • 40 slides
Understanding GPU-Accelerated Fast Fourier Transform
Today's lecture delves into the realm of GPU-accelerated Fast Fourier Transform (cuFFT), exploring the frequency content present in signals, Discrete Fourier Transform (DFT) formulations, roots of unity, and an alternative approach for DFT calculation. The lecture showcases the efficiency of GPU-bas
0 views • 40 slides
Introduction to Sequential Pattern Mining Overview
Discover the concept of sequential pattern mining, a popular data mining task introduced in 1994, with a focus on analyzing discrete sequences to find interesting patterns. Sequential pattern mining involves finding frequent subsequences in sets of discrete sequences, such as items purchased by cust
1 views • 24 slides
Understanding Valid and Invalid Arguments in Discrete Mathematics
Concepts of valid and invalid arguments in discrete mathematics are explored through examples. Learn how to determine the validity of arguments based on premises and conclusions. Practice using truth tables to evaluate argument forms. Enhance your logical reasoning skills in Discrete Mathematics.
0 views • 22 slides
Understanding Yukawa Textures and Spectral Data in Computing
Exploring the low energy limit of the Heterotic string, focusing on Yukawa couplings and spectral data in the context of Calabi-Yau threefold and Weierstrass elliptically fibered CY3. The goal involves direct computation of challenging cohomologies and utilizing Fourier-Mukai transform for bundle co
0 views • 17 slides
Discrete Scenarios in Graphs
The scenarios where the height of a student depending on age, time taken in a race depending on distance, number of students taking a test depending on class size, and length of a walkway depending on number of bricks are analyzed to determine which would result in a discrete graph with isolated poi
1 views • 23 slides
Understanding Discrete Random Variables and Variance Relationships
Explore the concepts of independence in random variables, shifting variances, and facts about variance in the context of discrete random variables. Learn about key relationships such as Var(X + Y) = Var(X) + Var(Y) and discover common patterns in the Discrete Random Variable Zoo. Embrace the goal of
0 views • 27 slides
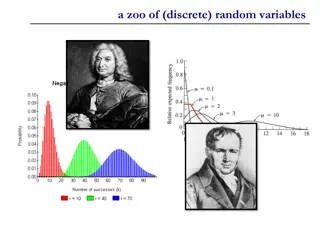
Understanding a Zoo of Discrete Random Variables
Discrete random variables play a crucial role in probability theory and statistics. This content explores three key types: Bernoulli random variable, binomial random variable, and error-correcting codes. From understanding the basics of Bernoulli trials to exploring the application of error correcti
0 views • 27 slides
Discrete Optimization Methods Overview
Discrete optimization methods, such as total enumeration and constraint relaxations, are valuable techniques for solving problems with discrete decision variables. Total enumeration involves exhaustively trying all possibilities to find optimal solutions, while constraint relaxations offer a more tr
0 views • 80 slides
Predicates and Quantifiers Exercise Solutions in Discrete Mathematics
Exercise solutions involving predicates and quantifiers related to printer status, job status, and queueing in a discrete mathematical context. The solutions address scenarios like lost jobs, busy printers, queued jobs, and out-of-service printers. References to textbooks in discrete mathematics are
0 views • 4 slides
Understanding Fourier Theory in Seismic Processing
Fourier theory plays a crucial role in seismic processing by helping to avoid temporal and spatial aliasing. It emphasizes the importance of sampling rates for accurate waveform reconstruction and highlights the significance of oversampling to prevent aliasing issues. Spatial aliasing is discussed i
0 views • 18 slides
Comprehensive Overview of Mathematical Methods and Resources
Covering topics such as interpolation, curve fitting, algebraic equations, transcendental equations, numerical differentiation, integration, Fourier series, Fourier transforms, partial differential equations, vector calculus, and finite difference methods. Includes recommended textbooks and referenc
0 views • 150 slides
Understanding Differential Equations and Boundary Value Problems
Explore the world of Differential Equations (DE) with a focus on Boundary Value Problems, guided by Dennis G. Zill and Michael R. Cullen. Dive into the realm of First Order and Higher Order DE, Partial DE, Laplace Transform, Fourier Series, and more. Unravel the complexities of DE through various se
0 views • 33 slides
Understanding Cyclic Groups and Discrete Logarithms
Exploring the concepts of cyclic groups and discrete logarithms in group theory. This presentation covers the definition of generators, examples of cyclic groups, important theorems related to prime orders and cyclic groups, uniform sampling in cyclic groups, and the discrete logarithm problem. Exam
0 views • 14 slides
Fourier-transform Infrared Spectroscopy Analysis of Jatropha curcas Latex Silver Nanoparticles
Utilizing Fourier-transform infrared spectroscopy, this paper discusses the analysis of hexane/methanol extracts of Jatropha curcas latex silver nanoparticles. The study explores the biosynthesis of nanoparticles using plant secondary metabolites as reducing agents, highlighting the medicinal proper
0 views • 15 slides
Cooley-Tukey Decimation in Time Algorithm
Explore the Cooley-Tukey decimation-in-time algorithm for computing the Discrete Fourier Transform efficiently. Understand how the algorithm splits the DFT computation into smaller parts and realize the benefits in terms of reduced number of multiplications. Dive into signal flowgraph notation for a
0 views • 12 slides
Understanding Fast Fourier Transform (FFT) in Signal Processing
Fast Fourier Transform (FFT) is a powerful algorithm used in signal processing to efficiently calculate the Discrete Fourier Transform (DFT). This advanced technique leverages symmetry and periodicity properties to reduce computational complexity, making it a key tool in digital signal analysis. By
0 views • 14 slides