Understanding Fast Fourier Transform (FFT) in Signal Processing
Fast Fourier Transform (FFT) is a powerful algorithm used in signal processing to efficiently calculate the Discrete Fourier Transform (DFT). This advanced technique leverages symmetry and periodicity properties to reduce computational complexity, making it a key tool in digital signal analysis. By decomposing a signal into frequency components, FFT enables a faster computation of spectral information, vital for various applications such as audio processing, image analysis, and telecommunications.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
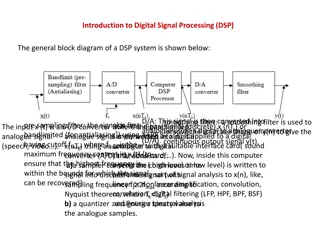
Discrete Fourier Transform The DFT pair was given as 1 N 1 k N 1 = k ( ) k j 2 / N kn x [ n ] = X e = n ( ) j 2 / N kn X = x [ n ] e Baseline for computational complexity: Each DFT coefficient requires N complex multiplications N-1 complex additions All N DFT coefficients require N2 complex multiplications N(N-1) complex additions Complexity in terms of real operations 4N2 real multiplications 2N(N-1) real additions Most fast methods are based on symmetry properties Conjugate symmetry Periodicity in n and k N 0 0 ( ) ( k ) ( ) ( ) ( k ) ( )kn j 2 / N N n j 2 / N kN j 2 / N n j 2 / N e e = e ( 2 e = N e ( ) ) ( k ) ( )( )n j 2 / N kn j / N n + N j 2 / N k + = e = e 2
FFT 6
Decimation-In-Time FFT Algorithms Makes use of both symmetry and periodicity Consider special case of N an integer power of 2 Separate x[n] into two sequence of length N/2 Even indexed samples in the first sequence Odd indexed samples in the other sequence N 1 N 1 N 1 k Substitute variables n=2r for n even and n=2r+1 for odd = 0 n even n odd n ( ) ( ) ( ) j 2 / N kn j 2 / N kn j 2 / N kn X = x [ n ] e = x [ n ] e + x [ n ] e N / = 2 1 N / = 2 1 k ( ) 2 N rk 2 r + 1 k X = ] r 2 [ x W + x [ 2 r + W ] 1 N r 0 r 0 N / = 2 1 N / = 2 1 G[k] and H[k] are the N/2-point DFT s of each subsequence W ] r 2 [ x 0 r + = rk N k N rk N = + W x [ 2 r + W ] 1 / 2 / 2 r 0 k k k N G W H 7
Decimation In Time 8-point DFT example using decimation-in-time Two N/2-point DFTs 2(N/2)2 complex multiplications 2(N/2)2 complex additions Combining the DFT outputs N complex multiplications N complex additions Total complexity N2/2+N complex multiplications N2/2+N complex additions More efficient than direct DFT Repeat same process Divide N/2-point DFTs into Two N/4-point DFTs Combine outputs 8
Decimation In Time Contd After two steps of decimation in time Repeat until we re left with two-point DFT s 9
Decimation-In-Time FFT Algorithm Final flow graph for 8-point decimation in time Complexity: Nlog2N complex multiplications and additions 10
Butterfly Computation Flow graph constitutes of butterflies We can implement each butterfly with one multiplication Final complexity for decimation-in-time FFT (N/2)log2N complex multiplications and additions 11
In-Place Computation Decimation-in-time flow graphs require two sets of registers Input and output for each stage Note the arrangement of the input indices Bit reversed indexing 7 7 x 111 x X 0 = x 0 X 000 = x 000 0 0 X 1 = x 4 X 001 = x 100 0 0 X 2 = x 2 X 010 = x 010 0 0 X 3 = x 6 X 011 = x 110 0 0 X 4 = x 1 X 100 = x 001 0 0 X 5 = x 5 X 101 = x 101 0 0 X 6 = x 3 X 110 = x 011 0 0 X = X 111 = 0 0 12
Decimation-In-Frequency FFT Algorithm The DFT equation N 1 nk N X k = W ] n [ x n = 0 Split the DFT equation into even and odd frequency indexes = n 0 n N / 2 1 x N 1 N 1 = N n N 2 r n N 2 r n N 2 r X 2 r = W ] n [ x = W ] n [ + W ] n [ x = 0 n / 2 Substitute variables to get = 0 n N / 2 1 x N / 2 1 x N / 2 1 ( ) = n = n ( ) n N 2 r n + N / 2 2 r nr N X 2 r = W ] n [ + [ n + N / W ] 2 = x [ n ] + x [ n + N / 2 ] W N / 2 0 0 Similarly for odd-numbered frequencies + 1 r 2 X N / 2 1 ( ) = n ( / ) n N 2 r + 1 = x [ n ] x [ n + N / 2 ] W 2 0 13
Decimation-In-Frequency FFT Algorithm Final flow graph for 8-point decimation in frequency 14