Matrices in Precalculus: Order, Augmented Matrix, and Row-Echelon Form
Delve into the world of matrices in Precalculus with a focus on identifying matrix orders, creating augmented matrices for systems of equations, transforming matrices into row-echelon form, and solving linear equations using matrices. Explore elementary row operations, row-echelon form, and reduced
2 views • 37 slides
Generalized Discriminant Analysis (GDA) in Pattern Recognition
Generalized Discriminant Analysis (GDA) is a nonlinear form of Linear Discriminant Analysis (LDA) that utilizes kernel methods to find discriminatory features for optimal class separability. LDA aims to maximize the between-class covariance matrix while minimizing the within-class covariance matrix.
2 views • 17 slides
Multivariate Normal Distribution and Simulation in PROC SIMNORM
Explore the concepts of multivariate normal distribution, linear combinations, subsets, and variance-covariance in statistical analysis. Learn to simulate data using PROC SIMNORM and analyze variance-covariance from existing datasets to gain insights into multivariate distributions. Visualize data t
1 views • 16 slides
Singular Value Decomposition
The Singular Value Decomposition (SVD) is a powerful factorization method for matrices, extending the concept of eigenvectors and eigenvalues to non-symmetric matrices. This decomposition allows any matrix to be expressed as the product of three matrices: two orthogonal matrices and a diagonal matri
0 views • 35 slides
Introduction to Matrices in Mathematical Analysis
Matrices play a crucial role in simplifying complex systems of equations and are well-suited for systematic mathematical treatments and computer computations. This introduction covers the definition of matrices, their properties such as size and notation, and various types of matrices including colu
0 views • 77 slides
Matrices and Solving Equations in Electrical Engineering
Matrices play a crucial role in solving linear equations in Electrical Engineering applications. Learn about matrix structures, special matrices, inverses, transposes, system of linear equations, and solving methods using MATLAB/Python. Explore the application of matrices in solving voltage-current
3 views • 24 slides
Correlation and Covariance in Business Analytics
Explore the concepts of covariance and correlation in business analytics to understand the relationship between random variables. Delve into how these measures help analyze dependence between variables, differentiate between independence and covariance, and interpret correlation as a dimensionless m
4 views • 27 slides
Learning-Based Low-Rank Approximations and Linear Sketches
Exploring learning-based low-rank approximations and linear sketches in matrices, including techniques like dimensionality reduction, regression, and streaming algorithms. Discusses the use of random matrices, sparse matrices, and the concept of low-rank approximation through singular value decompos
0 views • 13 slides
Measures of Linear Relationship in Statistics
Exploring the concepts of covariance and correlation coefficient in statistics to determine the strength and direction of linear relationships between variables. Covariance indicates the pattern two variables move together, while correlation coefficient quantifies the strength of the relationship. S
0 views • 35 slides
MATLAB Basics for Electrical Engineering Students
In this instructional content from the Government Polytechnic West Champaran Department of Electrical Engineering, students are introduced to the fundamentals of MATLAB. Topics covered include transposing matrices, concatenating matrices, matrix generators, arrays, entering matrices, and manipulatin
0 views • 48 slides
Variance and Covariance in Probabilistic System Analysis
Variance and covariance play crucial roles in probabilistic system analysis. Variance measures the variability in a probability distribution, while covariance describes the relationship between two random variables. This lecture by Dr. Erwin Sitompul at President University delves into these concept
4 views • 30 slides
Investigation of Observation-Informed Generalized Hybrid Error Covariance Models
In the field of meteorology and oceanography, the study focuses on the development of hybrid error covariance models that combine flow-dependent and climatologically-based estimates for improved data assimilation. The research aims to determine optimal hybridization parameters through innovative met
0 views • 14 slides
Traits, Factories, BUMP and Binding in Model Interfacing
This article delves into the use of Traits and Factories in handling class implementations within models. It covers the specific roles of Traits such as Geometry, State, and Increment, along with Factories like Model, Bias, Error Covariance, Localization, and Change Variables. BUMP, a generic implem
0 views • 21 slides
Inverse of Elementary Matrices & RREF Comparison
Inverse of elementary matrices explained with matrices operations, including row interchange, scaling, and row addition. How to find elementary matrices depicted step-by-step. Relationship between reduced row echelon form (RREF) and elementary matrices. The concept of invertible matrices and their r
0 views • 8 slides
Joint Distribution Functions, Independence of Random Variables, Covariance, and Correlation
This lecture covers the concepts of joint distribution functions, independence of random variables, covariance, correlation, and standby redundancy analysis in the context of engineering applications. It explores the probability density functions and failure scenarios of components in a standby syst
0 views • 13 slides
Confirmatory Factor Analysis in R with lavaan
In this guide on Confirmatory Factor Analysis (CFA) using lavaan in R, you will learn the basics with a motivating example, model fit statistics, and practical implementation steps. Understand the variance-covariance matrix, path diagram, model-implied covariance matrix, and more. Explore one-factor
0 views • 54 slides
Data Analysis for Business: Lists, Matrices, and Dataframes
Learn about lists, matrices, and dataframes in data analysis for business. Explore how lists are versatile and can contain multiple data types. Discover how matrices are used to represent multidimensional data, with examples on indexing and building matrices. Understand the importance of dataframes
0 views • 12 slides
Determinants in Matrices
Concept of determinants in matrices, this chapter delves into the significance of determinants in reflecting matrix characteristics and facilitating matrix comparisons. Learn about the evaluation of determinants using elementary row operations, properties of determinants, and the application of dete
0 views • 53 slides
Recap on Correlation Strength and Covariance
This content provides a recap on correlation strength, highlighting the relationship between variables based on their correlation value. It also touches on covariance, explaining how variables vary with each other. The examples and explanations help in understanding these statistical concepts better
0 views • 27 slides
Portfolio theory
In the realm of finance, portfolio theory plays a crucial role in investment decisions by analyzing the relationship between assets and returns. Descriptive statistics, on the other hand, provide valuable insights from data regarding means, variances, and standard deviations. Covariance and correlat
0 views • 11 slides
Mathematics Fundamentals - Matrices and Determinants
Fundamentals of matrices and determinants, including types of matrices like square matrices, column matrices, identity matrices, zero matrices, and more. Learn about operations on matrices, such as addition, subtraction, multiplication by constants, and transpose. Discover how matrices are used in r
0 views • 10 slides
Exploring Matrix Sketching Techniques for Data Analysis
This study delves into the use of matrix sketching over sliding windows for analyzing modern data sets represented as large matrices. Techniques such as Singular Value Decomposition (SVD), Principal Component Analysis (PCA), and K-means clustering are explored in the context of covariance matrices a
1 views • 21 slides
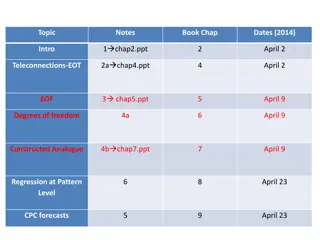
Understanding Empirical Orthogonal Functions (EOF) and Principal Component Analysis (PCA)
This text delves into the concept of Empirical Orthogonal Functions (EOF) and Principal Component Analysis (PCA) in meteorology, discussing methods, definitions, and the covariance matrix used in analyzing space-time relationships. It explains how EOFs help in reducing the dimensionality of data set
0 views • 37 slides
Variance and Covariance in Probabilistic System Analysis
Explore the concept of variance and covariance in probabilistic system analysis, understanding the importance of variability in probability distributions. Learn how to calculate variances for different scenarios and apply them to real-world examples to analyze data variability effectively.
0 views • 30 slides
Extensions of Linear Regression Model: Concepts and Applications
Explore the various extensions of the linear regression model in microeconometric modeling, covering topics such as quantile regression, robust covariance matrices, heteroscedasticity, and bootstrapping for estimating variances of estimators. Learn about robust inference, hypothesis testing, and con
0 views • 17 slides
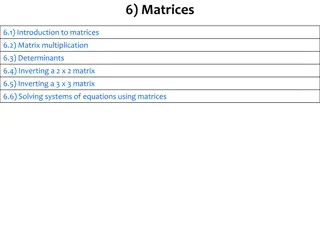
Understanding Matrices: Multiplication, Determinants, Inversion, & More
Explore the world of matrices with topics like matrix multiplication, determinants, inverting matrices, and solving systems of equations. Learn about matrix sizes, identity matrices, and how to find products. Dive into the realm of mathematics with practical examples and exercises.
0 views • 39 slides
Understanding Orthogonal Functions and Covariance in Geophysics
Explore the fundamentals of orthogonal functions and covariance, crucial in geophysical studies. Learn about basis functions, orthonormality, variance representation, and Fourier power spectrum. Gain insights into how orthogonal functions contribute to functional data representation and spectral ana
0 views • 21 slides
Understanding Multidimensional Gaussians and Covariance in Machine Learning
Explore the concept of multidimensional Gaussians in machine learning, from random vectors to covariance matrices. Learn about unequal variances and independence in two-dimensional data points with insightful visuals to deepen your understanding.
0 views • 25 slides
Agency Bayesian Optimization with Gaussian Processes
Explore the role of covariance functions in Gaussian processes for active machine learning and agency applications. Understand how kernel functions create covariance matrices, influencing the distribution of function values. Learn about smoothness assumptions, signal variance, noise variance, and mo
0 views • 49 slides
Matrix and Graph: Understanding Data Structures and Operations
Dive into the world of matrix and graph data structures, exploring their versatile applications from physical simulations to customer management. Learn about binary matrices, sparse matrices, adjacency matrices, and efficient operations for vectors and matrices. Discover how to represent complex dat
0 views • 44 slides
Estimation of Graphical Models Using Generalized Covariance Matrices
Explore the structure estimation for discrete graphical models by analyzing the relationships between conditional independence and inverse covariance matrices. The extension of Gaussian graphical models, Ising models, and more is discussed, providing insights into graph structures based on covarianc
0 views • 16 slides
Genetic Covariance Structure Analysis in Classical Twin Design
Explore the classical twin design and genetic covariance structure analysis, focusing on inferring genetic effects without measuring genes. Learn about genetically informative designs, covariance structures, multivariate models, and assumptions underlying the classical twin design. Discover how to f
0 views • 56 slides
Progress of IRSN on Nuclear Data Assessment for Molybdenum
Explore the progress made by IRSN on nuclear data assessment for Molybdenum through working package WP2 & 4. The assessment focuses on producing Mo evaluation with covariance for RP and cross sections using various sources like JEFF-33, ENDF/B-VIII.0, and JENDL-4.0. The project involves fitting expe
0 views • 7 slides
Verification and Testing of Covariance Libraries: Insights and Improvements
Explore the current verification and testing processes of covariance libraries, including automatic checks, corrections, and data inspections. Learn about the AMPX system, data uncertainty propagation, and suggestions for enhancements in validation and benchmark measurements. Find out what's missing
0 views • 8 slides
Discussing P-Matrices in IEEE 802.11-19/1910r0 for Enhanced High Throughput
This contribution explores the use of P-matrices with zero entries in IEEE 802.11-19/1910r0 to support more than 8 TX chains. It highlights the advantages of considering these matrices in Enhanced High Throughput (EHT) scenarios, showcasing their benefits for various MIMO configurations. The discuss
0 views • 13 slides
Understanding Matrices and Determinants in Algebra
Explore the concept of matrices and determinants in algebra through transformations, area calculations, and determinant properties. Learn about the significance of determinants, different transformations represented by matrices, and how to find determinants of various matrices. Dive into examples an
0 views • 10 slides
Understanding Determinants and Diagonalization of Square Matrices
Dive into the world of determinants and diagonalization of square matrices, learning how to find determinants, diagonalize matrices, and explore triangular matrices. Discover the properties and calculations involved, along with examples to enhance your understanding.
0 views • 32 slides
Understanding Matrices in Computer Science
Explore the world of matrices in computer science with topics covering square matrices, diagonal matrices, scalar matrices, identity matrices, zero matrices, and more. Learn about dimensions of matrices and practical examples to enhance your knowledge in this field.
0 views • 17 slides
Understanding Matrices: Types, Operations, and Properties
Explore the world of matrices - from defining what a matrix is to understanding different types like triangular, diagonal, and identity matrices. Learn about operations such as addition, subtraction, scalar multiplication, and matrix multiplication. Discover the significance of singular and non-sing
0 views • 22 slides
Discussing P Matrices for EHT in IEEE 802.11-19/1555r0 Document
This contribution explores the requirements, design options, and examples of P matrices for Enhanced High Throughput (EHT) in IEEE 802.11-19/1555r0. It covers the importance of P matrices for MIMO channel estimation, dimensions needed for EHT matrices, and the orthogonality aspect in EHT matrices to
0 views • 15 slides