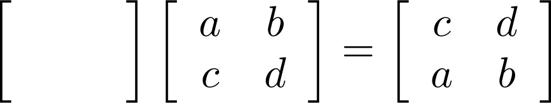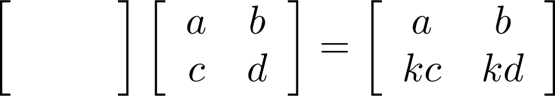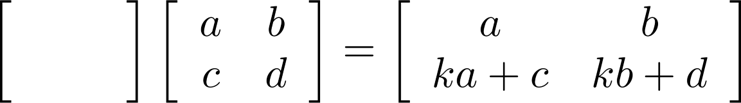Inverse of Elementary Matrices & RREF Comparison

Inverse of elementary matrices explained with matrices operations, including row interchange, scaling, and row addition. How to find elementary matrices depicted step-by-step. Relationship between reduced row echelon form (RREF) and elementary matrices. The concept of invertible matrices and their relationship with RREF. Highlighting the process of matrix inversion using elementary operations.

• Matrices
• Elementary Matrices
• Inverse
• RREF
• Matrix Operations

kell_len Follow

Uploaded on Feb 18, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Inverse of Elementary Matrices

2. Elementary Row Operation Every elementary row operation can be performed by matrix multiplication. 1. Interchange elementary matrix 1 0 1 0 2. Scaling 0 1 0 k 3. Adding k times row i to row j: 0 1 k 1

3. Elementary Matrix Every elementary row operation can be performed by matrix multiplication. How to find elementary matrix? elementary matrix E.g. the elementary matrix that exchanges the 1st and 2nd rows 1 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 1 2 3 4 5 6 2 1 3 5 4 6 ? ? = = 0 1 0 1 0 0 0 0 1 ? =

4. Elementary Matrix How to find elementary matrix? Apply the desired elementary row operation on Identity matrix 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 1 1 0 0 1 0 0 1 0 2 0 0 1 0 1 0 Exchange the 2nd and 3rd rows ?1= 0 0 0 1 Multiply the 2nd row by -4 ?2= 4 0 0 1 0 0 0 1 Adding 2 times row 1 to row 3 ?3=

5. Elementary Matrix How to find elementary matrix? Apply the desired elementary row operation on Identity matrix 1 0 0 1 0 0 1 0 2 0 0 1 0 1 0 1 2 3 4 5 6 1 3 2 4 6 5 ?1= ? = ?1? = 0 0 0 1 1 4 ?2= 4 0 0 1 0 ?2? = 8 3 1 2 5 20 6 4 5 14 0 0 1 ?3= ?3? =

6. Inverse of Elementary Matrix Reverse elementary row operation Exchange the 2nd and 3rd rows Exchange the 2nd and 3rd rows 1 0 0 1 0 0 0 0 1 0 1 0 0 0 1 0 1 0 1= ?1= ?1 Multiply the 2nd row by -4 Multiply the 2nd row by -1/4 1 0 0 1 0 0 0 0 0 1 0 0 0 1 1= ?2= 4 0 ?2 1/4 0 Adding 2 times row 1 to row 3 Adding -2 times row 1 to row 3 1 0 0 1 0 0 0 1 1 0 2 0 1 0 0 0 1 1= ?3 ?3= 2

7. RREF v.s. Elementary Matrix Let A be an mxn matrix with reduced row echelon form R. ?? ?2?1? = ? There exists an invertible m x m matrix P such that PA=R ? = ?? ?2?1 1 1?2 1 ?? ? 1= ?1

8. Invertible An n x n matrix A is invertible. R=RREF(A)=In ?? ?2?1? = ?? The reduced row echelon form of A is In 1?? 1?2 1 ?? ? = ?1 1 1?2 1 ?? = ?1 A is a product of elementary matrices