Polygon Armchair | Occasional Chairs | Collective Melbourne
Buy Polygon Armchair allows you a complete custom transformation by selecting from Prostoria\u2019s wide range of fabrics, leathers & metal frame finish from Collective, Melbourne's premier luxury furniture makers. Visit Us Now!\n
1 views • 2 slides
Understanding Spherical Mirrors: Concave and Convex Types, Image Formation, and Practical Uses
Spherical mirrors, including concave and convex types, play a crucial role in reflecting light. By exploring the properties of concave and convex mirrors, understanding image formation, and discovering their diverse applications in daily life, we can grasp the significance of these mirrors in scienc
0 views • 9 slides
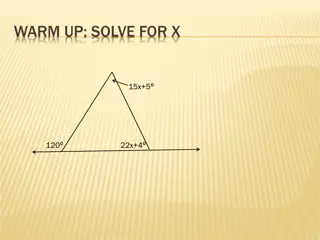
Exploring Polygon Angles in Geometry
Explore the interior and exterior angle measures of polygons, understand theorems related to polygon angles, classify polygons based on their properties, and solve problems involving regular polygons in this geometry chapter slideshow. The content covers key concepts such as the sum of interior angl
1 views • 41 slides
Discovering Geometry and Measurement Concepts in Grade 9 Mathematics
Explore the fundamentals of geometry and measurement in grade 9 math, covering topics such as regular polygons, congruence and similarity of triangles, construction of similar figures, trigonometric ratios application, circle properties, and problem-solving related to triangles and parallelograms. U
0 views • 17 slides
Polygon Clipping Techniques and Algorithms
Polygon clipping involves modifying line-clipping procedures to achieve bounded areas after clipping. The Sutherland-Hodgman algorithm is commonly used, where polygon boundaries are processed against window edges to generate closed areas for appropriate area fill. This process involves testing for v
1 views • 17 slides
Understanding Exterior Angles in Polygons
This content explains the concept of exterior angles in polygons and the Exterior Angle Theorem. It covers how exterior angles are formed when the sides of a polygon are extended, their relationship with interior angles, and how to calculate their measures using the Exterior Angle Theorem. Various e
2 views • 26 slides
Filling Polygons Using Scan Line Algorithm
Learn how to fill polygons using the Scan Line Algorithm, which involves intersecting scan lines with polygon edges and filling the area between intersections. Steps include finding Ymin and Ymax, intersecting scan lines with edges, sorting intersection points, and filling the interior of the polygo
0 views • 36 slides
Understand Convex and Concave Functions in Mathematics
Learn about convex and concave functions in mathematics, including how to differentiate between them, identify their characteristics, and analyze gradients. Explore the concepts with practical examples and visual aids. Enhance your proficiency in answering questions related to convex and concave fun
0 views • 15 slides
Generalization of Empirical Risk Minimization in Stochastic Convex Optimization by Vitaly Feldman
This study delves into the generalization of Empirical Risk Minimization (ERM) in stochastic convex optimization, focusing on minimizing true objective functions while considering generalization errors. It explores the application of ERM in machine learning and statistics, particularly in supervised
0 views • 11 slides
Optimization Techniques in Convex and General Problems
Explore the world of optimization through convex and general problems, understanding the concepts, constraints, and the difference between convex and non-convex optimization. Discover the significance of local and global optima in solving complex optimization challenges.
0 views • 24 slides
Closest Pair and Convex Hull: Brute Force Approach
Closest Pair Problem in 2D involves finding the two closest points in a set by computing the distance between every pair of distinct points. The Convex Hull Problem determines the smallest convex polygon covering a set of points. Dr. Sasmita Kumari Nayak explains these concepts using a brute-force a
0 views • 15 slides
Understanding Convex Hulls in Computational Geometry
Convex hulls are a fundamental concept in computational geometry, representing the smallest convex shape that contains a set of points. The process involves defining the convexity of a set, determining the unique convex polygon, and computing the convex hull efficiently using algorithms. This conten
0 views • 9 slides
Algorithms: Convex Hull, Strassen's Matrix Multiplication, and More
Explore various divide-and-conquer algorithms including Convex Hull, Strassen's Matrix Multiplication, and Quickhull. Understand the concepts of Sorting, Closest Pairs, and Efficiency in algorithm design. Discover efficient techniques such as recursive calculations and simplifications to enhance alg
1 views • 20 slides
Understanding Regular Polyhedra and Polygons
Regular polygons and polyhedra are fundamental shapes in geometry. A regular polygon has sides and angles that are congruent, such as equilateral triangles and squares. Polygons are simple closed figures made with line segments. Polyhedra are solids bounded by polygons as faces. Regular polyhedra ar
0 views • 18 slides
Understanding Nucleation Sites in MatCalc Simulations
Nucleation sites of precipitates in MatCalc simulations are crucial for understanding the nucleation rate, available sites, interfacial energy models, and more. This analysis delves into the consequences and special cases of nucleation, including factors such as dislocation density, grain boundaries
0 views • 32 slides
Insights into Recent Progress on Sampling Problems in Convex Optimization
Recent research highlights advancements in solving sampling problems in convex optimization, exemplified by works by Yin Tat Lee and Santosh Vempala. The complexity of convex problems, such as the Minimum Cost Flow Problem and Submodular Minimization, are being unraveled through innovative formulas
1 views • 47 slides
Convex Optimization: Interior Point Methods Formulation
This chapter on interior point methods in convex optimization explores the formulation of inequality-constrained optimization problems using barrier methods and generalized inequalities. It covers primal-dual interior point methods and discusses issues such as exponential complexity and determining
0 views • 24 slides
Understanding Areas of Regular Polygons
Explore the definitions, formulas, and theorems related to regular polygons, including central angles, apothems, and perimeter calculations. Learn how to find the area of a regular polygon through examples and solutions.
0 views • 11 slides
Exploring Links Between Convex Geometry and Query Processing
Delve into the intersection of convex geometry and query processing at Stanford University, where theoretical discussions are being applied to real-world database engine development. Learn about the optimization of database joins, the historical evolution of database engines, and the challenges face
0 views • 54 slides
Optics Solved Problems: How to Solve for Focal Lengths
This content provides solutions to various optics problems involving thick lenses, double convex lenses, bi-convex lenses, compound lenses, and more. It covers topics such as identifying principal and focal points, calculating image distances, determining the effective focal length of lens systems,
0 views • 12 slides
Frequency Finder 6 Mapping Workshops Overview
Explore the Frequency Finder 6 Mapping, Export, and Special Functions workshops held in Egypt and Thailand in October 2016. The workshops cover topics such as mapping station coverage, exporting data to different formats, accessing historical frequency assignment records, and ensuring data integrity
0 views • 7 slides
Understanding Polygons in Geometry
Explore the concept of polygons, their sides, vertices, and angles, and learn to classify them as convex or concave. Discover the Polygon Angle Sum Theorem and find the sum of measures of angles in a given polygon.
0 views • 13 slides
Exploring Quadrilaterals in Mathematics Education
This educational content delves into the understanding of quadrilaterals in mathematics, covering topics such as polygons, convex and concave shapes, regularity, diagonals, and angle properties. Through detailed explanations and visual aids, viewers can grasp the fundamental concepts and properties
0 views • 20 slides
Understanding Polygon Properties and Classification
Explore the fundamental concepts of polygons, such as vertices, sides, angles, and classifications like convex and concave polygons. Learn about the interior and exterior angles of polygons, the sum of angle measures, and the properties of regular polygons. Discover how to identify, classify, and ca
0 views • 13 slides
Understanding Fill Area Primitives in Computer Graphics
An overview of fill area primitives in computer graphics, including the concept of fill areas, polygon fill areas, and polygon classifications into convex and concave polygons. This module covers the efficient processing of polygons, approximating curved surfaces, and generating wire-frame views of
0 views • 63 slides
Raster Graphics and Scan Conversion in Computer Graphics
This lecture covers various topics related to raster graphics and scan conversion in computer graphics. It includes issues with scan converting a line, generalized line drawing algorithms, and the midpoint circle drawing algorithm. Additionally, it explores deriving mathematical expressions for draw
0 views • 21 slides
Exploring Geometric Concepts in Grade Five Mathematics
Dive into the world of geometry with Grade Five Mathematics! This module covers topics such as shapes classification, properties of two-dimensional and three-dimensional shapes, coordinate systems, polygon construction, and Van Hiele levels of geometric thought. Engage with hands-on activities, visu
0 views • 52 slides
Advanced Subpath Algorithms for Convex Hull Queries
This study presents innovative algorithms for subpath convex hull queries, focusing on efficient computation of convex hulls for subpaths between two vertices on a simple path in the plane. The work includes a comparison with previous methods, showcasing improvements in space complexity and query pr
0 views • 19 slides
Understanding Convex Hulls in Computational Geometry
Convex hulls play a vital role in computational geometry, enabling shape approximation, collision avoidance in robotics, and finding smallest enclosing boxes for point sets. The convex hull problem involves computing the smallest convex polygon containing a set of points, with extreme points determi
0 views • 119 slides
Geometry Chapter 6 Review Questions and Solutions
Explore a set of geometry review questions involving interior and exterior angles, polygon properties, parallelograms, trapezoids, and more. Test your knowledge and enhance your understanding of geometric concepts with these interactive problems.
0 views • 20 slides
Comprehensive Geometry Vocabulary Guide
This comprehensive geometry vocabulary guide covers essential terms related to 2-dimensional and 3-dimensional shapes, angles, attributes, and more. Explore definitions and examples of various geometric concepts like circle, cone, cube, cylinder, diagonal, hexagon, polygon, and more, accompanied by
0 views • 4 slides
Optimizing Multi-Party Video Conferencing through Server Selection and Topology Control
This paper proposes innovative methods for multi-server placement and topology control in multi-party video conferences. It introduces a three-step procedure to minimize end-to-end delays between client pairs using D-Grouping and convex optimization. The study demonstrates how combining D-Grouping,
0 views • 13 slides
GCSE Constructions and Loci Techniques
Explore a comprehensive guide to GCSE constructions and loci by Dr. J. Frost, covering topics such as triangle constructions, perpendicular bisectors, angle constructions, and polygon construction using basic tools like a straight edge and compass. Learn essential skills for precise geometric drawin
0 views • 35 slides
Understanding Polygon Angle-Sum Theorems
Explore the Polygon Angle-Sum Theorems that determine the sum of interior angle measures in polygons. Learn about the Polygon Angle-Sum Theorem, number of sides in polygons, finding angle sums, and the corollary for regular polygons. Practice using the theorems to calculate interior angle measures i
0 views • 18 slides
Understanding Polygon Angles and Theorems
Explore the angles of polygons, including interior and exterior angle sums, theorems 3-13 and 3-14, properties of regular polygons, and measurements of angles in various polygon types. Discover the relationships between sides, vertices, and angles to deepen your geometric knowledge.
0 views • 18 slides
Geometry Fundamentals: Theorems and Concepts Explained
Explore essential concepts in geometry such as solving equations, perpendicular transversal theorem, triangle exterior angle theorem, angle sum theorems, polygon classification, and naming polygorgons. Learn about the interior and exterior angles of triangles and why they add up to specific measurem
0 views • 21 slides
Exploring the Graphics Library for Enhanced User Interaction in Python
Explore the Zelle graphics library in Python for creating interactive graphical user interfaces. Learn about classes like GraphWin, Point, Line, Circle, Rectangle, Oval, Polygon, Text, Entry, and Image to enhance the visual appeal of your programs and engage users in a more intuitive manner. Utilize
0 views • 25 slides
Understanding the Shoe Lace Method for Finding Polygon Areas
The Shoe Lace Method is a mathematical process used to determine the area of any polygon by employing coordinate geometry. By following specific steps, including organizing coordinates, multiplying diagonally, and adding columns in a certain manner, the method allows for a straightforward calculatio
0 views • 8 slides
Calculating Polygon Area and Trapezium Area with Known Coordinates
The content above guides you on finding the exact area of a polygon by calculating the areas of individual triangles within it. It also demonstrates how to list coordinates in a spreadsheet, calculate the area of trapeziums formed by pairs of coordinates, and sum their areas to determine the total a
0 views • 28 slides
Coordinate-based Polygon Area Calculation Method
Utilize a step-by-step approach to determine the area of a polygon by listing coordinates in columns, calculating trapezium areas, and summing them up. This versatile method can be applied to any polygon, not limited to triangles.
0 views • 32 slides