Exploring Curve Fitting and Regression Techniques in Neural Data Analysis
Delve into the world of curve fitting and regression analyses applied to neural data, including topics such as simple linear regression, polynomial regression, spline methods, and strategies for balancing fit and smoothness. Learn about variations in fitting models and the challenges of underfitting and overfitting in statistical analysis.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Curve Fitting Variations and Neural Data Julie Michelman Carleton College Jiaqi Li Lafayette College Micah Pearce Texas Tech University Advisor: Professor Jeff Liebner Lafayette College
Neurological Statistics Stimulant Neurons Spikes
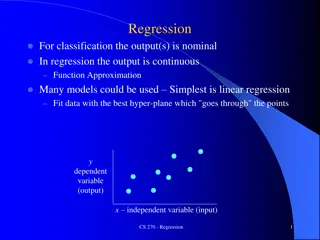
Simple Linear Regression Yi = 0 + 1 xi + i n = i 2 = ( ) RSS Y f x Minimize RSS: i i 1
Polynomial Regression Yi = 0 + 1 xi + 2 xi2 + 3 xi3 + i
An Alternative: Splines Spline: piecewise function made of cubic polynomials Partitioned at knots Evenly spaced or not
Balancing Fit and Smoothness Two alternative solutions Regression Splines Use only a few knots Question: How many knots and where? Smoothing Splines Penalty for overfitting Question: How much of a penalty?
Regression Splines Select a few knot locations Often chosen by hand, or evenly spaced
BARS - Bayesian Adaptive Regression Splines Goal: Find best set of knots Method: Start with a set of knots Propose a small modification Accept or reject new knots Repeat using updated knots Compute posterior mean fit Go to R for demo
Smoothing Splines Best fit minimizes PSS = i 1 n = + 2 2 ( ) [ ( )] [ ( ' ' )] PSS f Y f x f x dx i i 1st term distance between data and fitted function 2nd term penalty for high curvature weight of penalty
Large Smoother Fit Good on sides, underfits peak
Small More Wiggly Fit Captures peak, overfits sides
Smoothing Spline with Adjustable Given , best fit minimizes PSS n = i = + 2 2 ( ) [ ( )] [ ( ' ' )] PSS f Y f x f x dx i i 1 n = i = + 2 2 ( ) [ ( )] ( )[ ( ' ' )] PSS f Y f x x f x dx i i 1 But what is best , or best (x)?
Cross Validation (CV) Goal: minimize CV score n = i = 2 [ ( )] CV Y f x i i i 1 blue f i (x)
Cross Validation Ordinary smoothing splines: Define best as minimizing CV score Our solution: Define best (x) at xi as minimizing CV score near xi Combine local s into (x)
Local Lambda A graphic illustration Window size bandwidth = 31 points
Local Lambda A graphic illustration Lambda chosen by cross validation
Local Lambda A graphic illustration Key Red - True Function Black - Local Lambda Fit
Showdown!! Local Lambda Method Versus Regular Smoothing Spline
Step Function Key Blue - Constant Lambda Black - Local Lambda Fit
Mexican Hat Function Key Blue - Constant Lambda Black - Local Lambda Fit
Dopplers Function Key Blue - Constant Lambda Black - Local Lambda Fit
Conclusions Highly variable curvature: Local Lambda beats regular smoothing spline More consistent curvature: Regular smoothing spline as good or better Final Assessment: Local Lamba Method is successful! It is a variation of smoothing spline for that works for highly variable curvature.
Thank You Thanks to Gary Gordon for running the Lafayette College Math REU The National Science Foundation for providing funding Our advisors Jeff Liebner, Liz McMahon, and Garth Isaak for their support and guidance this summer Carleton and St. Olaf Colleges for hosting NUMS 2010 All of you for coming to this presentation!