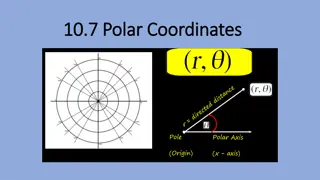
Deciphering Heavy Atom Coordinates from Difference Patterson Map: An Overview
Understanding how to determine heavy atom coordinates from a difference Patterson map involves recognizing the relationship between Patterson peak coordinates (u,v,w) and space group symmetry operators in crystallography. By solving equations that relate these coordinates, the absolute positions of heavy atoms can be found. Matching Patterson peaks to corresponding symmetry operators is crucial for obtaining accurate results.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
How to determine heavy atom coordinates from a difference Patterson map. An outline
Basic concepts If we observe a difference Patterson peak with coordinates (u,v,w), we learn that two atoms in the crystal are related by a vector with length u (along x), a length v (along y), and a length w (along z). In other words, the vector relating two atoms in the crystal has the magnitude and direction of a vector drawn from 0,0,0 to u,v,w. So, the Patterson peak coordinates tell us the relative positions of the two atoms, but not the absolute positions of the atoms. To determine the absolute positions of the atoms, we need to know the space group symmetry operator that relates the two atoms at the tips of the vector, u,v,w. If we can attribute the two atoms to space group symmetry operators, we can equate the difference between operators to u,v,w and solve for x,y,z. In order for this strategy to work, we must be confident that the two atoms are indeed related by crystal symmetry, and not both located within the same asymmetric unit. We are guaranteed this condition is met if each asymmetric unit contains only one heavy atom (as is true in our experiments). All peaks that we observe in our difference Patterson maps today have arisen from atoms related by crystallographic symmetry (i.e. operations that relate one asymmetric unit to another). So Patterson peak coordinates (u,v,w) specify a vector between space group symmetry-related atoms. If, for example, we also know that the crystal belongs to space group P21, then we know this vector has its tail at position x,y,z and its head at position -x,y+ ,-z. These are the only two symmetry operators in the space group P21, so there is no ambiguity in assigning (u,v,w) to equal this difference vector (x,y,z) (-x,y+ ,-z), that is -2x, , -2z. Now, we set up the equivalence between the Patterson vector (u,v,w) and crystal vector -2x, , -2z, to get u=-2x, v= , w=-2z. We can plug in values of (u,v,w) that we observed in the Patterson map to solve for x and z (y remains ambiguous). That s it! You solved the heavy atom structure. To approach the same problem graphically (rather than algebraically), we recognize this symmetry operation is a 2-fold screw axis along the y axis. We need to find a value of x and z that will produce the required symmetry mate at x and z while satisfying the requirement that the atoms in the crystal are related by distance u (along x), a distance v (along y), and a distance w (along z). The answer, as we already know, is to split u and w in half, giving x=u/2, and z=w/2. Knowledge of the space group symmetry offers us the ability to express Patterson peak coordinates as differences between space group symmetry operators.
Clues to assigning Patterson peaks to their corresponding symmetry operators In summary, we determine the x,y,z coordinates of the heavy atom by solving an equation relating coordinates u,v,w (Patterson space) to a pair of symmetry operators (in crystal space). The u,v,w coordinates of the Patterson peak describe the magnitude and direction of vector between a particular pair of atoms. The two symmetry operators describe the absolute position of the atoms located at the head and tail of the vector. We plug in values of u,v,w from the Patterson peak and solve for the x,y,z values for the atoms using algebra. In order for this method to be valid, it is important we match the Patterson peak to the to its corresponding difference vector. If we mismatch the peak to an unrelated pair of symmetry operators, the equivalence is invalid, and we will not obtain the correct value of x,y,z. Matching a Patterson peak to its corresponding difference vector requires making a choice. In general there are many ways to make an incorrect match, but only a few correct matches. If there is only one heavy atom in the asymmetric unit, then there are n2peaks in the Patterson map, where n is the number of symmetry operators in the space group. That is, one peak for every pair of heavy atoms in the unit cell. Of these n2peaks, n will be located at the origin of the Patterson map, and are uninformative. If we eliminate the redundancy arising from the fact that each atom pair produces a peak for both a forward and reverse vector, the number of uniquely informative peaks (and corresponding difference vector expressions) is reduced to (n2-n)/2. For a space group with 4 symmetry operators, like P21212, that means 6 Patterson peaks. If you are given a list of 6 Patterson peaks, how will you match each to its corresponding difference vector? Clues to matching a Patterson peak to its corresponding difference vector lies in noting which plane contains the peak. For example, if you see a peak lying somewhere on the v= plane, it can be confidently assigned to atoms related by a 21screw axis along y. This assertion is justified by realizing that the difference between symmetry equivalent positions x,y,z and -x,y+ ,-z specifies the peak be located at -2x, , -2z, which we recognize confines the peak to somewhere in the plane v= . In general, peaks arising from any rotational or screw axes are confined to such planes, called Harker sections. That is, Harker sections are planes of the Patterson map known to harbor peaks arising from rotational and screw axes. In practice, we systematically locate all the Harker sections for our space group of interest by subtracting x,y,z from each of the space group symmetry operators. Harker sections are indicated whenever the difference between symmetry operators produces a constant as one of the coordinates. For example, in space group P21212, there are 4 symmetry operators: (1) x,y,z (2) x,-y,z (3) x+ , y+ ,-z (4)x+ ,-y+ , -z. Subtracting x,y,z from each operator gives (op2-op1) -2x,-2y, 0 (op3-op1)-2x+ , , -2z (op4-op1) ,-2y+ , -2z. Thus, we find Harker sections at w=0, v= , and u= . So, if you see a Patterson peak somewhere on v= , you can have some confidence that it can be correctly assigned to the difference vector (op3-op1)-2x+ , , -2z. Equate the Patterson peak coordinate (u, ,w) to -2x+ , , -2z and solve for x and z.
How to obtain all 3 dimensions of an atomic coordinate (x,y,z) by combining info from 2 Harker sections A single Harker section is often insufficient to produce all 3 dimensions of a coordinate, x, y, and z. In the previous example, we were able to calculate x and z, but we have no value for y. In general, a Harker section provides only two of the three dimensions (x, y, and z) required to specify an atomic coordinate. The simplest way to obtain the 3rd dimension of the heavy atom coordinate is to evaluate the heavy atoms coordinates from another Harker section (perpendicular to the previous Harker section), and then combine two dimensions from the previous section with the 3rd dimension from the current Harker section. Each Harker section will yield two dimensions of x,y,z. Therefore, we will obtain two values for one of the dimensions in common between Harker sections. The numerical values obtained for the one dimension in common may or may not match each other. In the fortuitous case of space group P21212, we can ignore a mismatch in values of the common dimension. We may select either of the calculated values of the common dimension, and combine it with the calculated values of the remaining two dimensions to get a valid x, y, and z coordinate. This freedom is NOT allowed in the space group of proteinase K, P43212. In general, there are multiple valid choices of the numerical values of the heavy atom. A list of all valid x,y,z values can be generated by applying Cheshire symmetry operators to one validated choice of x,y,z. A look at the list of valid x,y,z values in space group P21212 reveals 64 alternatives. Note how each numerically distinct value of x in the list appears in combination with each distinct value of y and each distinct value of z. In space group P43212, atomic coordinate dimensions evaluated from different Harker sections can be combined only if the common value is numerically identical. If the two numerical values obtained for the common dimension are not equal, apply a Cheshire operator to both dimensions obtained from one Harker section (e.g. x and z), then combine with the dimensions e.g. (x and y) evaluated from the other Harker section.
How to verify your x,y,z answer is consistent with space group P43212. The correct hand of the heavy atom substructure cannot be distinguished using Patterson methods. All Patterson maps contain a center of inversion, meaning heavy atom coordinates x,y,z and -x,-y,-z equally well predict the positions of peaks u,v,w in the Patterson map. However, only one hand is correct, and it will be identified later by comparing the maps phased by each choice of hand. In most space groups, like P21212, both hands of the heavy atom substructure are consistent with the space group symmetry. So space group operators of P21212 may be used to calculate maps from both hands of the heavy atom substructure. However, space group P43212 is special because it has a handedness. The 43 axis is a left handed screw. The mirror image of this space group is P41212 , in which 41 is a right handed screw. One hand of the heavy atom substructure is compatible with P43212 only, and the opposite hand is compatible with P41212 only. This division imposes an additional task for us to sort out whether our heavy atom solution is compatible with P43212 or P41212. We have a strategy to sort out which space group is consistent with our values of x,y,z. We will use a pair of P43212 symmetry operators to predict the u,v,w coordinate of a Patterson peak. If we find this peak, we can be certain the heavy atom solution is consistent with P43212. If we cannot find this peak (even after applying Patterson symmetry operators), it probably means the heavy atom solution is consistent with P41212. If this is the case, we recommend inverting the hand of the heavy atom solution by negating x to make it compatible with P43212.