Understanding Polar Coordinates in Mathematics
Polar coordinates define the location of a point in terms of distance and angle from an origin. The distance is denoted by "r" and the angle by "?". However, the angle is not unique for a point. The concept involves fixing an origin and an initial ray, with positive angles measured counterclockwise. Points can have multiple representations based on different angles. Polar equations involve tracing circles or lines based on fixed or varying values of "r" and "?". Understanding polar coordinates is essential for various mathematical applications.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
POLAR COORDINATES POLAR COORDINATES Ms. Nirusha Shetty Asst. Professor Dept. of Mathematics
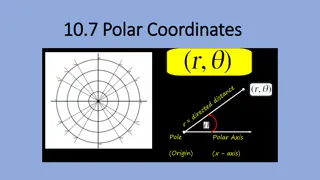
Polar coordinates : To define polar coordinates fix an origin 0 (called pole) and an initial ray from 0. Then each point P has polar coordinates (r,?) in which r gives the directed distance from 0 to P and ? gives the directed angle from the initial ray OX to ray OP. P(r, ?) 0 initial ray X origin (pole)
Note : ? is +ve when measured counter clockwise (anticlockwise) and ve when measured clockwise. The angle associated with a given point is not unique. For example : The point 2 units from the origin along the ray =? as polar coordinates r = 2, =? 6also it has polar coordinates r = 2, = 11? 6 6
P(2, ? 6)= P(2, 11? 6)
Some times r is ve For example : Point P(2, 7? anticlockwise from the initial ray and going farward 2 units. It can also be reached by turning ? 6radian counter clockwise 2 units. So the point also has the polar coordinates r = -2, =? 6) can be reached by turning 7? 6radians 6
Polar equations : If we hold r fixed at a constant value say r = a 0, the point P(r, ?) will lie |?| units from the origin 0. As ? varies over 0 to 2?, P then traces a circle of radius |?| centred at 0. r = a |?| x 0
If we hold ? fixed at constant value, say ? = ?0 and let r vary between ?? . The point P(r, ?) traces the line through 0 that makes an angle of measure ?0 with the initial ray. ? = ?0 0 x