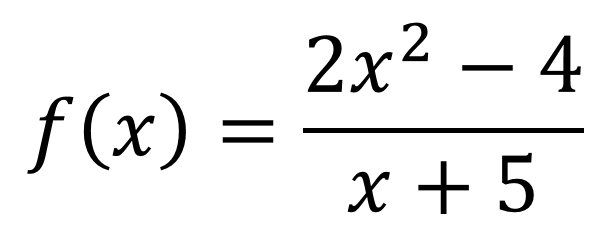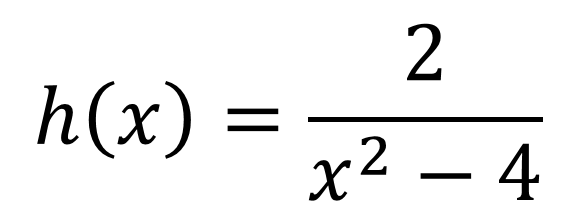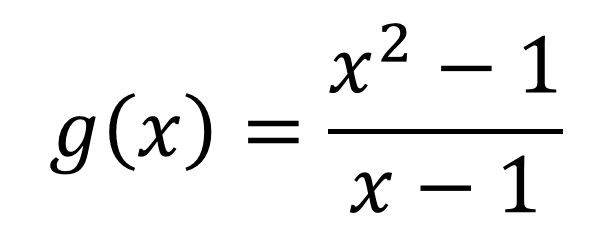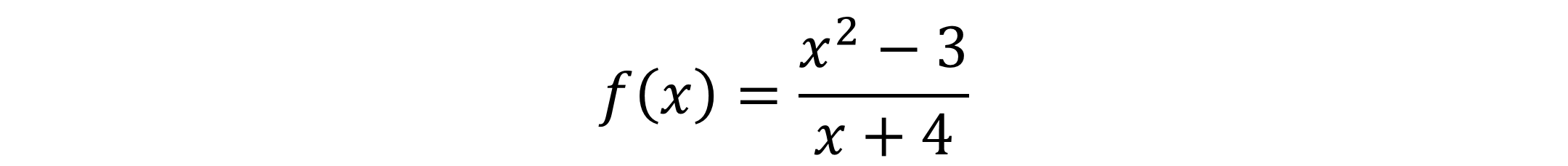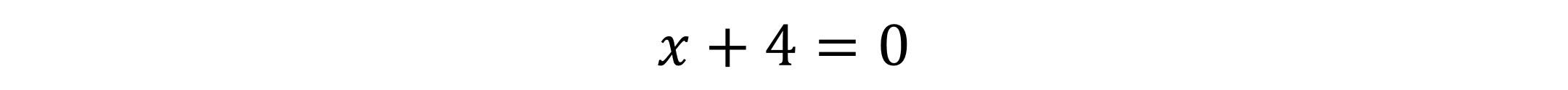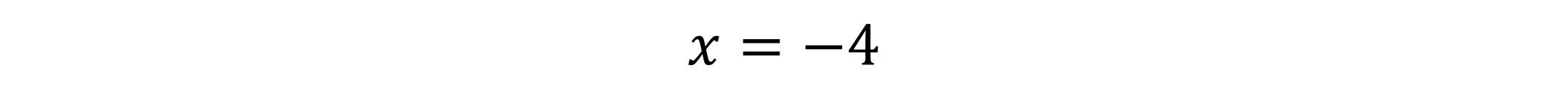Understanding Properties of Rational Functions
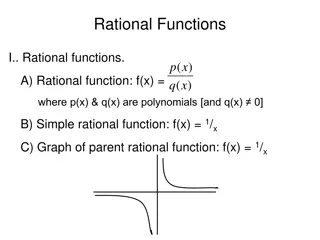
Rational functions are expressed as the ratio of two polynomials. The domain of a rational function excludes values that make the denominator zero. Various examples illustrate how to determine the domain and identify asymptotes in rational functions. Vertical asymptotes exist where the denominator is zero but not the numerator. This content provides insights into the properties of rational functions and how to interpret them graphically.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Section 5.2 Properties of Rational Functions Defn: Rational Function A function in the form: ? ? =?(?) ?(?) The functions p and q are polynomials. The domain of a rational function is the set of all real numbers except those values that make the denominator, q(x), equal to zero. ? ? =?2 1 ? ? =2?2 4 2 ? = ?2 4 ? 1 ? + 5
Section 5.2 Properties of Rational Functions Domain of a Rational Function ? ? =?2 3 ? + 4 ? + 4 = 0 ? = 4 ??????: {x | x 4} or (- , -4) (-4, )
Section 5.2 Properties of Rational Functions Domain of a Rational Function ? ? =?2 4 ? 2 ? 2 = 0 ? = 2 ??????: {x | x 2} or (- , 2) (2, )
Section 5.2 Properties of Rational Functions Domain of a Rational Function 2 ? = ?2 9 ?2 9 = 0 (? 3)(? + 3) = 0 x = 3,3 ??????: {x | x 3, 3} or (- , -3) (-3, 3) (3, )
Section 5.2 Properties of Rational Functions Domain of a Rational Function 2? + 3 ?2 2? 15 ? = ?2 2? 15 = 0 (? 5)(? + 3) = 0 x = 3,5 ??????: {x | x 3, 5} or (- , -3) (-3, 5) (5, )
Section 5.2 Properties of Rational Functions Linear Asymptotes (vertical, horizontal, or oblique) Lines in which a graph of a function will approach. By approach we mean each successive value of X puts the graph closer to the asymptote than the previous value. Vertical Asymptote A vertical asymptote exists for any value of x that makes the denominator zero AND is not a value that makes the numerator zero, in this case the factors would cancel. Example =(? 4)(? + 4) ? + 5 ? ? =?2 16 x = 5 ? + 5 VA: ? = 5 A vertical asymptotes exists at x = -5.
Section 5.2 Properties of Rational Functions Asymptotes Vertical Asymptote Example =(? + 2)(? 3) (? 4)(? 3) ?2 ? 6 ?2 7? + 12 x = 3,4 ? ? = A vertical asymptote exists at x = 4. VA: ? = 4 A vertical asymptote does not exist at x = 3 as it is a value that also makes the numerator zero. A hole exists in the graph at x = 3.
Section 5.2 Properties of Rational Functions Asymptotes Horizontal Asymptote A horizontal asymptote exists if the largest exponents in the numerator and the denominator are equal, or if the largest exponent in the denominator is larger than the largest exponent in the numerator. If the largest exponent in the denominator is equal to the largest exponent in the numerator, then the horizontal asymptote is equal to the ratio of the coefficients. If the largest exponent in the denominator is larger than the largest exponent in the numerator, then the horizontal asymptote is ? = 0.
Section 5.2 Properties of Rational Functions Asymptotes Horizontal Asymptote Example ? ? =5?3 2?2 7 2?3 7? + 10 HA: ? =5 A horizontal asymptote exists at y = 5/2. 2 ? 6 ? ? = ?2 7? + 12 HA: ? = 0 A horizontal asymptote exists at y = 0.
Section 5.2 Properties of Rational Functions Asymptotes Oblique (slant) Asymptote An oblique asymptote exists if the largest exponent in the numerator is one degree larger than the largest exponent in the denominator. **Note** Other non-linear asymptotes can exist for a rational function.
Section 5.2 Properties of Rational Functions Asymptotes Oblique Asymptote Example An oblique asymptote exists. Long division is required. We ignore the remainder if it exists ? ? =?2+ 1 ? ? + x + 2 0 1 x x ?2 0 0? An oblique asymptote exists at y = x. OA: ? = ?
Section 5.2 Properties of Rational Functions Asymptotes Oblique Asymptote Example ? ? =4?4+ 2?2+ ? 1 2?3+ 3? An oblique asymptote exists. Long division is required. 2? + + + + + + 4?2 + + 3 4 3 2 2 x 3 x 4 4?4 x 0 x 2 6?2 x x 1 An oblique asymptote exists at y = 2x OA: ? = 2?