Understanding Points of Discontinuity in Rational Functions
Explore the concept of points of discontinuity in rational functions, where the denominator equals zero, leading to breaks in the graph. Learn about types of discontinuities such as vertical asymptotes and holes, and discover how to identify them in graphical representations through examples.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
POINTS OF DISCONTINUITY
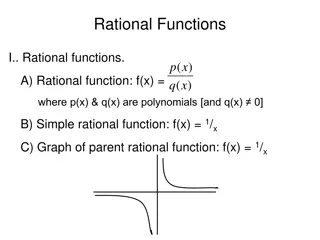
Rational Function Rational Function f(x) is a function that can be written as ( ) ( ) P x Q x ( ) f x ( ) ( ) = , P x and Q x are where ( ) polynomial functions and Q x 0
Points of Discontinuity a) A graph is continuous if no value of x makes the denominator zero, so it has no breaks. b) A graph is discontinuous if it contains a REAL number which produces zero when substituted into the denominator. A point of discontinuity is a RESTRICTION; where the denominator equals zero because it breaks the graph at that point.
Look at the graph and find where the denominators would be restricted. ? = 2, 2
Example 1: Finding points of discontinuity. 3 x 2x .) y= a b.) y = + 2 2 x 12 3x 4 (? 4)(? + 3) ? 4, 3 None No REAL root
2 Types of Discontinuity: Vertical Asymptotes(x =) and Holes a. A POD is a vertical asymptote if it does NOT cancel out with any common factor in the numerator. (Draw asymptotes with dashed lines) b. If the POD DOES cancel out with a common factor then there is a hole in the graph. (Holes are a point! Write them (x, y). Note: A vertical asymptote COVERS a hole if they overlap.
Example 2: Finding Vertical Asymptotes and Holes + + 2 x 3 3 x-7 x .) y= a b.) y = ( )( ) x+ x+1 5 x ? =? ? + 3 ? + 3 ? = 1, 5 These are both ?? ??? ?? ? = 3 To find ?,plug ? into the SIMPLIFIED equation: ? = ? ??? @ ( 3, 3)
Example 2: Finding Vertical Asymptotes and Holes + 2 x x 3 54 x ? + 9 ? 6 ? + 92? 6 c.) y = ? = ( ) ( ) 2 + 9 6 x 1 ? = ? + 9 ???:? = 6 ??: ? = 9 ???: 6,1 15 ??: ? = 9 ? ? ??? ?? ? = 9 ?? ??????? ?? ? ? ???????? ?????????
Example of a hole in the graph, y =(x-5)(x+2) (x-5) ? = ? + 2 ???:? = 5 (5,7)
Horizontal Asymptotes (y=) DIVIDE the LC of the numerator by the LC of the denominator a) ? =3?2+? 2 b) ? =?3+6 ?3 3 6?2+3? ? =1 ? = 1 2 5? 1 2?3+4d) ? =?2 ? ? = 0 c) ? = ?+1 ????
Example 3: Find the HA of each function. 2 x + + + 4 2 3 1 x x = ) y = a ) b y 2 x None ? = 2 + 3 x x = ) y c ? = 0 ( )( ) + 1 4 x
Example 3 Find the Horizontal Asymptotes + 2 2x x 5 x+1 .) y= e f.) y = ( )( ? = 0 ) + 2 4 ? = 2 x+2 3 x ( )( x ) 2x+3 3 2 1 x g.) y = None ( ) 2 + 3
Homework Page 495-496 # s 2-8 even, 10-16, 20-24 even
Horizontal Asymptotes (y=) a. If the degree of the denominator is greater than the degree of the numerator the horizontal asymptote is y = 0 b.If the degree of the numerator is greater than the degree of the denominator the graph has NO horizontal asymptote. c.If the degree of the denominator is equal to the degree of the numerator the horizontal asymptote is y =a b is the leading coefficient of the numerator and is the leading coefficient of the denominator. a b