Understanding Triangle Congruence Properties

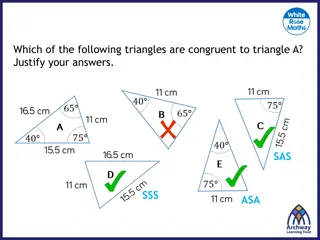
Delve into the principles of congruent triangles by exploring the properties of side-side-side (SSS), side-angle-side (SAS), angle-side-angle (ASA), and right-angle-hypotenuse-side (RHS) congruence. Visual explanations help clarify how these properties determine if triangles are congruent.

• Triangle Properties
• Congruent Triangles
• SSS
• SAS
• ASA

stetler_r Follow

Uploaded on Sep 15, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

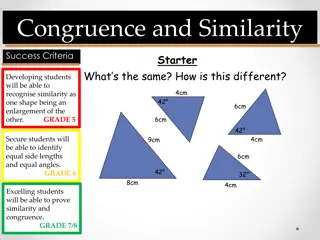
1. Starter What s the same? What s different? 4cm 42 6cm 6cm 42 4cm 9cm 6cm 42 32 8cm 4cm

2. Definitions Congruent shapes have all sides and angles equal. Similar shapes have all angles equal but one is an enlargement of the other.

3. Congruence Are these triangles congruent? For triangles to be congruent, three properties must be the same: SSS 6cm 4cm 6cm 3.5cm 4cm 3.5cm

4. Congruence Are these triangles congruent? For triangles to be congruent, three properties must be the same: SAS 4cm 3.5cm 78 78 4cm 3.5cm

5. Congruence Are these triangles congruent? For triangles to be congruent, three properties must be the same: ASA 4cm 47 78 47 78 4cm

6. Congruence Are these triangles congruent? For triangles to be congruent, three properties must be the same: RHS 5cm 5cm 4cm 4cm

7. Are these triangles congruent?

8. Are these triangles congruent?

9. Are these triangles congruent?

10. Are these triangles congruent?

11. Are these triangles congruent?

12. Are these triangles congruent?

13. Are these triangles congruent?

14. Are these triangles congruent?

15. Are these triangles congruent?

16. P Diagram NOT accurately drawn Triangle PQR is isosceles with PQ = PR. X is a point on PQ. Y is a point on PR. PX = PY. Prove that triangle PQY is congruent to triangle PRX (Total 3 marks) Y X R Q PX = PY (as in question) PR = PQ (isosceles triangle) Angles RPQ = QPR (same angle) SAS proves triangles are congruent.

17. Answers Work in pairs using the answers to decide how many marks you would award yourself for each question.

18. Plenary Create your own question on proving congruence or similarity. Make sure you have provided enough information on your diagram.