Understanding Congruent Triangles in Geometry
This content delves into the concept of congruent triangles in geometry, providing definitions, examples, and guidance on proving triangles congruent using various methods such as SSS, SAS, ASA, and AAS. Through images and step-by-step explanations, learners can enhance their understanding of triangle congruence and sharpen their proof-writing skills.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Notes Lesson 5.2 Congruent Triangles Target 4.1 help Right_arrow left_arrow HELP GEOMETRY HELP
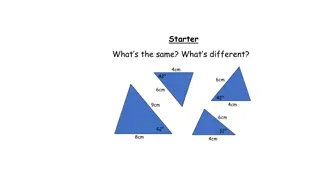
Congruent Figures Lesson 5.2 Definition: Congruent triangles are triangles that have all corresponding sides congruent and all corresponding angles congruent. Write a congruence statement for the triangles at the left. What information is sufficient to prove triangles congruent? help Right_arrow left_arrow HELP GEOMETRY HELP
Congruent Figures Target 4.1 Example 2: XYZKLM, YZ= x + 10 LM= 2x Find the value of x and the lengths of the given sides. Begin marking these triangles with corresponding angles that are congruent. help Right_arrow left_arrow HELP GEOMETRY HELP
Leading to Target 4.2 help Right_arrow left_arrow HELP GEOMETRY HELP
help Right_arrow left_arrow HELP GEOMETRY HELP
help Right_arrow left_arrow HELP GEOMETRY HELP
Triangle Congruence by SSS and SAS Lesson 5.3 help Right_arrow left_arrow HELP GEOMETRY HELP
Triangle Congruence by ASA and AAS Example 3: Write a two-column proof. Given: A B, APBP Prove: APXBPY 1 2 1 2 Statements A 1@ 2 Reasons , B AP 1. Given BP 1. 2. 2. Vertical angles are congruent. BPY APX 3. 3. ASA help Right_arrow left_arrow HELP GEOMETRY HELP
Triangle Congruence by ASA and AAS Example 4: TARGET 4.3 & 4.5 Given 2 Not an included side 1 Write a two-column proof that uses AAS. Given: B D, AB || CD Prove: ABCCDA Statements Reasons 1. B D, AB || CD 2. 1 2 3. ACCA 1. Given 2. If lines are ||, then alternate interior angles are . 3. Reflexive Property of Congruence 4. ABCCDA 4. AAS Theorem help Right_arrow left_arrow HELP GEOMETRY HELP
Triangle Congruence by SSS and SAS Target 4.2 Example 5: Copy the diagram. Mark the congruent sides. Given:M is the midpoint of XY, AXAY Prove: AMXAMY From the given information, can you prove that the triangles are congruent. Explain. Midpoint M implies MXMY. AMAM by the Reflexive Property of Congruence. AMXAMY by the SSS Postulate. help Right_arrow left_arrow HELP GEOMETRY HELP
Triangle Congruence by SSS and SAS Target 4.2 Example 6: A B a) Draw the two congruent triangles separately. a) D C C D b) DCCD by the Reflexive Property. You now have two pairs of corresponding congruent sides. Therefore if you know ADC BCD, you can prove ADCBCD by SAS. b) ADBC. What other information do you need to prove ADCBCD by SAS? help Right_arrow left_arrow HELP GEOMETRY HELP
TARGET 4.3 YOU TRY #1 help Right_arrow left_arrow HELP GEOMETRY HELP
Review: Right triangle: H L L Hypotenuse Leg H L L Leg TARGET 4.4 help Right_arrow left_arrow HELP GEOMETRY HELP
Congruence in Right Triangles TARGET 4.4 Example 7: What additional information is needed to prove. Prove: ABCDCB by HL. C C D B A B Since BCCB Reflexive Property of Congruence You must prove that BD CA To prove ABCDCB by the (HL Theorem). help Right_arrow left_arrow HELP GEOMETRY HELP
Congruence in Right Triangles TARGET 4.4 Example 8: One student wrote CPAMPA by SAS for the diagram below. Is the student correct? Explain. The diagram shows the following congruent parts. CAMA CPA MPA PAPA The congruent angles are not included between the corresponding congruent sides. The triangles are not congruent by the SAS Postulate, but they are congruent by the HL Theorem. help Right_arrow left_arrow HELP GEOMETRY HELP
YOU TRY #2 TARGET 4.4 What additional information will allow you to prove the triangles congruent by the HL theorem? A. S @ Q B. m RPQ = 90 C. SR @QP D. PR @ RS help Right_arrow left_arrow HELP GEOMETRY HELP
YOU TRY #3 TARGET 4.4 help Right_arrow left_arrow HELP GEOMETRY HELP