Exploring Triangle Similarity and Congruence
This content delves into understanding triangle congruence and similarity through various scenarios and visual representations. It discusses how to determine congruence using side-side-side, side-angle-side, and angle-side-angle criteria, and explores the concept of similarity in triangles based on equal corresponding angles. The content also covers construction of multiple triangles with given angles and sides, and highlights the similarities and differences between these geometric shapes.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
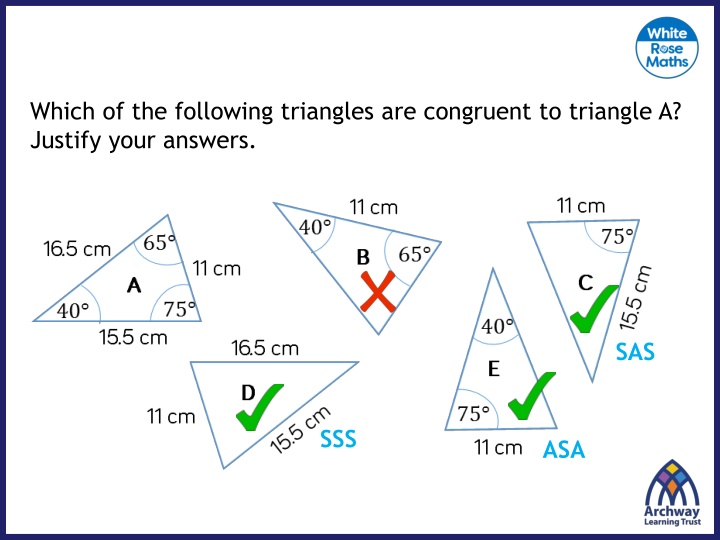
Which of the following triangles are congruent to triangle A? Justify your answers. SAS SSS ASA
What about AAA? Given three angles, is it possible to construct more than one triangle? How do we describe the relationship between these shapes?
Thinking back to previous work 1 How big is ? 30
Thinking back to previous work x 30 1 2 How big is x? How big is ? 30 4
Thinking back to previous work 8 x 4 30 y 4 1 2 How big is x? How big is y? How big is ? How big is ? 4 30 4 Discuss: What do you notice about these triangles? What is the same, what is different?
1. 2. 3. 4 ? ? ? 4 1 30 30 30 5. 6. 4. 2 ? 6 60 60 60 ? 6 ? 7. What do you notice about these triangles? What is the same, what is different? 6 30 ? ???????? ?????????? ??? ?? =? ???? = ?
1. 2. 3. ? = ? ? = ? 4 ? ? ? 4 1 ? = ? 30 30 30 5. 6. 4. ? = ?? 2 ? 6 60 60 60 ? 6 ? ? = ? ? = ? 7. What do you notice about these triangles? What is the same, what is different? 6 30 ? ???????? ?????????? ??? ?? =? ? = ? ???? = ?
What is similarity? The diagram shows two overlapping triangles. What makes the two shapes similar?
What is similarity? When two shapes are similar, their corresponding angles are equal.
How do you know the following overlapping triangles are similar?
How do you know the following overlapping triangles are similar? C C A D B B A E A E D
How do you know the following overlapping triangles are similar? A B C D E
Construct two similar triangles Draw two lines of different length (5cm & 10cm) Construct the same angles at each vertex (40 & 80 ) Continue the lines until they intersect. How big is the third angle? How long are the side lengths? Label the triangles A and B 5cm 10cm
Compare the corresponding lengths Length of side in triangle A Length of corresponding side in triangle B Can you spot a relationship between the sides?
Compare the corresponding lengths Shown below is another example of two similar triangles Length of side in triangle A Length of corresponding side in triangle B 3 4 5 12 16 20 Can you spot a relationship between the sides?
Compare the corresponding lengths Shown below is another example of two similar triangles Length of side in triangle A Length of corresponding side in triangle B 4.5 13.5 15 3 9 10 Can you spot a relationship between the sides?
What is similarity? When two shapes are similar, their corresponding angles are equal and the corresponding sides lengths have all enlarged by the same scale factor.
On your whiteboards: A and B are both right-angled scalene triangles, whilst C is isosceles. Look at the relationship between the side lengths.
On your whiteboards: B and C are in fact congruent!
On your whiteboards: B and C are both right-angled triangles, whilst A is isosceles. Look at the relationship between the side lengths.
On your whiteboards: B and C are both right-angled triangles, whilst A is scalene. Look at the relationship between the side lengths.