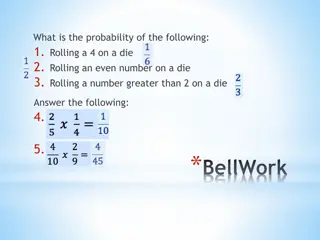Understanding Probability of Compound Events
Compound events involve multiple outcomes occurring together, such as independent events where one outcome does not affect another, and dependent events where one outcome affects the other. Complement sets, card probabilities, and mutually exclusive events are also discussed, providing a comprehensive overview of probability concepts.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
PROBABILITY OF COMPOUND EVENTS
COMPOUND EVENTS Made up of two or more events. Example: the probability that a flight will be on time & your luggage will arrive. Create your own compound event.
INDEPENDENT EVENTS The outcome of one event does NOT affect the outcome of the other. Equation: P(A and B) = P(A) x P(B) Symbol A n B Example 1 : A bag contains 6 black marbles, 9 blue marbles, 4 yellow marbles, and 2 green marbles. A marble is selected, replaced, and a second marble is selected. Find the probability of selecting a black marble, then a yellow marble.
Example 2: P(blue, green) Example 3: P(not black, blue)
DEPENDENT EVENTS The outcome of one event affects the outcome of another event. Equation: P(A and B) = P(A) x P(B following A) Example 4 : A bag contains 6 black marbles, 9 blue marbles, 4 yellow marbles, and 2 green marbles. A marble is selected, then a second marble is selected. Find the probability of selecting a black marble, then a yellow marble.
Example 5: P(blue, green) Example 6: P(not black or blue, blue)
COMPLEMENT OF A SET The set of all objects that do NOT belong to the given set. Example: The probability of drawing a heart & the probability of NOT drawing a heart. Create your own complement. The sum of these probabilities is ALWAYS 1 whole or 100%.
CARDS Total number of cards in a deck? ______ How many suits? _____ Name them. How many cards are in each suit? _____ How many cards of each face? _____ How many different face cards? Name them. How many of each color? _____
MUTUALLY EXCLUSIVE EVENTS Events that can NOT occur at the same time. Example: the probability of drawing a heart or a diamond. Equation: P(A or B) = P(A) + P(B) Symbol A u B Example 7: A die is being rolled. Find the probability of rolling a 3 or 5.
Example 8: P(at least 4) Example 9: P(less than 3)
NOT MUTUALLY EXCLUSIVE Events that CAN occur at the same time. Example: the probability of being on the honor roll, in the SADD club, or being both on the honor roll & in the club. Equation: P(A or B) = P(A) + P(B) P(A and B)
Example 10: Of 240 girls, 176 are on the Honor Roll, 48 play sports, and 36 are on the Honor Roll and play sports. What is the probability that a randomly selected student plays sports or is on the Honor Roll? Example 11: Out of 5200 households surveyed, 2107 had a dog, 807 had a cat, and 303 had both a dog and a cat. What is the probability that a randomly selected household has a dog or a cat?
REVIEW Draw a model to describe the following terms. Define each: Mutually Exclusive, Independent, Compound Events, Not Mutually Exclusive, & Dependent.
CIRCLE THE SAMPLE SPACE 1. What is the proportion of students who live in Currituck & are male? 2. What is the probability that a male student who passes Math II is also in the SADD Club?
NAME THREE DIFFERENT PROBABILITY MODELS 1. 2. 3. 4.