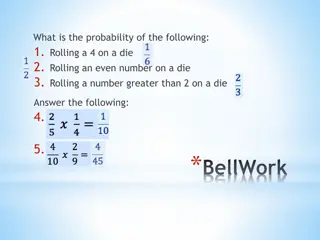Understanding Probability: Concepts and Applications
Probability is the likelihood of an event occurring, with theoretical probability based on all possible outcomes and experimental probability based on results. Events can be independent or dependent, impacting subsequent outcomes. Explore vocabulary, scenarios like rock-paper-scissors, and coin flipping to grasp fundamental probability concepts effectively.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Vocabulary Probability: the chance of an event happening or occurring. Theoretical Probability: It is the chances of an event happening based on all the possible outcomes. Ex: Tossing a Coin Experimental Probability: the chances of an event happening based on the result of an experiment. Independent Event: when an event occurs and has no affect on the occurrence of another event. Ex: Picking a card from a deck then a second card with replacement. Dependent Event: when an event occurs and affects the occurrences of the other event. Ex: Picking a card from a deck then a second card without replacement. Sample Space: all possible outcomes of an event. Event: the result of a single trial of an experiment.
For each of the following probabilities, write dependent if the outcome of the second event depends on the outcome of the first event independent if it does not. a. P(spinning a 3 on a spinner after having just spun a 2) [ Independent ] b. P(drawing a red 6 from a deck of cards after the 3 of spades was just drawn and not returned to the deck) [ Dependent ] c. P(drawing a face card from a deck of cards after a jack was just drawn and replaced and the deck shuffled again) [ Independent ] d. P(selecting a lemon-lime soda if the person before you reaches into a cooler full of lemon-lime sodas, removes one, and drinks it) [ Independent ]
Rotation #1 Rock, Paper, Scissors Rotation #1 Rock, Paper, Scissors a) Imagine that two people, Player A and Player B, were to play rock-paper-scissors 12 times. How many times would you expect Player A to win? Player B to win? What are the possible outcome of one trial? b) Now play rock-paper-scissors 12 times with a partner. Record how many times each player wins and how many times the game results in a tie. c) How does the experimental probability for the 12 games that you played compare to the theoretical probability that each of you will win? Do you expect them to be the same or different? Why?
Rotation #1 Rock, Paper, Scissors Rotation #1 Rock, Paper, Scissors a) Imagine that two people, Player A and Player B, were to play rock-paper-scissors 12 times. How many times would you expect Player A to win? Player B to win? What are the possible outcome of one trial? b) Now play rock-paper-scissors 12 times with a partner. Record how many times each player wins and how many times the game results in a tie. c) How does the experimental probability for the 12 games that you played compare to the theoretical probability that each of you will win? Do you expect them to be the same or different? Why?
Rotation#2: Flipping a Coin Rotation#2: Flipping a Coin a) How many possible outcomes are there when flipping a coin? b) What is the theoretical probability of flipping a head? A tails? c) In partners, record 10 trials of flipping a coin. Use H for heads and T for tails. d) What was the experimental probability for flipping a heads? Tails? e) How does the experimental probability for the 10 trials that you did compare to the theoretical probability? f) Do you expect them to be the same or different? Why? g) What do you predict would happen if we repeated this activity by using 50 trials? 100 trials? 1000 trials? etc.
Rotation#2: Flipping a Coin Rotation#2: Flipping a Coin a) How many possible outcomes are there when flipping a coin? b) What is the theoretical probability of flipping a head? A tails? c) In partners, record 10 trials of flipping a coin. Use H for heads and T for tails. d) What was the experimental probability for flipping a heads? Tails? e) How does the experimental probability for the 10 trials that you did compare to the theoretical probability? f) Do you expect them to be the same or different? Why? g) What do you predict would happen if we repeated this activity by using 50 trials? 100 trials? 1000 trials? etc.
Rotation#3: Rolling Dice Rotation#3: Rolling Dice A number cube numbered from 1 to 6 is rolled. Find the probability of each event below and express each as a fraction. P(1) = ________ P(a composite number) = ________ P(an even number) = ________ P(1, 2, or 3) = ________ P(not a 2) = ________ P(not an even number) = ________ P(3 or 4) = ________ P(not 2 or 5) = ________ P(8) = ________ P(a number less than 10) = ________
Rotation#3: Rolling Dice Rotation#3: Rolling Dice A number cube numbered from 1 to 6 is rolled. Find the probability of each event below and express each as a fraction. P(1) = ________ P(a composite number) = ________ P(an even number) = ________ P(1, 2, or 3) = ________ P(not a 2) = ________ P(not an even number) = ________ P(3 or 4) = ________ P(not 2 or 5) = ________ P(8) = ________ P(a number less than 10) = ________
Rotation#4: Cards Rotation#4: Cards a) How many cards are in a standard deck?(excluding jokers) b) How many suits are in a deck of cards? What are they? c) Find the theoretical probabilities for each situation: P(red card)=______ P(black card)=_____ P(7)= P(5)=_______ P(Queen or King)=________ P(Diamond)=_______ P(Ace)=________ P(Black AND King)=_______ P(three Queens in a row with replacement)=_____
Rotation#4: Cards Rotation#4: Cards a) How many cards are in a standard deck?(excluding jokers) b) How many suits are in a deck of cards? What are they? c) Find the theoretical probabilities for each situation: P(red card)=______ P(black card)=_____ P(7)= P(5)=_______ P(Queen or King)=________ P(Diamond)=_______ P(Ace)=________ P(Black AND King)=_______ P(three Queens in a row with replacement)=_____
Example #1 For Shelley s birthday on Saturday, she received: Two new shirts (one plaid and one striped) Three pairs of shorts (tan, yellow, and green) Two pairs of shoes (sandals and tennis shoes). On Monday she wants to wear a completely new outfit. How many possible outfit choices does she have from these new clothes?
Example #2 A radio station is giving away free t-shirts to students in local schools. It plans to give away 40 shirts at Big Sky Middle School and 75 shirts at High Peaks High School. Big Sky Middle School has 350 students, and 800 students attend High Peaks High School. a. What is the probability of getting a t-shirt if you are a student at the middle school? b. What is the probability of getting a t-shirt if you are a student at the high school? c. Are you more likely to get a t-shirt if you are a student at the high school, or at the middle school?
Example #3 A spinner is divided into 10 equal sections. 4 sections are pink, 2 are black, 1 is silver, 1 is gold, and 2 are white. Find the probability of each spin below and express each as a decimal. P(white) = ________ P(black) = ________ P(gold) = ________ P(silver or gold) = ________ P(not pink) = ________ P(not pink or silver) = ________ P(pink, black, or white) = ________ P(not silver or white) = ________ P(purple) = ________ P(pink) = ________
Example#4 Each of the 36 teens was asked which of 3 types of music (Rap, Rock, Country) the teen had listened to the day before. The survey results are given in the figure below. Rap 9 4 1 2 8 6 6 Rock Country Of the teens surveyed, 1 teen is selected at random. What is the probability that the teen answered with exactly 1 type of music?