Understanding Forces and Vectors in Statics with Air Balloon Models
Explore the world of forces and vectors in statics through the model of a hot air balloon. Learn about vectors of negative magnitude, zero, addition, subtraction, parallel and perpendicular components, and multiplying by a scalar. Discover how to find components and the resultant force of multiple forces using trigonometry. Dive into real-life situations where terms like air resistance, weight, and force resolution are applied.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
starter Jot down everything you know about VECTORS negative magnitude zero Add and subtract notation Parallel Perpendicular equal Multiply by a scalar
Statics Force diagrams Force Diagrams Hot air balloon Use trigonometry to find the components of a vector (or magnitude and direction) Find the resultant of two or more forces, as the sum of components Starter: think of a situation in real life that these terms would be used Air Resistance Weight Force resolving magnitude direction
Force diagrams intro 1 An air balloon is modelled as acting according to the following forces: i) Lift ii) Wind iii) Weight iv) Air resistance Model assumptions Model assumptions
Model assumptions An air balloon is modelled as acting according to the following forces: i) Lift ii) Wind iii) Weight iv) Air resistance i) The balloon is modelled as a particle (point) ii) The forces are constant iii) No other forces are involved
Force diagrams Intro 2 What will the air balloon do if these forces are i) Lift 200 N ii) Wind east 120 N iii) Weight 180 N iv) Air 70 N resistance RESULTANT force 50i + 20j Lift - Weight = 20 N upwards i is 1 unit along Wind - resistance = 50 N East j is 1 unit up The balloon is modelled as a particle
Force diagrams Intro 3 The balloonists throw out sandbags and the wind dies down RESULTANT force -20i + 35j i) Lift 200 N ii) Wind east 50 N iii) Weight 165 N iv) Air 70 N resistance Lift - Weight = 35 N upwards Wind - resistance = -20 N East
Force diagrams Intro 4 The balloonist reduces the flame and the wind changes direction i) Lift 110 N ii) Wind west 100 N iii) Weight 165 N iv) Air 70 N resistance Lift - Weight = -55 N downwards Wind - resistance = -30 N East -30i - 55j RESULTANT force
Force diagrams Intro 5 Split into components The balloon is being pushed by resultant force 120 N in a North east direction ?i + ?j Lift - Weight = ? Wind - resistance = ? 84.9i + 84.9j 120 450 120 sin45 = 84.9 120 cos45 = 84.9
WB1 Work out the Forces i i andj jcomponents: 11 cos 50 7 500 7 sin 60 -11 sin 50 11 600 7 cos 60 -8 cos 20 200 16 16 sin 40 -8 sin 20 8 1400 400 -16 cos 40
WB2 Work out the Forces i and j components for each step of the balloons journey: 450 22 300 36 600 33 25 750
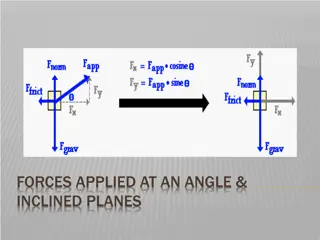
Force diagrams Intro 7 magnitude and direction What if we want the direction and magnitude of the resultant force i) ii) iii) Weight 180 N iv) Air 70 N resistance Lift 200 N Wind east 120 N 50i + 20j Lift - Weight = 20 N upwards Wind - resistance = 50 N East Magnitude = + = 2 2 50 20 53 9 . N 20 Direction = upwards from the horizontal 0 = 1 tan 21 8 . 20 50 50
WB3 Work out the direction and magnitude of each force: 0 = 1 tan 33 7 . 8 12 5i + 3j + = 2 2 12 8 14 42 . Direction 340 down from horizontal and magnitude 14.4 N 0 = 1 tan 31 3 5 + = 2 2 5 3 . 5 83 12i - 8j Direction 310 up from horizontal and magnitude 5.83 N 0 = 1 tan 60 3 . 7 4 + = 2 2 4 7 . 8 06 -4i - 7j Direction 1200down from horizontal and magnitude 8 N
Summary You should be able to: 1 add and subtract forces, finding resultant force 2 resolve forces into i and j components 3 resolve i and j components into magnitude and direction or vice versa F F sin A A F cos A To find the magnitude of a Force use Pythagoras To find the direction of a Force use Trigonometry (arctan (tan-1))
Plenary Discuss: In what context will we find Forces? What type of problems? engineering and building: strengths of materials holding up walls, floors, bridges sailing: forces = currents in the water and drive of the engine connected objects: car pulling a caravan; objects suspended by cables from cranes
Force Diagrams Hot air balloon Use trigonometry to find the components of a vector (or magnitude and direction) Find the resultant of two or more forces, as the sum of components self-assess One thing learned is One thing to improve is