Understanding ANOVA: Analyzing Variance in Medical Treatments
Explore how ANOVA (Analysis of Variance) can help in comparing multiple medical treatments by analyzing the days taken for patients to be cured. ANOVA checks if means of different groups are significantly different, providing a reliable method to make informed treatment decisions. Learn the basics, principles, and importance of ANOVA in evaluating treatment effectiveness.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
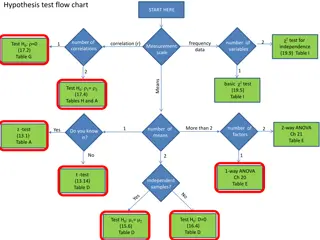
Introduction: Consider a scenario where we have three medical treatments to apply on patients with similar diseases. Once we have the test results, one approach is to assume that the treatment which took the least time to cure the patients is the best among them. What if some of these patients had already been partially cured, or if any other medication was already working on them? In order to make a confident and reliable decision, we will need evidence to support our approach. This is where the concept of ANOVA comes into play. A common approach to figure out a reliable treatment method would be to analyse the days it took the patients to be cured. We can use a statistical technique which can compare these three treatment samples and depict how different these samples are from one another. Such a technique, which compares the samples on the basis of their means, is called ANOVA. ANOVA (Analysis of Variance)
ANOVA Analysis of variance (ANOVA) is a statistical technique that is used to check if the means of two or more groups are significantly different from each other. ANOVA checks the impact of one or more factors by comparing the means of different samples. Another measure to compare the samples is called a t-test. When we have only two samples, t-test and ANOVA give the same results. However, using a t-test would not be reliable in cases where there are more than 2 samples.
ANOVA is essentially a procedure for testing the difference among different groups of data for homogeneity. The essence of ANOVA is that the total amount of variation in a set of data is broken down into two types, that amount which can be attributed to chance and that amount which can be attributed to specified causes. Thus, in general, through ANOVA technique one can, investigate any number of factors which are hypothesized or said to influence the dependent variable. One may as well investigate the differences amongst various categories within each of these factors which may have a large number of possible values. Through this technique one can explain whether various varieties of seeds or fertilizers or soils differ significantly so that a policy decision could be taken accordingly, concerning a particular variety in the context of agriculture researches. ANOVA
Basic Principles of ANOVA The basic principle of ANOVA is to test for differences among the means of the population examining the amount of variation within each of these samples, relative to the amount of variation between the samples. In terms of variation within the given population, it is assumed that the observation (x ) differ from the mean of this population only because of random effects i.e., there are influences on (x ) which are unexplainable, whereas in examining differences between populations we assume that the difference between the mean of the population and the grand mean is attributable to what is called a 'specific factor' or what is technically described as treatment effect. Thus, while using ANOVA, we assume that each of the samples is drawn from a normal population and that each of these populations has the same variance.
Basic Principles Cont.. The total variance in the joint sample is partitioned into two parts (i) between samples variance, and (ii) within samples variance. Between samples variance is due to different treatments, while within samples variance is due to the random unexplained disturbance. Using these two variances, we define the test statistic as: Fc = ??????? ?????? ???????? ??? ?? ?????? ???????? Using this method, we wish to test: H0 : All population means are the same ( or effects of all treatments are same) H1 : All population means are not the same (or effects of all treatments are not same)
ANOVA Methods If we take only one factor and investigate the differences amongst its various categories having numerous possible values, we are said to use one- way ANOVA. ANOVA ONE WAY ANOVA TWO WAY ANOVA In two-way ANOVA, the interaction or inter- relationship of two factors affecting the values of a variable can as well be studied for better decisions.
One Way ANOVA A one-way ANOVA uses one independent variable One-way ANOVA example : As a crop researcher, you want to test the effect of three different fertilizer mixtures on crop yield. You can use a one-way ANOVA to find out if there is a difference in crop yields between the three groups.
Two Way ANOVA A two-way ANOVA is used to estimate how the mean of a quantitative variable changes according to the levels of two categorical variables. We use a two-way ANOVA when we want to know how two independent variables, in combination, affect a dependent variable. Two-way ANOVA Example: You are researching which type of fertilizer and planting density produces the greatest crop yield in a field experiment. You assign different plots in a field to a combination of fertilizer type (1, 2, or 3) and planting density (1=low density, 2=high density), and measure the final crop yield in bushels per acre at harvest time. You can use a two-way ANOVA to find out if fertilizer type and planting density have an effect on average crop yield.
Difference between one-way and two-way ANOVA The only difference between one-way and two-way ANOVA is the number of independent variables. A one-way ANOVA has one independent variable, while a two-way ANOVA has two. One-way ANOVA: Testing the relationship between shoe brand (Nike, Adidas, Reebok, Puma) and race finish times in a marathon. Two-way ANOVA: Testing the relationship between shoe brand (Nike, Adidas, Reebok, Puma), runner age group (junior, senior, master s), and race finishing times in a marathon. All ANOVAs are designed to test for differences among three or more groups. If you are only testing for a difference between two groups, use a t-test instead.