Understanding ANOVA in Experimental Design
In this educational content, we delve into the key concepts of ANOVA (Analysis of Variance) in experimental design. Topics covered include the necessary assumptions for conducting one-way ANOVA, the importance of testing factors in two-way ANOVA, various types of sum of squares, comparisons between one-way and two-way ANOVA results, advantages of randomized block design, and terminology in ANOVA experiments. Additionally, we explore a real-world experiment determining the best cake baking combination for taste testing.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
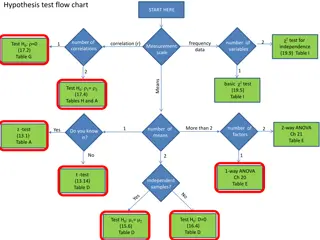
assumption 1-Which of the following is a necessary to conduct a one-way ANOVA comparing p population means? A -The p populations of values of the response variable associated with the treatments have equal variances. B-The p populations of values of the response variable associated with the treatments all have normal distributions.
C-The samples of experimental units associated with the treatments are randomly selected, independent samples. D-All of the above* 2-In two-way ANOVA, what should you always test first? A) The significance of factor1 B) The significance of factor 2 C-The interaction between factors 1 and 2* D) None of the above.
3-The ______ sum of squares measures the variability of the observed values of the response variable around their respective treatment means. A-treatment B-error* C-interaction D-total 4-The ________ sum of squares measures the variability of the sample treatment means around the overall mean A-treatment* B-error C-interaction D-total
5-Based on the results of a two-way ANOVA, the SSE was computed to be 139.42. If we ignore one of the factors and perform a one-way ANOVA using the same data, will the SSE be smaller than 139.42? A- Yes. Using the same data, the SSE based on a one-way ANOVA is always smaller than the SSE based on a two-way ANOVA. B- No. Using the same data, the SSE based on a one-way ANOVA is never smaller than the SSE based on a two-way ANOVA* C-Possibly. The SSE based on a one-way ANOVA could be smaller or larger than the SSE based on a two-way ANOVA.
6-The advantage of the randomized block design over the completely randomized design is that we are comparing the treatments by using ________________ experimental units A- randomly selected B-the same or similar* C- different D- representative 7-In a one-way ANOVA, different levels of the factor are called A-treatments* B-variables C-responses D-observations
8-Prior to introducing a new cake mix to the public, a food company wishes to determine the combination of baking temperature and baking time that will result in the best tasting cake. In their experiment, cakes made from the new cake mix are baked at 325 degrees F, 350 degrees F, and 400 degrees F for 50 minutes, 60 minutes, 70 minutes, and 80 minutes. Taste is rated for each combination of baking temperature and baking time. How many treatments are in the experiment A- 7 B-12* C-5 D-4 E-3
9-A consumer interest group wishes to compare the effectiveness of three competing brands of cough syrup. They take a random sample of 60 people with coughs and randomly assign 20 of these 60 people to each of the three brands of cough syrup. They then measure the decrease in cough frequency that each person experiences. This is an example of A-a completely randomized experimental design.* B-a randomized block experimental design.
10-Which of the following is NOT found in an ANOVA table for a randomized block design A-Sum of squares due to interaction* B- Sum of squares due to factor 1 C- Sum of squares due to factor 2 D- Total sum of squares
11-When conducting a one-way ANOVA, the ______ the between-treatment variability is when compared to the within-treatment variability, the ________ the value of F will be tend to be A- smaller, larger B-larger, smaller C- larger, larger * D- smaller, more random E-larger, more random
12-While conducting a one-way ANOVA comparing five treatments with 10 observations per treatment, you compute SSA = 42.41 and MSW = 6.34. What is the value of F? A- 42.41 B- 1.67* C- 6.34 D- 6.69 E- 0.74
13-While conducting a one-way ANOVA comparing five treatments with 10 observations per treatment, you compute SSA = 42.41 and MSW = 6.34. What are the degrees of freedom associated with F A) 5, 50 B) 5, 10 C) 4, 10 *D- 4,45
14-When comparing three treatments in a one-way ANOVA, the null hypothesis would be ; that is, all three treatments have the same effect on the mean response. In words, how would you interpret the alternative hypothesis Ha? A- At least two treatments are different from each other in terms of their effect on the mean response* B- All three treatments have different effects on the mean response C- Exactly two of the three treatments have the same effect on the mean response D- All of the above.
15 15- -The one The one- -way ANOVA is used to test statistical hypotheses way ANOVA is used to test statistical hypotheses concerning what? concerning what? Variances. Standard deviations. Squared means. Means*
16 16- -One way ANOVA, if the computed One way ANOVA, if the computed F F statistic exceeds the critical critical F F value, what decision can you make regarding the value, what decision can you make regarding the null hypothesis? null hypothesis? statistic exceeds the Reject H0 since there is evidence all the means differ. Reject Ho since there is evidence of a treatment effect.* Do not reject Ho since there is no evidence of a difference Do not reject Ho because a mistake has been made
17-What formula would you use to calculate the F test statistic for a one-way ANOVA experiment? A- MSW/MSA B- SSW/SSA C- MSA/MSW* D- SSA/SSW 18-How many degrees of freedom exist for the F test in a one-way ANOVA? A- (N-k) and (k 1) B-(k- 1) and (N k) C-(K-N) and (N- 1) D-(N- 1) and (K-N)