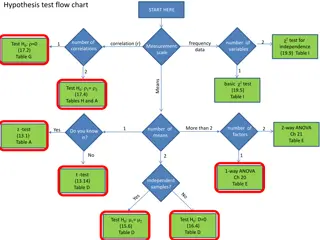
Analysis of Variance in Women's Professional Bowling Association - 2009

This study conducted a 2-Way Mixed Analysis of Variance on the Women's Professional Bowling Association qualifying rounds in 2009 at Alan Park, Michigan. The analysis focused on factors including oil pattern variations and different bowlers, each rolling sets of games on different patterns to measure total pins. The statistical model examined the effects of oil pattern, bowler, and their interaction, along with covariance structures and ANOVA analyses. Results encompassed population means, variance calculations, and expectations of means.

• Analysis of Variance
• Womens Bowling Association
• Sports Statistics
• Data Analysis

spola Follow

Uploaded on Sep 17, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. 2-Way Mixed Analysis of Variance Women s PBA - 2009

2. Data Description Women s Professional Bowling Association Qualifying rounds at Alan Park, Michigan (2009). Factors: A: Oil Pattern (Fixed) with a=4 levels: 1=Viper, 2=Chameleon, 3=Scorpion, 4=Shark B: Bowler (Random) with b=15 levels: 1=Diandra Abaty, 2=Shalin Zulkiffi, 3=Liz Johnson, 4=Kelly Kulick, 5=Clara Guerrero, 6=Jennifer Petrick, 7=Wendy MacPherson, 8=Shannon Pluhowski, 9=Stephanie Nation, 10=Tammy Boomershine, 11=Amanda Fagan, 12=Aumi Guerra, 13=Michelle Feldman, 14=Shannon O'Keefe, 15=Jodie Woessner Replicates: Each bowler rolled 2 sets of 7 games on each pattern (Y = Total Pins in a game, n=14)

3. Statistical Model ( ) = + + + + = = = = = = 1,..., 4; 1,..., 15; 1,..., 14 Y b ab e i a j b k n ijk i j ijk ij Overall Population mean across 4 oil patterns and population of bowlers ( ) ( Note that this is an Unrestricted Model (wrt interaction effect). 4 = th Effect of Oil Pattern: 0 i i i = 1 NID i ) 2 b th Effect of Bowler: ~ 0, b ( j b j j ( ) ( ) 2 ab th th Interaction Effect of Oil Pattern and Bowler: ~ 0, ab i j ab NID ij ij ) 2 Random Error term: ~ 0, e e NID ijk ijk ( ) b ab e j ijk ij Restricted Model (interaction effects sum to zero over oil patterns for all bowlers): ( ) ( ) ( ) ( ) ( ) ( ) * = + + + + + = + + + + * j Y b ab ab ab e b ab e ijk i j ijk i ijk j ij j ij ( ) 1 1 a a a ( ) ( ) ( ) ( ij ) * * * * = = 2 ab 2 ab 0 ~ 0, , ' ab ab N COV ab ab i i ' ij ij i j a = 1 i

4. Covariance Structure / ANOVA (Unrestricted Model) ' ' ' , ': COV , COV ijk i jk j i i k k Y Y b = + ' ' ' , ', , ':COV , COV ijk i jk j j i i k k Y Y = ijk E Y ( ( ) ) = + + + + = + 0 0 0 + + + = + E b ab e i j ijk i i ij = + + + + 0 0 = + + + + = + + 2 b 2 ab 2 2 b 2 ab 2 V Y V b ab e ijk i j ijk ij ) ( ( ) ( ) = + + + + = + 2 b 2 ab ': COV , COV , k k Y Y b ab e b ab e ' ' ijk ijk j ijk j ijk ij ij ( ) ( ( + + + = 2 b , ab e b ab e ' ' ijk j i jk ' ij i j ) ) + + + + = , 0 b ab e b ab ' ' ' i j k e ' j ijk j ' ' i j ij ( ) a a 2 2 i 2 = = SSA bn Y Y bn Y abnY i = = 1 1 i i ( ) b b 2 2 2 = = SSB an Y Y an Y abnY j j = = 1 1 j j ( ) a b a b a b 2 2 ij 2 i 2 2 = + = + SSAB n Y Y Y Y n Y bn Y an Y abnY ij i j j = = = = = = 1 1 1 1 1 1 i j i j i j ( ) a b n a b n a b 2 2 ij = = 2 SSE Y Y Y n Y ij ijk ijk = = = = = = = = 1 1 1 1 1 1 1 1 i j k i j k i j

5. Expectations and Variances of Means - I E Y E Y E Y ( ) E Y 2 = = + = + = = + 2 2 2 2 2 2 2 2 2 2 V Y E Y E Y Y V Y ijk E Y ijk E Y ijk V Y ( ) 2 = + = + + = + + + + 2 b 2 ab 2 2 2 b 2 ab 2 i i 1 n 1 n n ( ) = = + = + E Y E Y n ij ijk i i = 1 k + n 1 n 1 n 1 n n n ( ) ( ) ijk V Y = = + = + + + + = 2 b 2 ab 2 2 b 2 ab 2 COV , 2 V Y V Y Y Y n ij ' ijk ijk ijk 2 2 2 = = k k 1 1 ' k k + 2 b 2 ab 2 1 n 1 n n n ( ) ( ) ( ) 2 ij 2 = + + + + = + + = + + 2 b 2 ab 2 2 b 2 ab 2 2 b 2 2 ab 2 ( 1) n n n n n n E Y i 2 2 n = 1 b 1 b 1 n 1 n b n n ( ) = = + = + = Note: COV , C OV , 0 E Y E Y b Y Y Y Y ' i ij ij ij ' i i ijk ij k = = = 1 1 1 j k k 2 1 b 1 b 1 b b b = = + = + + + 2 b 2 ab 2 COV , ( 1)(0) V Y V Y V Y Y Y b b b ' i ij ij ij ij 2 2 n = = 1 1 ' j j j j + + + + 2 b 2 ab 2 2 b 2 ab 2 n n bn n n bn ( ) 2 i 2 = = + + E Y i

6. Expectations and Variances of Means - II 1 n 1 n 1 n n n = = = 2 2 b 2 b Note: COV , COV , Y Y Y Y n ' ij i j ' ijk i jk 2 = = 1 1 k k 1 a 1 a 1 a 1 a a a n ( ) = = + = + = + = 0 E Y E Y a j ij i i = = = 1 1 1 i i i 1 a 1 a b a = = + = 2 COV , V Y V Y V Y Y Y ' j ij ij ij i j 2 = = i i 1 1 ' j i + + 2 b 2 ab 2 2 1 a an n an = + + + = 2 b 2 2 b ( 1) a a a a b 2 n + + 2 b 2 ab 2 an n an 2 = + 2 E Y j 1 b 1 b b = = = E Y E Y b j = 1 j + + + + 2 b 2 ab 2 2 b 2 ab 2 1 b 1 b an n an an n b = = = V Y V Y b j 2 abn = 1 j + + 2 b 2 ab 2 an n 2 = + 2 E Y abn

7. Expected Mean Squares - I a 2 i 2 = SSA bn Y abnY = 1 i + + + + 2 b 2 ab 2 2 b 2 ab 2 n n bn an n a ( ) 2 = + + + 2 E SSA abn bn abn i abn = 1 i n n ( ) ( ) ( ) = an an + an n + + + + = 2 b 2 ab 2 2 2 i 2 1 2 a bn a abn i = = 1 1 i i n 2 i bn = n S a SA ( ) ( ) = + + = + + 2 2 ab 2 i 2 2 ab = 1 1 1 i a n a bn E MSA E n 1 1 a = 1 i b 2 2 = SSB an Y abnY j = 1 j + + + + 2 b 2 ab 2 2 b 2 ab 2 an n an an n = + + 2 2 E SSB abn abn abn ( ) ( ) ( ) = abn an + bn n + 2 b 2 ab 2 1 b SSB b ( ) ( ) ( ) = + + = = + + an 2 2 ab 2 b 2 2 ab 2 b 1 1 1 b n b an b E MSB E n 1

8. Expected Mean Squares - II a b a b 2 ij 2 i 2 2 = + SSAB n Y bn Y an Y abnY j = = = = 1 1 1 1 i j i j = E SSAB + + + + 2 b 2 ab 2 2 b 2 ab 2 n n n n bn n a ( ) ( ) 2 2 + + + + abn bn abn bn i i n = = 1 1 i i abn an abn + + + + + 2 b 2 ab 2 2 b 2 ab 2 an n an an n + + + 2 2 abn abn abn ( ) ( ) ( ) = + + abn an bn + + 2 b 2 ab 2 1 an n ab a b n n ( ) ( ) 2 2 + + + + 2 2 bn bn abn abn i i = = 1 + 1 i i ( ) ( ) ( )( ) ( )( ) = + n ab a b + = + 2 2 ab 2 2 ab 1 1 1 1 1 1 ab a b a b n a b SSAB = = + 2 2 ab E MSAB E n ( )( ) 1 1 a b

9. Expected Mean Squares III & F-Tests a b n a b 2 ij = 2 SSE Y n Y ijk = = = = = 1 1 1 1 1 i j k i j + + 2 b 2 ab 2 n n a a ( ) ( ) ( ) 2 2 = + + + + + + 2 b 2 ab 2 E SSE abn bn abn bn i i n = = 1 1 i i a a ( ) ( ) ( ) ( ) ( ) ( ) 2 2 = abn abn + abn abn + abn ab + + + = 2 b 2 ab 2 2 1 bn bn ab n i i = = 1 1 i i = SSE = 2 E MSE E ( ) 1 ab n MSAB MSE H 0 = = 2 ab 2 ab : 0 : 0 : ~ H H TS F F ( )( ) ( ) 1 , 0 A AB 1 1 a b ab n MSB MSAB H 0 = = 2 b 2 b : 0 : 0 : ~ H H TS F F ( ) ( )( ) 1 , 0 A B 1 1 b a b MSA MSAB H 0 = = = = : 0 : Not all 0 : ~ H H TS F F ( ) ( )( ) 1 , 0 1 a A i A 1 1 a a b

10. Bowling Results (a=4, b=15, n=14) Mean Bowler1 Bowler2 Bowler3 Bowler4 Bowler5 Bowler6 Bowler7 Bowler8 Bowler9 Bowler10 Bowler11 Bowler12 Bowler13 Bowler14 Bowler15 Mean OilPatt1 OilPatt2 OilPatt3 OilPatt4 Mean SD 223.29 208.79 195.57 211.79 195.71 196.43 218.14 208.50 209.64 219.43 216.64 212.43 210.57 198.43 204.71 211.00 203.29 193.07 223.36 199.29 194.43 209.57 214.21 208.64 199.57 198.57 193.29 205.86 213.71 198.36 202.50 205.29 194.36 206.21 182.64 196.14 198.50 207.86 210.71 212.00 205.86 208.29 199.57 209.79 204.86 210.09 204.57 201.40 OilPatt1 OilPatt2 OilPatt3 OilPatt4 42.44 22.98 28.77 27.06 24.51 26.23 18.72 21.74 20.77 18.80 30.91 16.90 34.26 30.29 25.17 31.64 27.98 21.67 33.02 20.73 26.88 14.49 31.98 25.80 15.51 22.39 30.03 25.49 27.98 23.93 211.00 209.66 Bowler1 191.57 198.88 Bowler2 215.50 212.95 Bowler3 216.21 216.18 Bowler4 219.07 208.20 Bowler5 187.14 198.63 Bowler6 221.07 209.54 Bowler7 201.29 208.43 Bowler8 204.43 198.96 Bowler9 219.29 209.30 Bowler10 207.57 202.43 Bowler11 194.00 194.75 Bowler12 193.86 202.73 Bowler13 220.21 211.59 Bowler14 208.64 205.71 Bowler15 207.39 205.86 27.27 24.31 27.78 27.52 28.70 23.72 20.24 20.76 18.57 31.23 21.40 16.73 25.88 22.43 20.27 28.85 19.77 14.09 35.62 24.82 30.82 22.84 25.94 26.78 27.84 17.67 26.59 33.64 13.01 13.62 ANOVA Source Oil Pattern Bowler OilPattxBowler Error Total df SS MS MSError F* F(0.05) P-value 0.0217 0.0082 0.1271 3 8785.1 29964.7 34423.2 2928.4 2140.3 819.6 649.6 819.6 819.6 649.6 3.573 2.611 1.262 2.827 1.935 1.400 14 42 780 506679.0 839 579852.0

11. Estimating Population Mean Score = E Y + + 2 b 2 ab 2 an n = V Y abn n + = + 2 b MSB abn 2 ab 2 E MSB an ^ = V Y MSB abn ( ) 1 100% CI for : Y t /2, 1 b Bowling Data: = = = = = = 205.9 2.145 2140.3 4 15 14 Y .025,14 t MSB a b n 2140.3 4(15)(14) 2140.3 840 MSB abn = = = = 2.55 1 .60 MSB abn ( ) 205.9 2.145(1.60) 205.9 3.43 (202.47,209.33) 1 100% CI for : Y t /2, 1 b

12. Simple Effects Comparing Oil Patterns Within Bowlers Differences in pattern means for a given bowler: Estimator: Y Y ' ij i j 2 1 n = + + = + + = 2 2 b 2 2 ab 2 2 b 2 ab V Y n n n V Y ' ij i j 2 n 1 n 1 n 1 n n n = = = 2 2 b 2 b COV , COV , Y Y Y Y n ' ij i j ' ijk i jk 2 = = 1 1 k k ( ) + 2 2 ab 2 n 2 V Y = + = + + = 2 b 2 ab 2 b 2COV , 2 2 V Y Y V Y Y Y ' ' ' ij i j ij i j ij i j n n 2 MSAB n ^ = + = 2 2 ab E MSAB n V Y Y ' ij i j ( ) 2 MSAB n ( ) 1 100% CI for Simple Effect: Y Y t ' ij i j 1)( /2,( 1) a b 2 2(819.6) 14 MSAB n = = For Bowling Data: =2.018 10.82 .025,42 t 2 MSAB n = = 2.018(10.82) 21.83 t 1)( /2,( 1) a b

13. Marginal Effects Comparing Oil Patterns Across Bowlers Differences in pattern means across bowlers: + + = Estimator: Y Y ' i i 2 b 2 ab 2 n n bn = V Y V Y ' i i ( ) ( ) 1 b 1 b 1 b b b b = = + = COV , COV , COV , 2 COV , Y Y Y Y Y Y Y Y ' ' ' ' ' i j i i ij i j ij i j ij 2 = = = j j 1 1 1 ' j j j 2 b 1 b b b ( ) + = 2 b 1 0 b 2 b ( ) + 2 ab bn 2 2 n + + 2 b 2 ab 2 2 b n n bn = + = = 2COV , 2 2 V Y Y V Y V Y Y Y ' ' ' i i i i i i b 2 MSAB bn ^ = + = 2 ab 2 E MSAB n V Y Y ' i i ( ) 2 MSAB bn ( ) 1 100% CI for Marginal Effect: Y Y t ' i i 1)( /2,( 1) a b 2 2(819.6) 15 14 2 MSAB bn MSAB bn = = = = For Bo wling Data: =2.018 2.80 2.018(2.80) 5.65 .025,42 t t 1)( /2,( 1) a b

14. Pairwise Comparisons Among Oil Patterns Family: All Comparisons among Oil Patterns (Within Bowler and Across Bowlers) = 4 Oil Patterns = 15 Bowlers = 14 Replicates # of Oil Patterns = 4, # Pairs of Oil Patte = 819.6 ) = ( -1)( -1) = 42 df MSAB a b n MSAB ( rns = 4(3)/2 = 6 a b 2 2 MSAB n MSAB bn = = = = 10.82 2.80 SE Y Y SE Y Y ' ' ij i j i i ( ) ( ) = = Critical Values: Tukey: .05,4,42 3.784 Bonferroni: .025/6,42 2.764 q t Oil Pattern Scorpion Chameleon Shark Viper i Marginal 201.40 204.57 207.39 210.09 Comparing Simple (Within Bowler) 3.784 Tukey: 10.82 = 28.95 Bonferroni: 2.764(10.82) = 29.91 2 Means: 3 2 4 1 ( ) Comparing Marginal (Across Bowler) Means: 3.784 Tukey: 2.80 = 7.49 Bonferroni: 2.764(2.80) = 7.74 2 ( ) Oil Pattern Scorpion Chameleon Shark Viper i Bowler 1 195.57 208.79 211.00 223.29 3 2 4 1

15. Estimating Variance Components ~ = = 2 2 E MSE MSE ~ MSAB MSE = + = 2 2 ab 2 ab E MSAB n n ~ MSB MSAB an = + + = 2 2 ab 2 b 2 b E MSB n an = = = = = 649.6 819.6 2140.3 14 4 MSE MSAB MSB n a ~ ~ = = = 2 649.6 25.5 MSE ~ 819.6 649.6 14 170.0 14 MSAB MSE ~ = = = = = 2 ab 12.14 3.5 ab n ~ 2140.3 819.6 4(14) 1320.7 56 MSB MS an AB ~ = = = = = 2 b 23.58 4.9 b

16. Output from SAS PROC MIXED data wpba2009; infile 'wpba2009.dat'; input bowler 7-8 pattern 16 set 24 game 32 score 38-40; run; proc mixed covtest cl; class bowler pattern; model score = pattern; random bowler bowler*pattern; run; quit; The Mixed Procedure Covariance Parameter Estimates Standard Z Cov Parm Estimate Error Value Pr > Z Alpha Lower Upper bowler 23.5846 14.7947 1.59 0.0555 0.05 9.2431 138.95 bowler*pattern 12.1437 12.9894 0.93 0.1749 0.05 3.1052 757.62 Residual 649.59 32.8932 19.75 <.0001 0.05 589.65 719.20 Type 3 Tests of Fixed Effects Num Den Effect DF DF F Value Pr > F pattern 3 42 3.57 0.0217