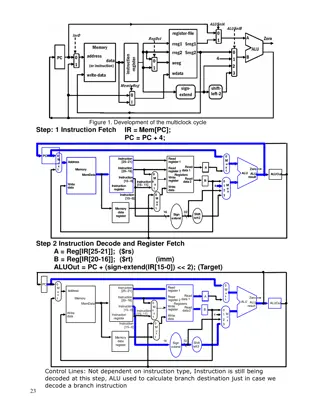
Trapping Modelling in MatCalc: Understanding Gibbs Energy and Configurational Entropy
Trapping modelling in MatCalc involves studying the entrapment of atoms on lattice defects like solute atoms and dislocations. This process affects the system's energy and concentration, with parameters such as trapping enthalpy, nominal composition, and molar volume playing vital roles. By considering state variables, constraints, thermodynamics principles, and Gibbs energy derivation, researchers can better comprehend the impact of trapping phenomena in materials science.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Trapping Modelling in MatCalc Yao V Shan
Introduction Trapping: atoms sticking to lattice defects (e.g. solute atoms, dislocations, grain boundaries, ) Cottrell atmosphere seen as trapping of carbon atoms along dislocations Pereloma et al. 2007
Given parameters Trapping enthalpy E: reduction of system energy per trapped atom Nominal composition of trapped element ci Amount of trapping positions cdef (solute atoms: nominal composition of trapping element, dislocations: dislocation density) Molar volume Temperature T
State variables Concentration of free atoms (in lattice) and trapped atoms: cL cT Volumes corresponding one mole of lattice positions and trap positions: VL VT Site fractions in lattice positions and trap positions: yL yT
Trapping On solutes: On dislocations:
Constraints Mass balance c = + c c i L T Molar volume 1 = 1 1 + V V L T Defects generate the molar trapping volume 1 = V T Zc def Site fractions y = y = c V c V T T T L L L
Thermodynamics Gibbs energy: = G H TS 0 Effect of trapping H G = TS c E 0 c T configurational entropy moles of trapped atoms trapping enthalpy Sc cT E
Configurational entropy Bragg-Williams approximation ln Sc y y Dividing the lattice into free and trapped portions: ln / T T y V ) + + / ln 1 ( ) ln( 1 ) V y y y y L L L L L = S R c g + 1 ( ) ln( 1 y y y T T T /VL fraction of lattice sites /VT fraction of trap sites
Gibbs energy Gibbs energy + + / ln 1 ( ) ln( 1 ) V y y y y L L L L L = + G H R T y E 0 g T + / ln 1 ( ) ln( 1 ) V y y y y V T T T T T T Equilibrium L y G = 0 Applying constraints = y = = ( V ) ( V ) L y c V c c c T T T i L T i T V Partial derivative y = L V T T y V L L
Gibbs energy derivation Derivation + + V V + / ln 1 ln( y 1 ) 1 V y y V dG V L L L = + = 0 T R T E g + / / ln / / ln( 1 ) / V V V V V y V V dy V T T L T T L T L T T L L T L Simplifying to V y 1 ( ) dG y y = + = ln 0 L T R T E g 1 ( ) dy y L L L T Equilibrium equation R y 1 ( ) y y E = exp L T Oriani 1970 1 ( ) y T L T g
Exact analytical solution Knowing y = ( V ) L y c T i T V L and 1 ( ) y y E = = exp L T K 1 ( ) y y R T L T g One can find yLat equilibrium + + + + 2 ( ) ( 4 )( ) KV c V V c V V K V KV c V V c V V K V V KV c V V K = T i L T i L T L T i L T i L T T T i L T y L ( 2 ) V KV T T
Real system Carbon on dislocations Trapping enthalpy: 75000 = 20 E T (Clouet et al. 2008) Coordination number Z for dislocations: 1 ~T Z (Cochardt et al. 1955) 2 Around 15 C atoms on a screw dislocation plane at room temperature (edge dislocation about half as much): (Cochardt et al. 1955) A = , 100000 Z A 2 T
Effect of trapping Cementite fraction over temperature Dislocation density Increasing dislocation density dissolves cementite at lower temperatures
Expansion to multi elements Multi trapping: e.g. carbon and nitrogen Gibbs energy = + / G H 0 + + + ln ln 1 ( ) ln( 1 ) V y y y y y y y y , , , , , , , , L L C L C L N L N L C L N L C L N R T g + + / ln ln 1 ( ) ln( 1 ) V y y y y y y y y , , , , , , , , T T C T C T N T N T C T N T C T N y E y E , , T C C T N N V V T T Equlibrium dG/dyL,C = 0 and dG/dyL,N = 0 leads to 1 ( ) y y y E , , , L C T C T N C = exp McLean 1957 1 ( ) y y y R T , , , L C L N T C g 1 ( ) y y y E , , , L N T C T N N = exp 1 ( ) y y y R T , , , L C L N T N g
Expansion to multi traps Gibbs energy + = H G 0 i i i + + / ln 1 ( ) ln( 1 ) V y y y y L Li Li Li Li k R T y E g Tki ki V i i i Tk i + / ln 1 ( ) ln( 1 ) V y y y y Tk Tki Tki Tki Tki k Equlibrium equations (i k equations) i 1 ( ) y l= 1, 2, , k Tki y E Lj lj k i = exp j= 1, 2, , i y R T 1 ( ) y Tlj g Li
Kinetics Kinetics are obtained from the balance equation for the Gibbs energy (thermodynamic extremal principle1): Q G = Total dissipation at dislocations in system due to carbon diffusion 4 y V y D T L R Ta V 3 R g L 2 ln Q T 2 4 a V a acting radius of dislocation R radius surrounding dislocation in a unit cell dislocation density D Diffusion coefficient of carbon a = T = R 1Svoboda et al. 2006
Kinetics At dislocations: ( ( ) ) R 2 1 D y y E = + ln L T y y T L 1 y y T 3 R 2 T L g ln a 4 a At grain boundaries: ( ( ) ) R 10 1 D y y E = + ln L T y y T L 1 R y y T G T L g R grain radius in a unit cell grain boundary thickness
Parameter study = f V T * = x y T = x c carbon 2 D = t 2 (ln( / ) 3 / ) 4 a R a Cottrell theory in dashed lines: * 2 / 3 x t
Summary Thermodynamic model for describing various trapping effects Derivations of the presented model lead to known equations, which has been used in empirical models for equilibrium Expansion of model for multi components Kinetic equations for slow non- equilibrium processes
More fun Chemical potentials y y = + ln L y R T 0 L g Ruda et al. 2009 1 L = + ln T R T E 0 T g 1 y T Extracting E from CALPHAD data by comparing chemical potentials Svoboda et al. 2011
More fun Diffusion coefficients ~ c = = j D c ( j ) div t + 4 1 ( V ) / D cV K V V K ~ D = + 1 L L T 2 + 2 1 ( L ) / ) 1 ( ) cV K V K cV K K L T L Trapping reduces the effective diffusion coefficient Svoboda et al. 2011
