System Analysis Exercises and Solutions
Explore a series of exercises and solutions on system analysis, including finding transfer functions, damping ratios, settling times, stability analysis, error constants, and more for different types of systems. Dive into each exercise to enhance your understanding of control systems.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
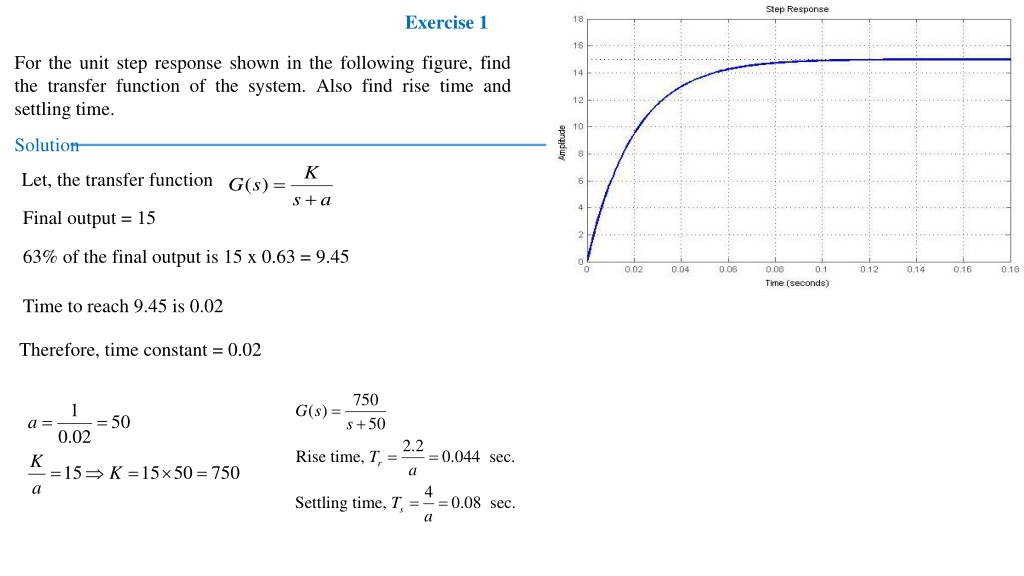
Exercise 1 For the unit step response shown in the following figure, find the transfer function of the system. Also find rise time and settling time. Solution K + Let, the transfer function = ( ) G s s a Final output = 15 63% of the final output is 15 x 0.63 = 9.45 Time to reach 9.45 is 0.02 Therefore, time constant = 0.02 750 s + = 1 ( ) G s = = 50 a 50 0.02 2.2 a = = Rise time, 0.044 sec. T K a r = = 15 50 = 15 750 K 4 a = = Settling time, 0.08 sec. T s
Exercise 2 ? ? ? = Find the ramp response for a system whose transfer function is: Solution ? + 2 ? + 3 1 ?2, Ramp input ? ? = 1 ?2 ? 1 we have ? ? =? ? ?(?) The output? ? = ?(?)? ? ? ? = = ? + 2 ? + 3 ? ? + 2 ? + 3 ? ? =? ? ? ?+ + ? + 2 ? + 3 Using partial fraction: 1 = 16 ? = ? + 2 ? + 3 ?=0 16 ? 13 ? + 3 12 ? + 2 1 12 ? ? = + ? = = ? ? + 3 ?= 2 1 = 13 ? = ? ? + 2 ?= 3 ? ? =1 6 1 2? 2?+1 The inverse Laplace Transform: 3? 3?
Exercise 3 For the unity feedback system with a unit step input, find: 1. Closed-loop transfer function. 2. Damping ratio, the natural frequency and the expected percent overshoot. 3. The settling time. Solution 1. Closed-loop transfer function 2 ?? The expected percent overshoot ??? ?????? ????? ?????? ????????? ???? ? ? = 2 ?2+ 2???? + ?? 3 The settling time
Exercise 4 For the characteristic equations below, Find the range of gain K, that will cause the system to be stable, unstable, and marginally stable. 1. ?4+ 6?3+ 11?2+ 6? + ? = 0 2. ?3+ 2 ?2+ 4 ? + ? = 0 Solution System1: ?4+ 6?3+ 11?2+ 6? + ? = 0 The system is stable for 60 6? > 0 ? < 10 The system is unstable for ? > 10 The system is marginally stable for ? = 10 ??? 10?2+ 10 = 0 ?1,2= ? System2:?3+ 2 ?2+ 4 ? + ? = 0 The system is stable for 0 < ? < 8 The system is unstable for ? > 8 The system is marginally stable for ? = 8 ??? 2?2+ 8 = 0 ?1,2= ?2
Exercise 5 Given the following non-unity feedback system, find the following: Evaluate the static error constants and find the expected error for the standard step, ramp, and parabolic inputs. Solution expected Steady state error the static error constants 1 For step input: ? = ) ??= lim ?(? = 1+??= 0 ? 0 1 ??= 0.2 For ramp input: ? = 50 1 2 5= 5 ??= lim ? 0? ? ? = 1 ??= For parabolic input: ? = ?2?(? = 0 ) ??= lim ? 0
Exercise 6 For the unity feedback system shown below, find: a) The static error constants ??,??,?? b) The steady-state error for an input of ?(?). c) The steady-state error for an input of 2 ? ?(?). d) The steady-state error for an input of 3 ?2 ?(?). Solution ? 0?2?(?) = 0 a) ??= lim ??= lim ??= lim ? 0?(?) = , ? 0?? ? = 66.7 , 1 b) for ? ? = ? ? ? = 1+??= 0 2 c) for ? ? = 2 ? ? ? ? = ??= 0.03 6 d) for ? ? = 3 ?2 ? ? ? = ??=