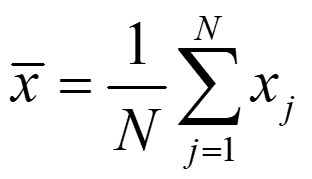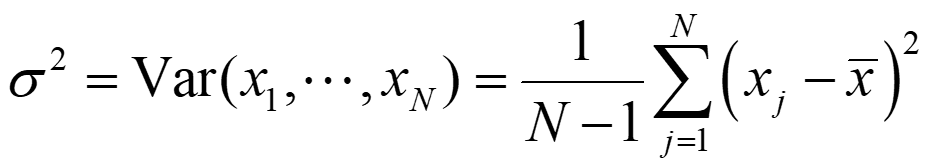Statistical Modeling and Analysis
Exploring statistical concepts such as mean, variance, skewness, kurtosis, Gaussian distribution, least squares fitting, chi-square fitting, and goodness-of-fit in data analysis. Learn about fitting parameters, probability computation, and interpretation of model goodness.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Chapter 15 Modeling of Data
Statistics of Data N 1 N = Mean (or average): x x j = 1 j N 1 ( ) 2 Variance: = = 2 Var( , , ) x x x x 1 N j 1 N = 1 j Median: a value xjsuch that half of the data are bigger than it, and half of data smaller than it. is called standard deviation. Error estimate ? ?/ ?
Higher Moments 3 x x N 1 N j = Skew( , , ) x x 1 N = 1 j 4 x x N 1 N j = Kurt( , , ) 3 x x 1 N = 1 j
Gaussian Distribution 2 ( ) x a 1 = 2 ( ; , ) N x a e 2 2 = x a = = = 2 Var( ) Skew( ) Kurt( ) x 0 x 0 x
Least Squares Given N data points (xi,yi), i = 1, , N, find the fitting parameters aj, j = 1, 2, , M of a function f(x) = y(x; a1,a2, ,aM) such that 1 1 i = N 2 ( ; , i y x a , ) y a i M is minimized over the parameters aj.
Why Least Squares Given the parameters, what is the probability that the observed data occurred? Assuming independent, Gaussian distribution, that is: 2 N ( ) y x 1 2 y exp i i P y i = 1 i i
Chi-Square Fitting Minimize the quantity: 2 ( ; , i y x a , ) y a N 2 1 i M = 1 i i If each term is an independent Gaussian, 2 follows so-called 2 distribution. Given the value 2 above, we can compute Q = Prob(random variable chi2 > 2) If Q < 0.001 or Q > .999, the model may be rejected.
Meaning of Goodness-of-Fit Q ( ) If the statistic 2 indeed follows this distribution, the probability that chi- square value is the currently computed value 2, or greater, equals the hashed area Q. 2 2 2 ( ) exp /2 P Observed value of 2 It is quite unlikely if Q is very small or very close to 1. If so, we reject the model. Area = Q Number of degrees of freedom = N M. 0 2
Fitting to Straight Line (with known error bars) Given (xi, yi i) Find interception a and slope b such that = y 2 y a bx N 2 ( , ) a b i i = 1 i i the chi-square merit function is minimized. Goodness-of-fit is Q=gammq((N-2)/2, 2/2). If Q > 0.1, the fitting is good, if Q 0.001, may be OK, but if Q < 0.001, fitting is questionable. fitting to y=a+bx If Q > 0.999, fitting is too good to be true. x
Linear Regression Model Error in y, but no error in x. y Data do not follow exactly the straight line. The basic assumption in linear regression (least squares fit) is that the deviations are independent gaussian random noise. fitting to y=a+bx x
Solution of Straight Line Fit = = 2 2 0, 0 a b x y 1, N N N , i i S S S x y 2 i x = 2 i 2 i = = = 1 1 1 i i i 2 i x y N N , i i S S xx xy 2 i 2 i = = 1 1 i i + aS bS S x y S + = 2 x S S , aS bS SS S x xx xy xx S S S S SS xx y x xy xy x y = = , a b
Error Propagation Let z = f(y1,y2, ,yN) be a function of independent random variables yi. Assuming the variances are small, we have ( i i i y y N f = ) z z y y i = 1 i Variance of z is related to variances of yi by 2 2 f i i i y = 2 N f = 1
Error Estimates on a and b Using error propagation formula, viewing a as a function of yi, we have S S x a y = = xx x i 2 i i Thus 2 S S x S N = 2 a 2 i xx x i xx 2 i = 1 i S Similarly = 2 b
What if error in yi is unknown? The goodness-of-fit Q can no longer be computed Assuming all data have same : 1 i = N 2 = 2 M is number of basis functions, M=2 for straight line fit. ( ) /( i y x ) y N M i Error in a and b can still be estimated, using i= (but less reliably)
General Linear Least-Squares Fit to a linear combination of arbitrary functions: M y x a X x = = ( ) ( ) k k 1 k E.g., polynomial fit Xk(x)=xk-1, or harmonic series Xk(x)=sin(kx), etc The basis functions Xk(x) can be nonlinear
Merit Function & Design Matrix Find ak that minimize 2 M ( ) x y a X N i k k i = 2 = 1 k = 1 i i a a 1 Define Let a be a column vector: 2 = a ( ), X x y j i = = i A b ij i a i i M The problem can be stated as 2 2 Min || || b Aa
Normal Equation & Covariance The solution to min ||b-Aa||2 is ATAa=ATb Let C = (ATA)-1, then a = CATb We can view data yi as a random variable due to random error, yi=y(x)+ i. < i>=0, < i j>= i2 ij. Thus a is also a random variable. Covariance of a is precisely C <aaT>-<a><aT> = C Estimate of the fitting coefficientis T j jj j CA b = a C
Singular Value Decomposition We can factor arbitrary complex matrix as A = U V a a a U U U 0 0 w 11 1 11 1 M N 1 * * V V V 11 * 12 1 M 0 N M 21 21 = M M N M N N 0 0 w M * V MM a a U 0 0 1 N NM NN U and V are unitary, i.e., UU =1, VV =1 is diagonal (but need not square), real and positive, wj 0.
Solve Least-Squares by SVD From normal equation, we have = 1 T T ( ) a A A A b = = T T T ( ( ) ) AB AB B A B A 1 1 1 A U V = T but ( ( V ) 1 = U V U V U V T T T T T so ( ) ( ) a b ) ( ) 1 1 = = T T T T T T T T T V U U V V U b V V V U b = = 1 1 T T T T T T T ( ) ( ) V V U b V U b T U b Omitting terms with very small w gives robust method. ( ) j w = a V Or ( ) j = , 1, , w j M j j
Nonlinear Models y=y(x; a) 2 is a nonlinear function of a. Close to minimum, we have (Taylor expansion) 1 2 ( ) = + + 2 3 T ( ) a a a a D a a a a ( ) ( ) ( ) ( ) O min min min min 1 2 + a T T d a D a where 2 2 ( ) a = 2 d D a ( ), a + = D ij a a i j
Solution Methods Know gradient only, Steepest descent: = 2 a a a constant ( ) next cur cur Know both gradient and Hessian matrix: = 1 2 a a D a ( ) min cur cur Define a a ( ; ) i y x a ( ; ) i y x a 1 2 1 N = = 2 , kl 2 i = 1 i k l
Levenberg-Marquardt Method Smoothly interpolate between the two methods by a control parameter . =0, use more precise Hessian; very large, use steepest descent. Define new matrix A' with elements: + = (1 ), if if i i j j ii ij , ij
Levenberg-Marquardt Algorithm Start with an initial guess of a Compute 2(a) Pick a modest value for , say =0.001 ( ) Solve A' a= , evaluate 2(a+ a) If 2 increase, increase by a factor of 10 and go back to ( ) If 2 decrease, decrease by a factor of 10, update a a+ a, and go back to ( )
Problem Set 9 (3 Nov) 1. If we apply the Levenberg-Marquardt method for a linear least-square problem, what are A and ? How many iterations are needed for convergence with a judicious choice of starting condition? 2. Radiative decay data can be fitted to the sum of two exponentials, ?1? ?/?1+ ?2? ?/?2. Apply the Levenberg-Marquardt method for nonlinear least-squares fit implemented in scipy optimize.curve_fit(f, x, y, , method= lm ). Use the data file nfit.dat posted, to determine the fitting parameters.