Radiative Transfer in Saturn's Moon Enceladus
Exploring the detection and characterization of water vapor, ice particles, and liquid water on Saturn's moon Enceladus using radiative transfer techniques at specific wavelength ranges. The study involves analyzing a thermal map of fractures on the moon and explains the use of wavelengths between 12 and 16 micrometres. Various images and equations illustrate the principles of multiple scattering and energy conservation in the atmosphere of Enceladus.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
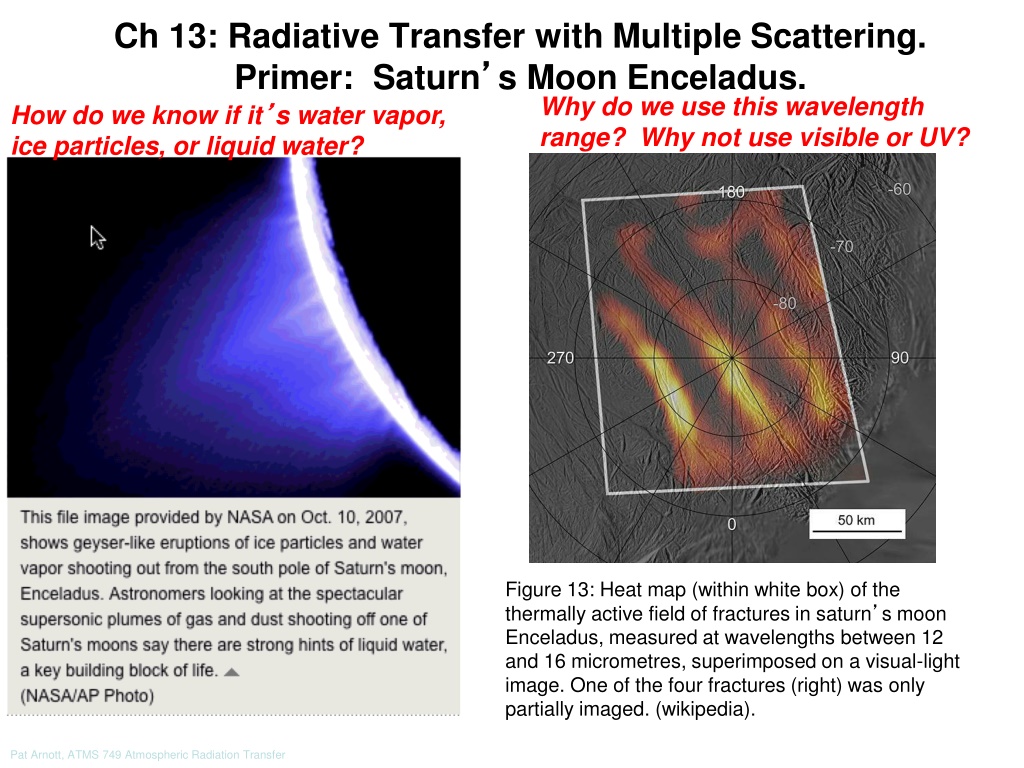
Ch 13: Radiative Transfer with Multiple Scattering. Primer: Saturn s Moon Enceladus. How do we know if it s water vapor, ice particles, or liquid water? Why do we use this wavelength range? Why not use visible or UV? Figure 13: Heat map (within white box) of the thermally active field of fractures in saturn s moon Enceladus, measured at wavelengths between 12 and 16 micrometres, superimposed on a visual-light image. One of the four fractures (right) was only partially imaged. (wikipedia). Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Two Stream Approximation: Multiple Scattering in 1 dimension. 0, top of atmosphere I (z) I (z) z arbitrary layer dz extdz = absdz + scadz. P = P . P = P . z + dz I (z+dz) I (z+dz) h, ground level extdz = Probability a photon undergoes extinction in dz. absdz = Probability a photon is absorbed in dz. scadz = Probability a photon is scattering in dz. P = P = Probability a downward photon is scattered up, and vica versa. P = P = Probability an upward photon is scattered up, and vica versa. P + P = 1 all of the choices for a scattered photon in 1 dimension. Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Conservation of energy in dz for downward intensity (or flux): (seeking relationships between the fluxes above and below dz). 0, top of atmosphere I (z) I (z) z arbitrary layer dz extdz = absdz + scadz. P = P . P = P . z + dz I (z+dz) I (z+dz) h, ground level Gain of downward flux by layer dz = Loss of downward flux by layer dz. (No flux is generated in the layer by emission. Easy to do emission later.) I (z)+ sca P dz I (z+dz) = absdz I (z) + sca P dz I (z) + I (z+dz) absorption scattering transmission Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Conservation of energy in dz for upward intensity (or flux): (seeking relationships between the fluxes above and below dz). 0, top of atmosphere I (z) I (z) z arbitrary layer dz extdz = absdz + scadz. P = P . P = P . z + dz I (z+dz) I (z+dz) h, ground level Gain of upward flux by layer dz = Loss of upward flux by layer dz. (No flux is generated in the layer by emission. Easy to do emission later.) I (z+dz)+ sca P dz I (z) = absdz I (z+dz) + sca P dz I (z+dz) + I (z) absorption scattering transmission Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Form Differential Equations from the Difference Equations Derived 0, top of atmosphere I (z) I (z) z arbitrary layer dz extdz = absdz + scadz. P = P . P = P . z + dz I (z+dz) I (z+dz) h, ground level Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Aside: Asymmetry Parameter of Scattering, g. -1<g<1 nr=1.33 =0.6328 D=20 um g=0.874 Is( ) I0 Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Scattering Relationships: Example and the Asymmetry Parameter g Here P =3/4. P =1/4. P + P = 1. incoming photons back scattered photon g P - P in 1-D. g = P - (1- P ) particle Solving, P =(1+g)/2 = P forward scattered photons P =(1-g)/2 = P Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Relationships for Extinction, Scattering, Absorption, and the Single Scatter Albedo: Coupled de s for the fluxes. Fundamental equations we use for everything. Fluxes are coupled by scattering. Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Special Case: No Absorption, Single Scatter Albedo = 1. Reflection and Transmission Coefficients, R and T. R I (0)/ I0 I (0) I0 0, top of atmosphere = T I ( ) / I0 h, ground level = ground is a totally absorbing surface, I ( = ) 0. Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Solving for the Case where Single Scattering Albedo=1 (no absorption) Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Features of the Solution for R and T with no Absorption g and are not uniquely determined by R and T measurements,only the product ( (1-g) is uniquely determined. g=1, forward scattering only, then R=0, T=1. g=-1, R 1 because of multiple scattering, R= ( + ) = ( + ) However, dilute milk will be colored blue (Rayleigh scattering) Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Features of the Multiple Scattering Solution Continued ... 1 R T Photons are lost to the downward stream only if they are scattered in the opposite direction Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Direct and Diffuse Transmitted Radiation Diffuse = Total - Direct Cloud optical depth I0 Ir cloud H LWP = Cloud Water Mass / Area Qext = Cloud droplet extinction efficiency CCN = # cloud condensation nuclei It nr=1.33 =0.6328 D=20 um g=0.874 figure 1 Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Can show that the downwelling diffuse radiation in the single scattering limit is matches expectations from direct integration of the radiative transfer equation in the single scattering approximation (done in class for Rayleigh scattering). Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Summary of Multiple Scattering Equations: 1 D model. Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
R and T: Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Reminder from Chapter 7 Presentation Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Optical Depth from kext: Liquid Water Path ztop Liquid Water Path zbot Somewhere there has to be an integral over z! Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Homework Problem: Aerosol Indirect Effect Reproduce the figure on the next slide using the simple model with absorption for the values of = 1 and 1. Calculate the cloud albedo as a function of effective radius and liquid water path for single scattering albedo equal to 1.0, and 0.95. In the second problem, assume that the absorption is caused by black carbon aerosol embedded in the cloud. Calculate the absorption coefficient necessary to give the value of the single scattering albedo as a function of the liquid water path. Comment on the likelihood of observing these absorption coefficients. Finally, comment on how aerosol light absorption impacts the aerosol indirect effect (i.e. the increased cloud albedo because of smaller more numerous droplets). Note: the mean free path of photons between scattering events is = 1 / sca. Tdir = exp(- exth)= exp(- ) = probability that photons pass through the general medium without interaction with the scatterers and absorbers. (Ballistic, unscattered photons useful for imaging in scattering medium with fast lasers that can gate out scattered photons that arrive later due to their larger path length). Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Cloud Liquid Water Path, Effective Radius, And Cloud Albedo Does this make sense? Why? How do things change when the single scattering albedo is not equal to 1, and absorption happens? grams / m2 Global Survey of the Relationships of Cloud Albedo and Liquid Water Path with Droplet Size Using ISCCP.Preview By: Qingyuan Han; Rossow, William B.; Chou, Joyce; Welch, Ronald M.. Journal of Climate, 7/1/98, Vol. 11 Issue 7, p1516. Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Cloud above a Reflecting Ground I (0) 1 R T2Ag T2AgRAg T2Ag(RAg)2 T2Ag(RAg)n TAgRAgRAg TAg TAgRAg T(AgR)n TAg (AgR)n TAgR T TAgRAgR ground has reflectance, (or albedo) = Ag. Rtotal= R+T2Ag+ T2AgRAg+ T2Ag(RAg)2+ ... + T2Ag(RAg)n + ... Rtotal= R+T2Ag / (1- AgR) Ttotal= T+TAgR+ T(AgR)2+ ... + T(AgR)n + ... Ttotal = T / (1- AgR) Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Features of a Cloud above a Reflecting Ground I (0) I0 R T2Ag T2AgRAg T2Ag(RAg)2 T2Ag(RAg)n TAgRAgRAg TAg TAgRAg T(AgR)n TAg (AgR)n TAgR T TAgRAgR ground has reflectance, (or albedo) = Ag. Ag=0 Rtotal= R, Ttotal = T General Relationship: Rtotal= R+T2Ag /(1- AgR) Ag=1 Rtotal= R +T2 /(1- R) Ttotal = T/(1-R) Ttotal = T / (1- AgR) Cloud Absorption, A Atotal= (In - Out)/I0 Ag=1, R+T=1 (conservative case) Rtotal= 1 Ttotal = 1 Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Weirdest thing (study the Ag = 1 case, R + T = 1 conservative case) I (0) I0 R T2 T2R T2(R)2 T2(R)n T TRR TR T(R)n T TR TRR T(R)n ground has reflectance, (or albedo) = Ag=1 in this case. Ag=1 Rtotal= R +T2 /(1- R) Ttotal = T/(1-R) Let R=0.99. With 100 photons incident, 99 immediately reflect upwards and are lost. One photon passes through and reflects 99 times between the ground and cloud before being lost by transmission to the upward direction. This is the basis of an optical buildup cavity and integrating spheres. Ag=1, R+T=1 (conservative case) Rtotal= 1 Ttotal = 1 Case shown: R 1. Radiation is trapped between the cloud and ground. A very small amount is reflected besides the first reflection. Energy is conserved because In = Out, or 1 = Rtotal Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Conservative Case: Example of Ttotal Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Energy Conservation for the Conservative Case I (0) I0 R T2Ag T2AgRAg T2Ag(RAg)2 T2Ag(RAg)n TAgRAgRAg TAg TAgRAg T(AgR)n TAg (AgR)n TAgR T TAgRAgR ground has reflectance, (or albedo) = Ag. Energy Conservation: In to system = Out of system 1= Rtotal+ Agnd = 1 General Relationship: Rtotal= R+T2Ag /(1- AgR) Ttotal = T / (1- AgR) (can show with algebra) Total Absorption by Ground, Agnd Agnd= (Ingnd - Outgnd)/I0 Agnd = Ttotal (1- Ag) Can show with algebra, or by inspection Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
Additional Relationships and Limits for the General Case: deep multiple scattering with some absorption Pat Arnott, ATMS 749 Atmospheric Radiation Transfer
An Example Pat Arnott, ATMS 749 Atmospheric Radiation Transfer