Quadratic Functions and Translations
In Section 4.1, explore quadratic functions in various forms and their translations. Understand the vertex form, axis of symmetry, and how graphs change with different coefficients. Dive into problems to visualize and analyze different quadratic functions through graphs and transformations. Enhance your understanding of parabolas and mirror images in quadratic functions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Section 4.1 Quadratic Functions and Translations
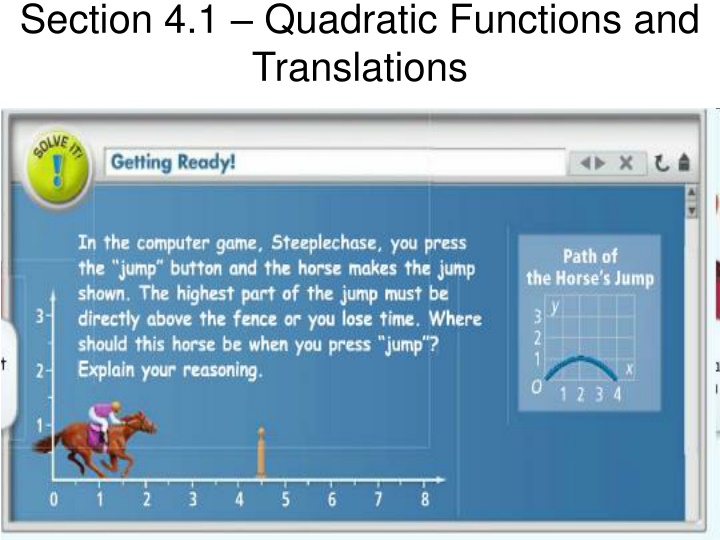
Section 4.1 Quadratic Functions and Translations In the Solve It, you used a parabolic shape of the horse s jump. A parabola is the graph of a quadratic function, which you can write in the form y = ax2+ bx + c, where a cannot be 0. Essential Understanding The graph of ANY quadratic function is a transformation of the graph of the parent quadratic function y = x2.
Section 4.1 Quadratic Functions and Translations The vertex form of a quadratic function is f(x) = a(x h)2+ k, where a cannot be 0. The axis of symmetry is a line that divides the parabola into two mirror images. The equation of the axis of symmetry is x = h. The vertex of the parabola is (h, k) the intersection of the parabola and its axis of symmetry.
Section 4.1 Quadratic Functions and Translations
Section 4.1 Quadratic Functions and Translations Problem 1: What is the graph of f(x) = x2
Section 4.1 Quadratic Functions and Translations Problem 1: What is the graph of f(x) = -1/3x2
Section 4.1 Quadratic Functions and Translations Graphs of y = ax2and y = -ax2are reflections of each other across the x-axis. Increasing |a| stretches the graph vertically and narrows it horizontally. Decreasing |a| compresses the graph vertically and widens it horizontally.
Section 4.1 Quadratic Functions and Translations
Section 4.1 Quadratic Functions and Translations Problem 2: Graph each function. How is each graph a translation of f(x) = x2 g(x) = x2 5
Section 4.1 Quadratic Functions and Translations Problem 2: Graph each function. How is each graph a translation of f(x) = x2 g(x) = (x 4)2
Section 4.1 Quadratic Functions and Translations Problem 2: Graph each function. How is each graph a translation of f(x) = x2 g(x) = x2+ 3
Section 4.1 Quadratic Functions and Translations Problem 2: Graph each function. How is each graph a translation of f(x) = x2 g(x) = (x + 1)2
Section 4.1 Quadratic Functions and Translations The vertex form, f(x) = a(x h)2+ k, gives you information about the graph of f without drawing the graph. If a > 0, k is the minimum value of the function. If a < 0, k is the maximum value.
Section 4.1 Quadratic Functions and Translations Problem 3: For y = 3(x 4)2 2, what are the vertex, the axis of symmetry, the maximum or minimum value, the domain and range?
Section 4.1 Quadratic Functions and Translations Problem 3: For y = -2(x + 1)2+ 4, what are the vertex, the axis of symmetry, the maximum or minimum value, the domain and range?
Section 4.1 Quadratic Functions and Translations You can use the vertex of a quadratic function, f(x) = a(x h)2+ k, to transform the graph of the parent function f(x) = x2. Stretch or compress the graph of f(x) = x2 vertically by a factor of |a| If a < 0, reflect the graph across the x-axis Shift the graph |h| units horizontally and |k| units vertically
Section 4.1 Quadratic Functions and Translations
Section 4.1 Quadratic Functions and Translations Problem 4: What is the graph of f(x) = -2(x 1)2+ 3?
Section 4.1 Quadratic Functions and Translations Problem 4: What is the graph of f(x) = 2(x +2)2 5 ?
Section 4.1 Quadratic Functions and Translations Problem 5: Write an equation of the parabola through Vertex(1, 2) Point(2, -5)
Section 4.1 Quadratic Functions and Translations Problem 5: Write an equation of the parabola through Vertex(-3, 6) Point(1, -2)
Section 4.1 Quadratic Functions and Translations Problem 5: Write an equation of the parabola through Vertex(0, 5) Point(1, -2)
Section 4.1 Quadratic Functions and Translations Problem 6: A gardener is putting a wire fence along the edge of his garden to keep animals from eating his plants. If he has 20 meters of fence, what is the largest rectangular area he can enclose?
Section 4.1 Quadratic Functions and Translations Problem 6: Write a quadratic function to represent the areas of all rectangles with a perimeter of 36 feet. Graph the function and describe the rectangle that has the largest area.