Properties of Exponents and Logarithms
The rules of exponents and logarithms through properties such as the Product Rule, Quotient Rule, Power Rule, and more. Learn how to apply these properties to determine the truth of statements using logarithms. Utilize your calculator to verify the results and practice expanding expressions using logarithmic properties.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
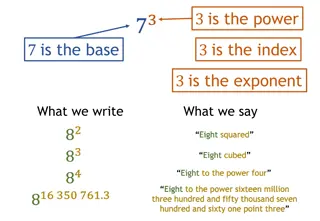
These properties are based on rules of exponents since logs = exponents
I. ????1 = 0 Because in exponential form ?0= 1 (any number to the zero power = 1) 0 Example: ????1= 0 Example: ???51= 5 to what power = 1?
II. ????? = 1 Because in exponential form ?1= ? (any number to the first power is itself) 1 Example: ?????=1 Example: ???55= 5 to what power = 5?
III. Product Rule ?????? = ????? + ????? Because in exponential form ?? ??= ??+? Examples: ?????? =????? + ????? ???6 = ???2 + ???3 ???39? = ???39 + ???3?
IV. Quotient Rule ? ?= ????? ????? Because in exponential form?? ???? ??= ?? ? ? ? =???5? ???5? ???2? ???23 Examples: ???5 ? 3 = ???2 6? 7= ???3 ????? + ????? ?????
V. Power Rule ??????= ?????? Because in exponential form ?? ?= ??? Examples: ???5?3 = 3???5? ???2?3?4= 3???2? + 4???2?
VI. Change of Base Formula ????? =???? ???? ???9 ???5 Example: ???59 = These properties remain the same when working with the natural log.
Use properties of logarithms to determine if each of the following is true or false. Check your answers using your calculator ) 3 = + = ) 2 True True False False log( 2 log 2 log 3 log 6 log 2 log( 6 ________1) ______ 2) = 5 3 True True 5 log 4 log( 4 ) ________ 3) = log log 3 log 5 True True ______ 4) 5 + = ) 6 + False False log( ) 5 log( ) 6 log( 5 False False = + 4 log( 2 3 ) (log 4 2 log ) 3 _______6) ________ 5) = ) 6 + log 5 log 6 log( 5 log 3 ______ 8) False False = False False log 3 log 5 ________ 7) log 5 log 8 = 3 True True log 2 ( 2 ) 3 ______ 10) = True True log2 8 ________ 9) log 2 True True True True = = + ln 2 log 2 4 log( 2 3 ) log 2 4 log 3 ______ 12) _______ 11) e
Use the properties of logs to expand the following expressions: ) 5 log( x 1. 3y 1. Apply Product Rule: + 3+ log 5 log log x y + + log 5 3 log log x y 2. Apply Power Rule:
Use the properties of logs to expand the following expressions: 5 log 4 ( 2 ) xy 2. 1. Apply Product Rule: + x+ 5 log 4 log log y 2 2 2 + + log 4 log 5 log x y 2. Apply Power Rule: 2 2 2
Use the properties of logs to expand the following expressions: z xy log 3. 10 1. Apply Quotient Rule: log log xy z 10 10 + log log log x y z 2. Apply Product Rule: 10 10 10
Use the properties of logs to expand the following expressions: ( a b 5 log ) 4. 1 1. Change radical to exponential form: log ba 2 5 2. Apply Product Rule: 1 b+ log log a 2 5 5 1 + log log b a 3. Apply Power Rule: 5 5 2
Use the properties of logs to expand the following expressions: ( ln y x ) 2 5 5. + 2 5 ln ln x y 2. Apply Product Rule: 2 ln 5 ln x y 3. Apply Power Rule:
Practice Time Practice Time
Write as a single logarithmic expression. log 3 log 2 1 ( ) 1 + x x 1. 10 10 1. Apply Reverse Power Rule: 1 ) 1 + 3 log log 1 ( x x 2 10 10 2. Apply Reverse Quotient Rule: x 2 log 10 ) 1 + 3 ( x x log 3. Change to radical form 10 ) 1 + 3 ( x
Write as a single logarithmic expression. log ) 2 ( log 5 + + x ( ) 2 x 2. 1. Apply Reverse Product Rule: 5 + log5 ( 2 )( ) 2 x x 2. Simplify 2 log ( ) 4 x 5
Write as a single logarithmic expression. x + 1. Apply Reverse Power Rule: 5 ln( ) 3 ln( ) y 3. x + 5 3 ln ln y 2. Apply Reverse Product Rule: 5y 3 ln( ) x
( ) 3 3 a log ab log 3 b ( ) z 1 1 5 3 = = ln x y log log log a a a 2 2
+ + (log 3 log( )) log log 3 log x y z a b c 3 ( ) xy a log log +c 3 b z 1 3 log log x y + + log ( ) log ( ) x y x y 2 x3 2 2 x 2 2 log ( ) y log 2 y 5 log 6 log a b log 4 3 3 log 5 5 a log5 4 log 3 6 b
More Practice Time More Practice Time