Laws of Exponents and Their Applications

Laws of exponents are essential rules for manipulating expressions with variables and exponents having the same base. These laws allow for simplification and manipulation of expressions by following specific rules regarding exponents and bases. Various examples and properties demonstrate the practical application of these laws, aiding in solving mathematical problems efficiently.

• Exponents
• Math
• Rules
• Applications
• Laws

kay_hen Follow

Uploaded on Oct 07, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

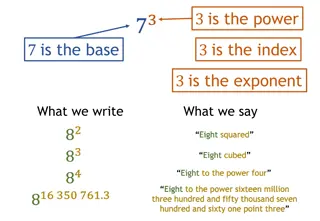
1. Laws of Exponents Whenever we have variables which contain exponents and have equal bases, we can do certain mathematical operations to them. Those operations are called the Laws of Exponents bx b = base x = exponent

2. Laws of Exponents = ( ) xy m + = m n m n m m . 1 . 2 x x x x y m ( ) x m x x n = = m mn . 3 . 4 x m y y m x = m n 5 . , a if m n then x n x m 1 x = 5 . , b if n m then n n m x x

3. Other Properties of Exponents 1 0= 1 x 1= x x Any single number or variable is always to the first power ( )1 = = = = 1 1 1 1 3 3 2 2 2 a a x x x

4. Basic Examples = +3 = 2x 3 2x x 5x ( ) = x 3 3 4 = 4x 12 x ( ) = xy 3y 3 3 x

5. Basic Examples 3 3 x x = 3 y y 7 7 4 x x = = 3x 4 1 x x 5 1 x 1 = = 7 5 7 2 x x

6. More Examples = 14a ) 2 8 r = 2 m ( ) +4 2 = 3 37 r 4 7 2 r 7 = 2 ( 2 a ( a 5 a 8 + + = = 2 3 2 3 2 7 5 2 80r r ) = 3 12 3 2 3 5 3 3 6 15 6 15 2 5 8 m n n m n m n ( ) = = 33 3 3 3 3 3 27 x y x y 3xy 2 2 2 2 2 a 2 4 a a = = 2 2 2 3 x 9 3 x 2 9 b 4 b b 4 1 8 8 = = 3 4x 2 9 1 1 x 3 z 3 x 1 = = = 3x 3 5 2 5 2 3 z 3 z

7. More Examples ( ) + + + = = 4 3 3 3 2 2 3 1 2 1 1 2 21 3 7 3 7 x y z x y z xyz x y z ( )= ( ) + + + + = 2 3 1 1 1 2 1 3 3 6 8 3 2 8 3 2 48 xy xy xy x y x y ( )( )= ( ) ( ) = 2 2 1 2 2 2 3 2 1 2 1 2 2 2 2 3 2 3 2 x y x y 3 2 x y xy ( ) + + = = 4 6 2 4 4 2 6 4 6 10 9 4 9 4 36 x y x y x y x y 3 3 9 3 9 3 1 3 3 3 1 3 9 3 6 3 5 125 5 125 125 a b a a b a b a 5 a b = = = = = 3 3 6 6 3 1 3 1 3 2 3 3 6 3 2 3 27 3 27 27 a b b a b a b b 3 ab

8. This powerpoint was kindly donated to www.worldofteaching.com http://www.worldofteaching.com is home to over a thousand powerpoints submitted by teachers. This is a completely free site and requires no registration. Please visit and I hope it will help in your teaching.