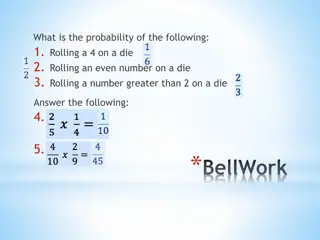Probability and Independent Events Study

Explore probabilities based on a table showing preferences for fast food restaurants and learn about independent events through various experiments like coin tossing and card picking. Understand conditional probabilities and connections to independence.

• Probability
• Independent Events
• Conditional Probability
• Fast Food
• Experiments

woodberry_c Follow

Uploaded on Feb 21, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Warm up The following table shows the number of people that like a particular fast food restaurant. McDonald s Burger King 15 Wendy s Male 20 10 Female 20 10 25 7/20 1) What is the probability that a person likes Wendy s? 3/5 2) What is the probability that a person is male given they like Burger King? 3/4 3. What is the probability that a randomly chosen person is female or likes McDonald s?

2. CCGPS Geometry UNIT QUESTION: What connection does conditional probability have to independence? Standard: MCC9-12.S.CP.1-7 Today s Question: How can I determine if 2 events are independent of each other? Standard: MCC9-12.S.CP.1, 7

3. Probability Independent vs. Dependent events

4. Independent Events Two events A and B, are independent if the fact that A occurs does not affect the probability of B occurring. Examples- Landing on heads from two different coins, rolling a 4 on a die, then rolling a 3 on a second roll of the die. Probability of A and B occurring: P(A and B) = P(A) P(B)

5. Experiment 1 A coin is tossed and a 6-sided die is rolled. Find the probability of landing on the head side of the coin and rolling a 3 on the die. P (head) = 1/2 P(3) = 1/6 P (head and 3) = P (head) P(3) = 1/2 1/6 = 1/12

6. Experiment 2 A card is chosen at random from a deck of 52 cards. It is then replaced and a second card is chosen. What is the probability of choosing a jack and an eight? P (jack) = 4/52 P (8) = 4/52 P (jack and 8) = 4/52 4/52 = 1/169

7. Experiment 3 A jar contains three red, five green, two blue and six yellow marbles. A marble is chosen at random from the jar. After replacing it, a second marble is chosen. What is the probability of choosing a green and a yellow marble? P (green) = 5/16 P (yellow) = 6/16 P (green and yellow) = P (green) P (yellow) = 15 / 128

8. Experiment 4 A school survey found that 9 out of 10 students like pizza. If three students are chosen at random with replacement, what is the probability that all three students like pizza? P (student 1 likes pizza) = 9/10 P (student 2 likes pizza) = 9/10 P (student 3 likes pizza) = 9/10 P (student 1 and student 2 and student 3 like pizza) = 9/10 9/10 9/10 = 729/1000

9. Dependent Events Two events A and B, are dependent if the fact that A occurs affects the probability of B occurring. Examples- Picking a blue marble and then picking another blue marble if I don t replace the first one. Probability of A and B occurring: P(A and B) = P(A) P(B given A)

10. Experiment 1 A jar contains three red, five green, two blue and six yellow marbles. A marble is chosen at random from the jar. A second marble is chosen without replacing the first one. What is the probability of choosing a green and a yellow marble? P (green) = 5/16 P (yellow given green) = 6/15 P (green and then yellow) = P (green) P (yellow) = 1/8

11. Experiment 2 An aquarium contains 6 male goldfish and 4 female goldfish. You randomly select a fish from the tank, do not replace it, and then randomly select a second fish. What is the probability that both fish are male? P (male) = 6/10 P (male given 1st male) = 5/9 P (male and then, male) = 1/3 goldfish

12. Experiment 3 A random sample of parts coming off a machine is done by an inspector. He found that 5 out of 100 parts are bad on average. If he were to do a new sample, what is the probability that he picks a bad part and then, picks another bad part if he doesn t replace the first? P (bad) = 5/100 P (bad given 1st bad) = 4/99 P (bad and then, bad) = 1/495

13. Independent vs. Dependent Determining if 2 events are independent

14. Independent Events Two events are independent if the following are true: P(A|B) = P(A) P(B|A) = P(B) P(A AND B) = P(A) P(B) To show 2 events are independent, you must prove one of the above conditions.

15. Experiment 1 Let event G = taking a math class. Let event H = taking a science class. Then, G AND H = taking a math class and a science class. Suppose P(G) = 0.6, P(H) = 0.5, and P(G AND H) = 0.3. Are G and H independent? ( ) P G H 0.3 = = 0.6 0.5 ( ) P G ( )? P H

16. Experiment 2 In a particular college class, 60% of the students are female. 50% of all students in the class have long hair. 45% of the students are female and have long hair. Of the female students, 75% have long hair. Let F be the event that the student is female. Let L be the event that the student has long hair. One student is picked randomly. Are the events of being female and having long hair independent? = 0.45 0.45 0.6 0.5 0.3 = ( ) ( ) P F ( )? P L P F L

17. Homework Practice Worksheet