Pairwise Distance and Graph-Based Clustering Overview
Explore the concept of clustering through graph cuts and pairwise distances. Understand how clustering can be achieved via graph cuts and the implications of cutting based on class or cluster labels. Learn about external validation and the k-means clustering algorithm. Dive into partitional clustering algorithms that partition instances into non-overlapping clusters, optimizing criteria such as inter-cluster and intra-cluster distances. Discover the challenges and alternatives in optimizing partitional clustering effectively.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
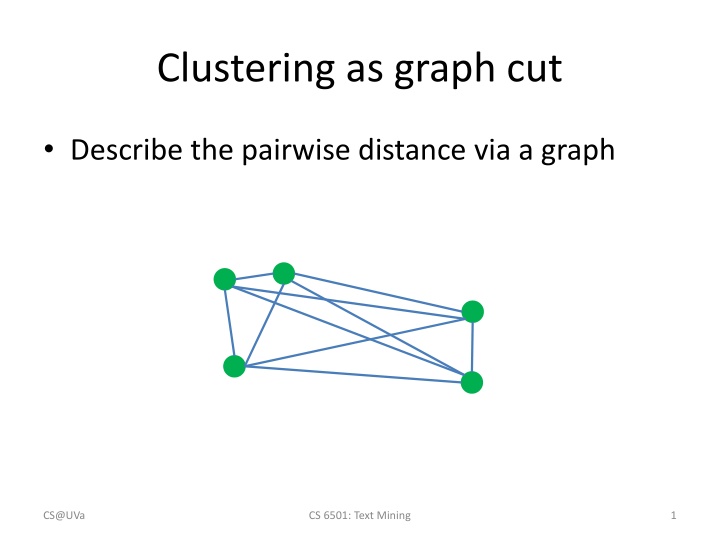
Clustering as graph cut Describe the pairwise distance via a graph CS@UVa CS 6501: Text Mining 1
Clustering as graph cut Describe the pairwise distance via a graph Clustering can be obtained via graph cut CS@UVa CS 6501: Text Mining 2
Clustering as graph cut Describe the pairwise distance via a graph Clustering can be obtained via graph cut CS@UVa CS 6501: Text Mining 3
Clustering as graph cut Describe the pairwise distance via a graph Clustering can be obtained via graph cut Cut by class label Cut by cluster label CS@UVa CS 6501: Text Mining 4
Recap: external validation Given class label on each instance Rand index ??= wj ?? wj ??= ?? 20 20 ?? ?? 24 72 6 2 6 2 5 2 5 2 4 2 3 2 2 2 ?? + ?? = + + = 40 ?? = + + + = 20 CS@UVa CS 6501: Text Mining 5
k-means Clustering Hongning Wang CS@UVa
Todays lecture k-means clustering A typical partitional clustering algorithm Convergence property Expectation Maximization algorithm Gaussian mixture model CS@UVa CS 6501: Text Mining 7
Partitional clustering algorithms Partition instances into exactly k non- overlapping clusters Flat structure clustering Users need to specify the cluster size k Task: identify the partition of k clusters that optimize the chosen partition criterion CS@UVa CS 6501: Text Mining 8
Partitional clustering algorithms Partition instances into exactly k non- overlapping clusters Typical criterion max ? j? ??,?? ? ??? Optimal solution: enumerate every possible partition of size k and return the one maximizes the criterion Optimize this in an alternative way Inter-cluster distance Intra-cluster distance Let s approximate this! Unfortunately, this is NP-hard! CS@UVa CS 6501: Text Mining 9
k-means algorithm ?, distance metric ?( , ) ? Input: cluster size k, instances {??}?=1 Output: cluster membership assignments {??}?=1 1. Initialize k cluster centroids {??}?=1 domain knowledge is available) 2. Repeat until no instance changes its cluster membership: Decide the cluster membership of instances by assigning them to the nearest cluster centroid ??= ????????(??,??) Update the k cluster centroids based on the assigned cluster membership ??= ?? ??= ???? ??(??= ??) ? (randomly if no Minimize intra distance Maximize inter distance CS@UVa CS 6501: Text Mining 10
k-means illustration CS@UVa CS 6501: Text Mining 11
k-means illustration Voronoi diagram CS@UVa CS 6501: Text Mining 12
k-means illustration CS@UVa CS 6501: Text Mining 13
k-means illustration CS@UVa CS 6501: Text Mining 14
k-means illustration CS@UVa CS 6501: Text Mining 15
Complexity analysis Decide cluster membership ?(??) Compute cluster centroid ?(?) Assume k-means stops after ? iterations ?(???) Don t forget the complexity of distance computation, e.g., ?(?) for Euclidean distance CS@UVa CS 6501: Text Mining 16
Convergence property Why will k-means stop? Answer: it is a special version of Expectation Maximization (EM) algorithm, and EM is guaranteed to converge However, it is only guaranteed to converge to local optimal, since k-means (EM) is a greedy algorithm CS@UVa CS 6501: Text Mining 17
Probabilistic interpretation of clustering The density model of ? ? is multi-modal Each mode represents a sub-population E.g., unimodal Gaussian for each group ?(?|? = 2) Mixture model ?(?|? = 1) ? ? = ? ? ? ?(?) ? Unimodal distribution Mixing proportion ?(?|? = 3) CS@UVa CS 6501: Text Mining 18
Probabilistic interpretation of clustering If ? is known for every ? Estimating ?(?) and ?(?|?) is easy Maximum likelihood estimation This is Na ve Bayes ?(?|? = 2) Mixture model ?(?|? = 1) ? ? = ? ? ? ?(?) ? Unimodal distribution Mixing proportion ?(?|? = 3) CS@UVa CS 6501: Text Mining 19
Probabilistic interpretation of clustering Usually a constrained optimization problem But ? is unknown for all ? Estimating ?(?) and ?(?|?) is generally hard max ?,? ?log ??? ????,? ?(??|?) Appeal to the Expectation Maximization algorithm ? ? ? = 2 ? Mixture model ? ? ? = 1 ? ? ? = ? ? ? ?(?) ? Unimodal distribution Mixing proportion ? ? ? = 3 ? CS@UVa CS 6501: Text Mining 20
Introduction to EM Parameter estimation All data is observable Maximum likelihood estimator Optimize the analytic form of ? ? = log?(?|?) Missing/unobservable data Data: X (observed) + Z (hidden) Likelihood: ? ? = log ?? ?,? ? Approximate it! E.g. cluster membership Most of cases are intractable CS@UVa CS 6501: Text Mining 21
Background knowledge Jensen's inequality For any convex function ?(?) and positive weights ?, ? ???? ???(??) ??= 1 ? ? ? CS@UVa CS 6501: Text Mining 22
Expectation Maximization Maximize data likelihood function by pushing the lower bound Proposal distributions for ? ? ? ? ?,Z ? ? ? ? ? = log ?? ?,Z ? = log ? Jensen's inequality ? ? ? ?[?(?)] ?? ? log? ?,? ? ?? ? log?(?) Lower bound! Components we need to tune when optimizing ? ? : ?(?) and ?! CS@UVa CS 6501: Text Mining 23
Intuitive understanding of EM Data likelihood p(X| ) Easier to optimize, guarantee to improve data likelihood Lower bound CS@UVa CS 6501: Text Mining 24
Expectation Maximization (cont) Optimize the lower bound w.r.t. ?(?) ? ? ?? ? ???? ?,? ? ?? ? ????(?) = ?? ? log? ? ?,? + log?(?|?) ?? ? log? ? ?,? ?(?) ?? ? log?(?) = + log?(?|?) Constant with respect to ?(?) negative KL-divergence between ?(?) and ? ? ?,? ??(?| ? = ? ? log?(?) ?(?)?? CS@UVa CS 6501: Text Mining 25
Expectation Maximization (cont) Optimize the lower bound w.r.t. ?(?) ? ? ?? ?(?)||? ? ?,? KL-divergence is non-negative, and equals to zero i.f.f. ? ? = ? ? ?,? A step further: when ? ? = ? ? ?,? , we will get ? ? ?(?), i.e., the lower bound is tight! Other choice of ? ? cannot lead to this tight bound, but might reduce computational complexity Note: calculation of ? ? is based on current ? + ?(?) CS@UVa CS 6501: Text Mining 26
Expectation Maximization (cont) Optimize the lower bound w.r.t. ?(?) Optimal solution: ? ? = ? ?|?,?? Posterior distribution of ? given current model ?? In k-means: this corresponds to assigning instance ?? to its closest cluster centroid ?? ??= ????????(??,??) CS@UVa CS 6501: Text Mining 27
Expectation Maximization (cont) Optimize the lower bound w.r.t. ? ? ? ?? ?|?,??log? ?,? ? ?? ?|?,??log? ?|?,?? ??+1= ??????? ?? ?|?,?????? ?,? ? Constant w.r.t. ? = ?????????|?,?? log?(?,?|?) Expectation of complete data likelihood In k-means, we are not computing the expectation, but the most probable ?? ??=???? ??(??=??) configuration, and then ??= CS@UVa CS 6501: Text Mining 28
Expectation Maximization EM tries to iteratively maximize likelihood Complete data likelihood: ??? = log?(?,Z|?) Starting from an initial guess (0), 1. E-step: compute the expectation of the complete data likelihood ? ?;??= E?|?,?? ??? ?? ? ?,??log p X,Z ? = 2. M-step: compute (t+1) by maximizing the Q-function ??+1= ???????? ?;?? Key step! CS@UVa CS 6501: Text Mining 29
An intuitive understanding of EM In k-means E-step: identify the cluster membership - ? ? ?,? M-step: update ? by ? ? ?,? Data likelihood p(X| ) next guess current guess Lower bound (Q function) E-step = computing the lower bound M-step = maximizing the lower bound 30 CS@UVa CS 6501: Text Mining
Convergence guarantee Proof of EM log? ? ? = log? ?,? ? log?(?|?,?) Taking expectation with respect to ?(?|?,??) of both sides: ??(?|?,??)log? ?,? ? = ? ?;??+ ?(?;??) ??(?|?,??)log?(?|?,?) Cross-entropy log? ? ? = Then the change of log data likelihood between EM iteration is: log? ? ? log?(?|??) = ? ?;??+ ? ?;?? ? ??;?? ?(??;??) By Jensen s inequality, we know ? ?;?? ? ??;??, that means log? ? ? log?(?|??) ? ?;?? ? ??;?? 0 M-step guarantee this CS@UVa CS 6501: Text Mining 31
What is not guaranteed Global optimal is not guaranteed! Likelihood: ? ? = log ?? ?,Z ? is non-convex in most of cases EM boils down to a greedy algorithm Alternative ascent Generalized EM E-step: ? ? = argmin?(?)?? ?(?)||? ? ?,?? M-step: choose ? that improves ? ?;?? CS@UVa CS 6501: Text Mining 32
k-means v.s. Gaussian Mixture If we use Euclidean distance in k-means We have explicitly assumed ?(?|?) is Gaussian Gaussian Mixture Model (GMM) ? ? ? = ? ??, ? ? ? = ?? Multinomial ? 1 1 2?? ? ???(? ??) 1 2? ??? z 1? ?? 2 ? ? ? = ? ? ? = 2?? ? In k-means, we assume equal variance across clusters, so we don t need to estimate them We do not consider cluster size in k-means CS@UVa CS 6501: Text Mining 33
k-means v.s. Gaussian Mixture Soft v.s., hard posterior assignment GMM k-means CS@UVa CS 6501: Text Mining 34
k-means in practice Extremely fast and scalable One of the most popularly used clustering methods Top 10 data mining algorithms ICDM 2006 Can be easily parallelized Map-Reduce implementation Mapper: assign each instance to its closest centroid Reducer: update centroid based on the cluster membership Sensitive to initialization Prone to local optimal CS@UVa CS 6501: Text Mining 35
Better initialization: k-means++ 1. Choose the first cluster center at uniformly random 2. Repeat until all k centers have been found For each instance compute Dx= min k?(?,??) Choose a new cluster center with probability ? ? ?? 3. Run k-means with selected centers as initialization 2 new center should be far away from existing centers CS@UVa CS 6501: Text Mining 36
How to determine k Vary ? to optimize clustering criterion Internal v.s. external validation Cross validation Abrupt change in objective function CS@UVa CS 6501: Text Mining 37
How to determine k Vary ? to optimize clustering criterion Internal v.s. external validation Cross validation Abrupt change in objective function Model selection criterion penalizing too many clusters AIC, BIC CS@UVa CS 6501: Text Mining 38
What you should know k-means algorithm An alternative greedy algorithm Convergence guarantee EM algorithm Hard clustering v.s., soft clustering k-means v.s., GMM CS@UVa CS 6501: Text Mining 39
Todays reading Introduction to Information Retrieval Chapter 16: Flat clustering 16.4 k-means 16.5 Model-based clustering CS@UVa CS 6501: Text Mining 40