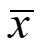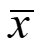The Central Limit Theorem in Statistics
This lesson covers the Central Limit Theorem, which states that the sampling distribution of a sample mean becomes approximately normal as the sample size increases, regardless of the population distribution. It explains how the distribution of sample means changes shape and approaches a normal distribution with a finite standard deviation in the population. The application of the Central Limit Theorem in estimating population parameters from sample means is illustrated through a practical example involving air-conditioning unit maintenance times.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Sampling Distributions Lesson 6.6 The Central Limit Theorem Statistics and Probability with Applications, 3rdEdition Starnes & Tabor Starnes & Tabor Statistics and Probability with Applications, 3rd Edition Bedford Freeman Worth Publishers Bedford Freeman Worth Publishers
The Central Limit Theorem Learning Targets After this lesson, you should be able to: After this lesson, you should be able to: Learning Targets Determine if the sampling distribution of x is approximately normal when sampling from a non-normal population. If appropriate, use a normal distribution to calculate probabilities involving . x Statistics and Probability with Applications, 3rd Edition 2 2
The Sampling Distribution of a Sample Mean When sample data are categorical, we often use the count or proportion of successes in the sample to make an inference about a population. When sample data are quantitative, we often use the sample mean x to estimate the mean of a population. Sampling Distribution of the Sample Mean x Statistics and Probability with Applications, 3rd Edition 3 3
The Central Limit Theorem Most population distributions are not Normal. What is the shape of the sampling distribution of sample means when the population distribution isn t Normal? It is a remarkable fact that as the sample size increases, the distribution of sample means changes its shape: it looks less like that of the population and more like a Normal distribution! When the sample is large enough, the distribution of sample means is very close to Normal, no matter what shape the population distribution has, as long as the population has a finite standard deviation. Central Limit Theorem (CLT) Statistics and Probability with Applications, 3rd Edition 4 4
The Central Limit Theorem Normal/Large Sample Condition Statistics and Probability with Applications, 3rd Edition 5 5
LESSON APP 6.6 Keeping things cool with statistics? Your company has a contract to perform preventive maintenance on thousands of air-conditioning units in a large city. Based on service records from the past year, the time (in hours) that a technician requires to complete the work follows a strongly right-skewed distribution with = 1 hour and = 1.5 hours. As a promotion, your company will provide service to a random sample of 70 air-conditioning units free of charge. You plan to budget an average of 1.1 hours per unit for a technician to complete the work. Will this be enough time? Statistics and Probability with Applications, 3rd Edition 6 6
The Central Limit Theorem Learning Targets After this lesson, you should be able to: After this lesson, you should be able to: Learning Targets Determine if the sampling distribution of x is approximately normal when sampling from a non-normal population. If appropriate, use a normal distribution to calculate probabilities involving . x Statistics and Probability with Applications, 3rd Edition 7 7