Multiple Steady States in CSTR Reactors
Review: Multiple Steady States in
CSTR
•
Plot of X
A,EB
vs T and X
A,MB
vs T
•
Intersections are the T and X
A
that satisfy both mass balance (MB) &
energy balance (EB) equations
•
Each intersection is a steady state
(temperature & conversion)
•
Multiple sets of conditions are possible for the same reaction in the same
reactor with the same inlet conditions!
X
A,MB
For
T
a
< T
0
Review: Heat Removal Term R(T) & T
0
Heat removed:
R(T)
Heat generated
G(T)
When T
0
increases, slope stays
same & line shifts to right
R(T) line has slope of C
P0
(1+
)
When
increases from lowering
F
A0
or increasing heat exchange,
slope and x-intercept moves
T
a
<T
0
: x-intercept shifts left as
↑
T
a
>T
0
: x-intercept shifts right as
↑
=0, then T
C
=T
0
=
∞
, then T
C
=T
a
Review: CSTR Stability
1
2
3
R(T)
>
G(T)
→
T
falls to T=SS
1
G(T)
>
R(T)
→
T rises to
T=SS
3
G(T)
>
R(T)
→
T rises to
T=SS
1
R(T)
>
G(T)
→
T falls to T=SS
3
•
Magnitude of
G(T)
to
R(T)
curve determines if reactor T will rise or fall
•
G(T)
=
R(T)
intersection, equal rate of heat generation & removal, no
change in T
•
G(T)
>
R(T)
(
G(T)
line above
R(T)
on graph): rate of heat generation > heat
removal, so reactor heats up until a steady state is reached
•
R(T)
>
G(T)
(
R(T)
line above
G(T)
on graph): rate of heat generation < heat
removal, so reactor cools off until a steady state is reached
H
e
a
t
g
e
n
e
r
a
t
e
d
G
(
T
)
H
e
a
t
r
e
m
o
v
e
d
:
R
(
T
)
L16: Unsteady State Nonisothermal
Reactor Design
An open system (for example, CSTR)
Goal: develop EB for unsteady state reactor
Change in System Energy with Time
E
n
e
r
g
y
o
f
s
y
s
t
e
m
i
s
t
h
e
s
u
m
o
f
p
r
o
d
u
c
t
s
o
f
e
a
c
h
s
p
e
c
i
e
s
s
p
e
c
i
f
i
c
e
n
e
r
g
y
E
i
&
t
h
e
m
o
l
e
s
o
f
e
a
c
h
s
p
e
c
i
e
s
:
D
i
f
f
e
r
e
n
t
i
a
t
e
w
r
t
t
i
m
e
Total Energy Balance for unsteady state, constant PV
F
o
r
w
e
l
l
-
m
i
x
e
d
r
e
a
c
t
o
r
w
i
t
h
c
o
n
s
t
a
n
t
P
V
-
v
a
r
i
a
t
i
o
n
0
Well-Mixed Reactors, Constant PV
S
p
e
c
i
a
l
c
a
s
e
:
w
e
l
l
-
m
i
x
e
d
r
e
a
c
t
o
r
s
(
e
.
g
.
,
b
a
t
c
h
,
C
S
T
R
o
r
s
e
m
i
b
a
t
c
h
)
w
i
t
h
c
o
n
s
t
a
n
t
P
V
-
v
a
r
i
a
t
i
o
n
i
n
t
o
t
a
l
P
o
r
V
c
a
n
b
e
n
e
g
l
e
c
t
e
d
Total Energy Balance for unsteady state, constant PV
Total Energy Balance for unsteady state
Need to put dN
i
/dt into terms that can be measured
EB for Well-Mixed Reactors,
PV=0
From the mass balance:
S
u
b
s
t
i
t
u
t
e
A
d
d
F
i
H
i
t
o
b
o
t
h
s
i
d
e
s
o
f
e
q
u
a
t
i
o
n
:
S
u
b
s
t
i
t
u
t
e
Σ
i
H
i
=
H
°
R
X
(
T
)
:
Simplified EB for Well-Mixed Reactors
B
r
i
n
g
F
i
0
H
i
a
n
d
H
°
R
X
(
T
)
t
e
r
m
s
t
o
o
t
h
e
r
s
i
d
e
o
f
e
q
u
a
t
i
o
n
:
Solve for dT/dt:
F
a
c
t
o
r
F
i
0
H
i
0
a
n
d
F
i
0
H
i
t
e
r
m
s
a
n
d
d
i
v
i
d
e
b
y
N
i
C
p
i
:
Energy balance for
unsteady state reactor
with phase change:
Energy balance for
unsteady state reactor
without
phase change:
Unsteady State EB, Liquid-Phase Rxns
For liquid-phase reactions, often
C
p
=
i
C
pi
is so small it can be neglected
When
C
p
can be neglected, then:
I
f
t
h
e
f
e
e
d
i
s
w
e
l
l
-
m
i
x
e
d
,
i
t
i
s
c
o
n
v
e
n
i
e
n
t
t
o
u
s
e
:
P
l
u
g
t
h
e
s
e
e
q
u
a
t
i
o
n
s
a
n
d
T
i
0
=
T
0
i
n
t
o
t
h
e
E
B
g
i
v
e
s
:
This equation for the EB is simultaneously solved with the mass
balance (design eq) for unsteady state, nonisothermal reactor design
Nonisothermal Batch Reactor Design
No flow, so:
0
P
u
t
t
h
e
e
n
e
r
g
y
b
a
l
a
n
c
e
i
n
t
e
r
m
s
o
f
X
A
:
S
o
l
v
e
w
i
t
h
t
h
e
b
a
t
c
h
r
e
a
c
t
o
r
d
e
s
i
g
n
e
q
u
a
t
i
o
n
u
s
i
n
g
a
n
O
D
E
s
o
l
v
e
r
(
P
o
l
y
m
a
t
h
)
Adiabatic Nonisothermal Batch
Reactor Design
I
n
t
h
e
c
a
s
e
o
f
n
o
s
t
i
r
r
i
n
g
w
o
r
k
a
n
d
a
d
i
a
b
a
t
i
c
o
p
e
r
a
t
i
o
n
,
Substitute:
Rearrange:
Substitute:
0
0
G
e
t
l
i
k
e
t
e
r
m
s
t
o
g
e
t
h
e
r
:
S
o
l
v
i
n
g
f
o
r
T
:
S
o
l
v
e
w
i
t
h
t
h
e
b
a
t
c
h
r
e
a
c
t
o
r
d
e
s
i
g
n
e
q
u
a
t
i
o
n
u
s
i
n
g
a
n
O
D
E
s
o
l
v
e
r
(
P
o
l
y
m
a
t
h
)
I
n
t
e
g
r
a
t
e
&
s
o
l
v
e
f
o
r
X
A
:
Solve for how X
A
changes with T
A 1
st
order, liquid-phase, exothermic reaction A
→
B
is run in a batch reactor.
The reactor is well-insulated, so
no heat is lost to the surroundings
. To control
the temperature,
an inert liquid C is added to the reaction. The flow rate of C
is adjusted to keep T constant at 100
°F
. What is the flow rate of C after 2h?
This is essentially a semi-batch reactor since only
C is fed into the reactor
Design eq:
Rate eq:
-r
A
=
k
C
A
N
o
t
e
,
u
s
i
n
g
w
o
u
l
d
c
o
m
p
l
i
c
a
t
e
t
h
e
c
a
l
c
u
l
a
t
i
o
n
b
e
c
a
u
s
e
V
d
e
p
e
n
d
s
o
n
t
C
o
m
b
i
n
e
:
Rearrange and integrate for N
A
T
C0
= 80
°F
V
0
= 50 ft
3
H°
RX
=-25000 Btu/lb mol
k(100
°F)= 1.2 x 10
-4
s
-1
C
p,
(all components)= 0.5 Btu/lb mol °F
C
A0
= 0.5 lb mol/ft
3
1.
Solve design eq for comp as function of t
2.
Solve EB for F
C0
using that info & T=100 °F
Use EB to find how the flow rate of C depends on the rxn (solve EB for F
C0
)
A 1
st
order, liquid-phase, exothermic reaction A
→
B
is run in a batch reactor.
The reactor is well-insulated, so
no heat is lost to the surroundings
. To control
the temperature,
an inert liquid C is added to the reaction. The flow rate of C
is adjusted to keep T constant at 100
°F
. What is the flow rate of C after 2h?
C
i
s
t
h
e
o
n
l
y
s
p
e
c
i
e
s
t
h
a
t
f
l
o
w
s
,
s
o
:
r
A
V
=
-
k
C
A
V
=
-
k
N
A
0
0
0
I
s
o
l
a
t
e
F
C
0
:
A 1
st
order, liquid-phase, exothermic reaction A
→
B
is run in a batch reactor.
The reactor is well-insulated, so
no heat is lost to the surroundings
. To control
the temperature
, an inert liquid C is added to the reaction. The flow rate of C
is adjusted to keep
T constant at 100
°F
.
What is the flow rate of C after 2h
?
T
C0
= 80
°F
V
0
= 50 ft
3
H°
RX
=-25000 Btu/lb mol
k(100
°F)= 1.2 x 10
-4
s
-1
C
p,
(all components)= 0.5 Btu/lb mol °F
C
A0
= 0.5 lb mol/ft
3
At 2h (7200s):
Instead of feeding coolant to the reactor, a solvent with a low boiling point is
added (component D). The solvent has a
heat of vaporization of 1000 Btu/lb
mol
, and initially
25 lb mol of A
are placed in the tank. The reactor is well-
insulated. What is the rate of solvent evaporation after
2 h
if T is constant at 100
°F
?
S
t
i
l
l
a
s
e
m
i
b
a
t
c
h
r
e
a
c
t
o
r
,
w
h
e
r
e
D
i
s
r
e
m
o
v
e
d
f
r
o
m
t
h
e
r
e
a
c
t
o
r
U
s
e
E
B
t
h
a
t
a
c
c
o
u
n
t
s
f
o
r
a
p
h
a
s
e
c
h
a
n
g
e
:
Q
˙
=0
Ẇ
S
=0
0
0
0
Additional info:
k(100
°F)= 1.2 x 10
-4
s
-1
H
°
RX
=-25000 Btu/lb mol
Clicker Question:
Does dT/dt = 0?
a)
Yes
b)
No
Instead of feeding coolant to the reactor, a solvent with a low boiling point is
added (component D). The solvent has a
heat of vaporization of 1000 Btu/lb
mol
, and initially
25 lb mol of A
are placed in the tank. What is the rate of
solvent evaporation after
2 h
?
S
t
i
l
l
a
s
e
m
i
b
a
t
c
h
r
e
a
c
t
o
r
,
w
h
e
r
e
D
i
s
r
e
m
o
v
e
d
f
r
o
m
t
h
e
r
e
a
c
t
o
r
U
s
e
E
B
t
h
a
t
a
c
c
o
u
n
t
s
f
o
r
a
p
h
a
s
e
c
h
a
n
g
e
:
Q
˙
=0
Ẇ
S
=0
dT/dt = 0
D is the only species that ‘flows’,
and
r
A
V
=
-
k
N
A0
(exp[-kt])
, so:
0
0
0
Additional info:
k(100
°F)= 1.2 x 10
-4
s
-1
H
°
RX
=-25000 Btu/lb mol
A liquid phase exothermic reaction A
→B
is carried out at
358K
in a
0.2 m
3
CSTR
.
The coolant temperature is 273K and the heat transfer coefficient (U) is 7200
J/min·m
2
·K
. What is the heat exchange area required for steady state operation?
Using this heat exchange area, plot T vs t for reactor start-up.
C
PA
=C
PS
=20 J/g•K
Ẇ
S
=0 C
A0
= 180 g/dm
3
0
= 500 dm
3
/min
T
0
= 313 K
= 900 g/dm
3
H
°
RX
(T) = -2500 J/g
E=94852 J/mol
·K
k(313K)= 1.1 min
-1
a) Heat exchange area for steady state operation:
SS operation
means that T is
constant, so:
Q
˙
=
U
A
(
T
a
-
T
)
,
Ẇ
S
=
0
,
a
n
d
A
i
s
o
n
l
y
s
p
e
c
i
e
s
t
h
a
t
f
l
o
w
s
P
l
u
g
i
n
r
A
=
-
k
C
A
a
n
d
s
o
l
v
e
f
o
r
A
A liquid phase exothermic reaction A
→B
is carried out at
358K
in a
0.2 m
3
CSTR
.
The
coolant temperature is 273K
and the
heat transfer coefficient (U) is 7200
J/min
·
m
2
·K
. What is the heat exchange area required for steady state operation?
Using this heat exchange area, plot T vs t for reactor start-up.
C
PA
=C
PS
=20 J/
g•K
Ẇ
S
=0
C
A0
= 180 g/dm
3
0
= 500 dm
3
/min
T
0
= 313 K
= 900 g/dm
3
H
°
RX
(T) = -2500 J/g
E=94852 J/mol
·K
k(313K)= 1.1 min
-1
Use material balance to determine steady state value of C
A
A liquid phase exothermic reaction A
→B
is carried out at
358K
in a
0.2 m
3
CSTR
.
The coolant temperature is 273K and the heat transfer coefficient (U) is 7200
J/min
·
m
2
·K. What is the heat exchange area required for steady state operation?
Using this heat exchange area, plot T vs t for reactor start-up.
C
PA
=C
PS
=20 J/g•K Ẇ
S
=0 C
A0
= 180 g/dm
3
0
= 500 dm
3
/min
T
0
= 313 K
= 900 g/dm
3
H
°
RX
(T) = -2500 J/g
E=94852 J/mol
·K
k(313K)= 1.1 min
-1
Solve for heat exchange area at SS:
A=227.4 m
2
F
A0
=90,000 g/min
V=200 dm
3
H°
RX
(T) = -2500 J/g
k= 107.4 min
-1
C
A
= 4.1 g/dm
3
C
PA
=20 J/
g•K
U= 7200 J/min·m
2
·K
T
A0
= 313 K
T= 358K
T
a
=273K
Will use Polymath to plot T vs t for CSTR start-up (unsteady-state). Need
equations for dC
A
/dt, dT/dt, and k.
U= 7200
J/min·m
2
·K
A=227.4m
2
C
A0
=180g/
dm
3
=V/
0
T
a
=273K
H
RX
=-2500 J/g
N
i0
=m
i0
V=200 dm
3
C
Ps
=20 J/g
˙
K
0
=500 dm
3
T
0
=313
M
a
s
s
b
a
l
a
n
c
e
:
C
P
s
i
s
i
n
t
e
r
m
s
o
f
m
a
s
s
(
J
/
g
·
K
)
,
s
o
F
A
0
&
N
i
0
m
u
s
t
a
l
s
o
b
e
i
n
t
e
r
m
s
o
f
m
a
s
s
r
A
=-kC
A
F
A0
=90,000 g/min
S
u
b
s
t
i
t
u
t
e
ṁ
i
0
f
o
r
N
i
0
,
&
u
s
e
f
o
r
t
h
e
s
o
l
u
t
i
o
n
t
o
c
a
l
c
u
l
a
t
e
:
Will use Polymath to plot T vs t for CSTR start-up (unsteady-state). Need
equations for dC
A
/dt, dT/dt, and k.
U= 7200
J/min·m
2
·K
A=227.4m
2
C
A0
=180g/
dm
3
=V/
0
T
a
=273K
H
RX
=-2500 J/g
N
i0
=m
i0
V=200 dm
3
C
Ps
=20 J/g
˙
K
0
=500 dm
3
T
0
=313
r
A
=-kC
A
F
A0
=90,000 g/min
T (K)
t (min)
Reaches steady state at ~12 minutes
The
elementary, liquid phase, exothermic reaction A →B
is carried out in a
2 m
3
C
S
T
R
t
h
a
t
i
s
e
q
u
i
p
p
e
d
w
i
t
h
a
h
e
a
t
j
a
c
k
e
t
.
P
u
r
e
A
e
n
t
e
r
s
t
h
e
r
e
a
c
t
o
r
a
t
6
0
m
o
l
/
m
i
n
a
n
d
a
t
e
m
p
e
r
a
t
u
r
e
o
f
3
1
0
K
.
T
h
e
c
o
o
l
a
n
t
i
n
t
h
e
h
e
a
t
j
a
c
k
e
t
i
s
k
e
p
t
a
t
2
8
0
K
.
P
r
o
v
i
d
e
a
l
l
e
q
u
a
t
i
o
n
s
,
a
l
l
c
o
n
s
t
a
n
t
s
,
t
h
e
i
n
i
t
i
a
l
t
i
m
e
,
a
n
d
t
h
e
f
i
n
a
l
t
i
m
e
t
h
a
t
m
u
s
t
b
e
e
n
t
e
r
e
d
i
n
t
o
P
o
l
y
m
a
t
h
i
n
o
r
d
e
r
t
o
p
l
o
t
t
e
m
p
e
r
a
t
u
r
e
v
s
t
i
m
e
f
o
r
t
h
e
f
i
r
s
t
2
0
m
i
n
o
f
r
e
a
c
t
o
r
s
t
a
r
t
-
u
p
.
Δ
H
R
X
(
T
R
)
=
-
1
0
,
0
0
0
c
a
l
/
m
o
l
C
P
A
=
C
P
S
=
1
5
c
a
l
/
m
o
l
·
K
C
p
B
=
1
5
c
a
l
/
m
o
l
·
K
Ẇ
S
=
0
E = 20,000 cal/mol
k = 1 min
-1
at 400 K
UA
=
3200 cal/min•K
0
=
300 L/min
Need equations for how T changes with time, C
A
changes with time, & k changes with T.
C
o
m
b
i
n
e
w
i
t
h
E
B
:
The
elementary, liquid phase, exothermic reaction A →B
is carried out in a
2 m
3
C
S
T
R
t
h
a
t
i
s
e
q
u
i
p
p
e
d
w
i
t
h
a
h
e
a
t
j
a
c
k
e
t
.
P
u
r
e
A
e
n
t
e
r
s
t
h
e
r
e
a
c
t
o
r
a
t
6
0
m
o
l
/
m
i
n
a
n
d
a
t
e
m
p
e
r
a
t
u
r
e
o
f
3
1
0
K
.
T
h
e
c
o
o
l
a
n
t
i
n
t
h
e
h
e
a
t
j
a
c
k
e
t
i
s
k
e
p
t
a
t
2
8
0
K
.
P
r
o
v
i
d
e
a
l
l
e
q
u
a
t
i
o
n
s
,
a
l
l
c
o
n
s
t
a
n
t
s
,
t
h
e
i
n
i
t
i
a
l
t
i
m
e
,
a
n
d
t
h
e
f
i
n
a
l
t
i
m
e
t
h
a
t
m
u
s
t
b
e
e
n
t
e
r
e
d
i
n
t
o
P
o
l
y
m
a
t
h
i
n
o
r
d
e
r
t
o
p
l
o
t
t
e
m
p
e
r
a
t
u
r
e
v
s
t
i
m
e
f
o
r
t
h
e
f
i
r
s
t
2
0
m
i
n
o
f
r
e
a
c
t
o
r
s
t
a
r
t
-
u
p
.
Δ
H
R
X
(
T
R
)
=
-
1
0
,
0
0
0
c
a
l
/
m
o
l
C
P
A
=
C
P
S
=
1
5
c
a
l
/
m
o
l
·
K
C
p
B
=
1
5
c
a
l
/
m
o
l
·
K
Ẇ
S
=
0
E = 20,000 cal/mol
k = 1 min
-1
at 400 K
UA
=
3200 cal/min•K
0
=
300 L/min
Need equations for how T changes with time, C
A
changes with time, & k changes with T.
U
s
e
t
h
e
m
a
s
s
b
a
l
a
n
c
e
t
o
g
e
t
e
q
f
o
r
C
A
(
t
)
This review delves into the concept of multiple steady states in Continuous Stirred Tank Reactors (CSTRs). Through a detailed analysis of mass and energy balances, intersections of temperature and conversion points are identified as steady states. The presentation discusses the implications of varying conditions on reactor stability and provides insights on reactor design. Each intersection represents a unique operating condition with potential implications for reaction kinetics and heat transfer.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
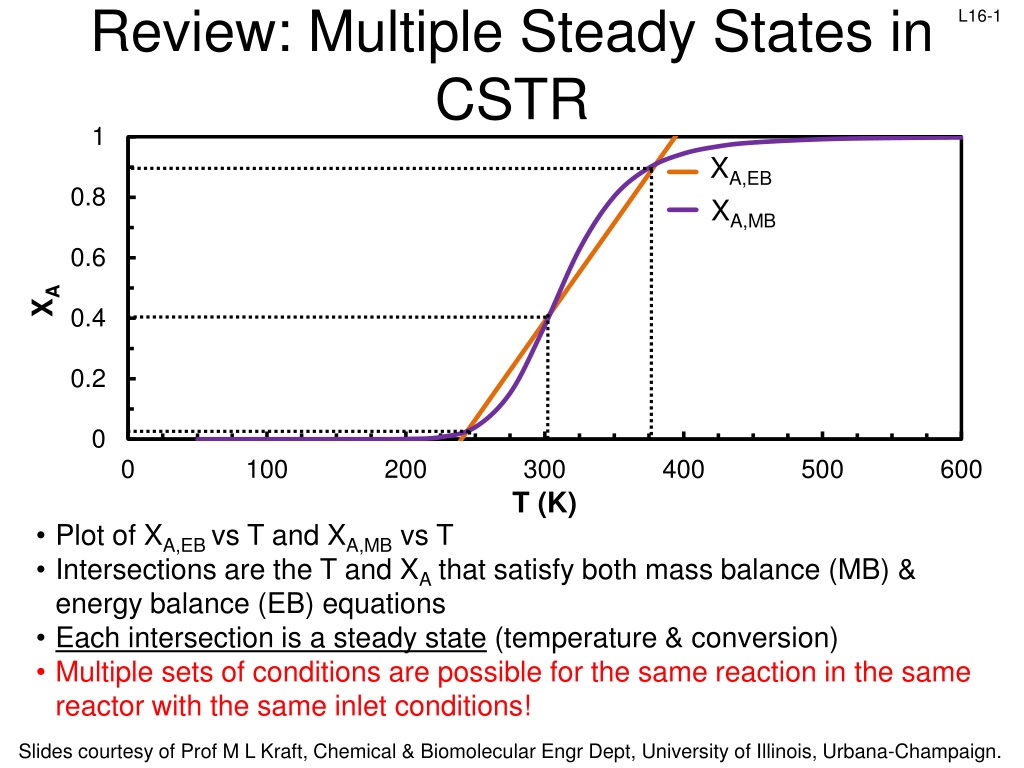
Review: Multiple Steady States in CSTR 1 L16-1 XA,EB XA,MB 0.8 0.6 XA 0.4 0.2 0 0 100 200 300 T (K) 400 500 600 Plot of XA,EB vs T and XA,MB vs T Intersections are the T and XA that satisfy both mass balance (MB) & energy balance (EB) equations Each intersection is a steady state (temperature & conversion) Multiple sets of conditions are possible for the same reaction in the same reactor with the same inlet conditions! Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-2 Review: Heat Removal Term R(T) & T0 Heat removed: R(T) Heat generated G(T) + T 1 T = a 0 UA C F = T p0 A0 r V F c ) + ( A + = C 1 T T H p0 C RX A0 R(T) line has slope of CP0(1+ ) = R(T) = 0 R(T) Increase For Ta < T0 Increase T0 Ta T0 T When increases from lowering FA0 or increasing heat exchange, slope and x-intercept moves Ta<T0: x-intercept shifts left as Ta>T0: x-intercept shifts right as =0, then TC=T0 = , then TC=Ta T When T0 increases, slope stays same & line shifts to right Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-3 Review: CSTR Stability + T 1 T G(T) > R(T) T rises to T=SS3 = UA C F G(T) a 0 p0 A0 = T c + R(T) 3 R(T) > G(T) R(T) > G(T) T falls to T=SS1 T falls to T=SS3 G(T) > R(T) T rises to T=SS1 2 Heat generated G(T) Heat removed: R(T) r V F ) ( A + = C 1 T T H 1 p0 C RX A0 T Magnitude of G(T) to R(T) curve determines if reactor T will rise or fall G(T) = R(T) intersection, equal rate of heat generation & removal, no change in T G(T) > R(T) (G(T) line above R(T) on graph): rate of heat generation > heat removal, so reactor heats up until a steady state is reached R(T) > G(T) (R(T) line above G(T) on graph): rate of heat generation < heat removal, so reactor cools off until a steady state is reached Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
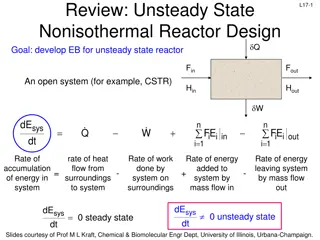
L16: Unsteady State Nonisothermal Reactor Design Goal: develop EB for unsteady state reactor L16-4 Q Fin Fout An open system (for example, CSTR) Hin Hout W dE n n sys dt = + Q W i i in FE i i out FE i 1 = i 1 = Rate of accumulation of energy in system rate of heat flow from surroundings to system Rate of work done by system on surroundings Rate of energy added to system by mass flow in Rate of energy leaving system by mass flow out = - + - dE dE sys dt sys dt = 0 steady state 0 unsteady state Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-5 Change in System Energy with Time n sy s d Q W dt = E n = + i i in FE i i o FE ut i 1 = i 1 n Energy of system is the sum of products of each species specific energy Ei & the moles of each species: = E N E sys i i i 1 = n ( ) ( ) = = E N H PV E U & U H PV so: Differentiate wrt time sys i i i i i i i i = i 1 d E d E n n n d H d N d dt n d dt sy s sys dt i i ( ) = + N H P N V = N H PV i i i i i i i dt dt dt i 1 = i 1 = i 1 = = i 1 Total V d E n n d H d N d d s s y dt For well-mixed reactor with constant PV- variation i i = + N H P V i i dt dt t = i 1 = i 1 0 n n n n d H dt d N dt i i + = + Q W i i FH i i FH N H S i i i 1 = i 1 = i 1 = i 1 = in o u t Total Energy Balance for unsteady state, constant PV Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-6 Well-Mixed Reactors, Constant PV Total Energy Balance for unsteady state n n n n dH dt dN dt d dt i i + = + Q W i i FH i i FH N H PV = 0 S i i i 1 = i 1 = i 1 = i 1 = in out Special case: well-mixed reactors (e.g., batch, CSTR or semibatch) with constant PV- variation in total P or V can be neglected n n n n dH dt dN dt i i + = + Q W i i FH i i FH N H S i i = i 1 = i 1 = i 1 = i 1 in ou t Total Energy Balance for unsteady state, constant PV T dH d dH d dT d ( ) i i = + = E valuate recalling that H H T C dT s o C i RX R pi pi t t t TR n n n n dN dt dT dt i + = + Q W i i FH i i FH N C H S i pi i = i 1 = i 1 = i 1 = i 1 in ou t Need to put dNi/dt into terms that can be measured Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-7 EB for Well-Mixed Reactors, PV=0 n n S i i i i i 1 i 1 in ou = = From the mass balance: In Out - + Gen Accumulation = n n d N dT dt i + = + Q W FH FH N C H i pi i dt i 1 = i 1 = t N d n d dN dt i ( ) i = F F r V = + Substitute F F r V i0 i i A i0 i i A t n n n dT dt n ( ) + = + Q W i i FH i i FH N C H F F r V S i pi i i 0 i i A i 1 = i 1 = = i 1 = i 1 dT dt in ou n t n n n n ( ) + = + + r V Q W i0 i0 F H i i FH N C HF HF i i H S i p i i i0 i i A i 1 = i 1 = = i 1 = i 1 = i 1 = i 1 Add FiHi to both sides of equation: Q W n n n n dT dt ( ) + = + + r V i0 i0 F H N C HF i i H S i pi i i0 A = = i 1 = = i 1 i 1 i 1 Substitute iHi = H RX(T): H RX(T) n n n dT dt ( )( T ) + = + + r V Q W i0 i0 F H N C HF H S i pi i i0 RX A i 1 = = i 1 = i 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-8 Simplified EB for Well-Mixed Reactors n n n dT dt ( )( T ) + = + + r V Q W i0 i0 F H i pi NC HF H Solve for dT/dt: S i i0 RX A i 1 = i 1 = i 1 = Bring Fi0Hi and H RX(T) terms to other side of equation: n n S i0 i0 i 1 i 1 = = n dT dt ( )( T ) + r V = Q W F H HF H i pi NC i i0 RX A i 1 = Factor Fi0Hi0 and Fi0Hi terms and divide by NiCpi : n ( ) ( )( T r V ) + Q W F H H H Energy balance for unsteady state reactor with phase change: S i0 i i0 RX A dT dt i 1 = = n i pi NC i 1 = n ( ) ( )( T r V ) + Q W i0 pi F C T T H Energy balance for unsteady state reactor without phase change: S i0 RX A dT dt i 1 = = n i pi NC i 1 = Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-9 Unsteady State EB, Liquid-Phase Rxns ( = n i pi i 1 n ) ( )( T r V ) + Q W F C T T H i 1 S i0 pi i0 RX A d T = dt NC = For liquid-phase reactions, often Cp = iCpi is so small it can be neglected When Cp can be neglected, then: = = i pi A0 ps ps i pi i 1 If the feed is well-mixed, it is convenient to use: = i0 pi F C F n NC N C where C C is the heat capacity of the sol ution = C A0 ps Plug these equations and Ti0 = T0 into the EB gives: ( ) ( )( T ) + Q W F C T N T C H r V dT dt S A 0 p s i0 R X A = A0 p s This equation for the EB is simultaneously solved with the mass balance (design eq) for unsteady state, nonisothermal reactor design Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-10 Nonisothermal Batch Reactor Design ( S i0 pi i0 i 1 n i pi i 1 = n ) ( )( T r V ) + 0 Q W F C T T H RX A dT dt = = NC ( )( T r V ) + n Q W H No flow, so: d T t S RX A = d N C i pi = i 1 ( N N Put the energy balance in terms of XA: ) i0 = + = i & C = N N X where C i A0 i i A i p i P A 0 ( )( T r V ) + Q W H dT d S RX A = n t + N C C X A0 i p i p A = i 1 Solve with the batch reactor design equation using an ODE solver (Polymath) dX N dt A = r V A0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Adiabatic Nonisothermal Batch Reactor Design Q W H + + In the case of no stirring work and adiabatic operation, ( )( ) = + i 1 ( )( R X T H Rearrange: L16-11 0 0 ( )( T r V ) dT dt S RX A = n N i pi C C X A0 p A i 1 = = W =0 & Q 0 S H T r V dT dt ( )( + ps C ) Substitute: RX A H T r V C X dT dt RX A = n = i pi C C N N i pi C C X ps A0 p A A0 p A = dT d ) = + r V N C C X A A0 p S p A t dX dt ( ) T ( ) ( ) A = + = H H T C T R T an d -N r V Substitute: R X RX R p A 0 A dX dt dX dT d ( ) ( ) A + = + H T C T T N N C C X RX R p R A 0 A0 pS p A t dT dt ( ) ( ) A + = + H T C T T C C X RX R p R pS p A dt Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
dX dt dT dt L16-12 Solve for how XA changes with T ( ) ( ) A + = + H T C T T C C X RX R p R pS p A ( ) ( ) = + + H T C T T dX C C X d T RX R p R A pS p A Get like terms together: XA T + dX dT A C X = 0 ( ) ( ) + C H T C T T = pS p A X 0 T RX R p R A0 Integrate & solve for XA: ( ) ) ( ( ) C T T C T T p T 0 p 0 S S = = X X ( ) A A ( ) T ( ) H + H C T T RX RX R p R Solving for T: ( ) C ( ) H T X H T X RX 0 A RX 0 A = + = + T T T T 0 0 n + C X ps A p + i p C X C A p i = i 1 Heat capacity of soln (calculate Cps if not given) Solve with the batch reactor design equation using an ODE solver (Polymath) XA A0 t N = dX r V A A 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-13 A 1st order, liquid-phase, exothermic reaction A B is run in a batch reactor. The reactor is well-insulated, so no heat is lost to the surroundings. To control the temperature, an inert liquid C is added to the reaction. The flow rate of C is adjusted to keep T constant at 100 F. What is the flow rate of C after 2h? TC0 = 80 F V0= 50 ft3 H RX=-25000 Btu/lb mol k(100 F)= 1.2 x 10-4 s-1 Cp, (all components)= 0.5 Btu/lb mol F CA0= 0.5 lb mol/ft3 1. Solve design eq for comp as function of t 2. Solve EB for FC0 using that info & T=100 F This is essentially a semi-batch reactor since only C is fed into the reactor dN V dt the calculation because V depends on t dX d A t A = N r V Design eq: Note, using would complicate =A r A0 A Rate eq: -rA = kCA dN d dN dt A t N A = = kC V k N Rearrange and integrate for NA Combine: A A t N N dN N A A A = = N N exp kt ln kt = kdt A A0 A0 A N 0 A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-14 A 1st order, liquid-phase, exothermic reaction A B is run in a batch reactor. The reactor is well-insulated, so no heat is lost to the surroundings. To control the temperature, an inert liquid C is added to the reaction. The flow rate of C is adjusted to keep T constant at 100 F. What is the flow rate of C after 2h? Use EB to find how the flow rate of C depends on the rxn (solve EB for FC0) n S i0 pi i 1 n dt NC 0 0 0 ( ) ( )( T r V ) + Q W F C T T H i0 RX A dT = = i pi = i 1 n n ( ) ( )( T r ) ( ) ( )( T r V ) = F C T T H V = + 0 i0 pi F C T T H i0 pi i0 RX A i0 RX A = i 1 C i 1 = ( ) ( )( T r ) = C0 F T T H V C is the only species that flows, so: pC = A N i0 R X A where N ex p kt rAV = -kCAV = -kNA A0 ( )( ) ( ) kt = ( )( C C0 F C T T H T k N e pC i0 RX A0 ) kt kN H T e RX A0 T Isolate FC0: = C0 F ( ) T pC i0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-15 A 1st order, liquid-phase, exothermic reaction A B is run in a batch reactor. The reactor is well-insulated, so no heat is lost to the surroundings. To control the temperature, an inert liquid C is added to the reaction. The flow rate of C is adjusted to keep T constant at 100 F. What is the flow rate of C after 2h? TC0 = 80 F V0= 50 ft3 H RX=-25000 Btu/lb mol k(100 F)= 1.2 x 10-4 s-1 Cp, (all components)= 0.5 Btu/lb mol F CA0= 0.5 lb mol/ft3 ( )( C ) kt ( ) lb mol ft H T k N e 3 R X A 0 = = = N C V 0.5 50ft 25 lb mol = C0 F A0 A0 0 3 ( ) T T pC i0 At 2h (7200s): ) ( 4 1 1.2 1 0 s 7200s Btu m ( ) 4 1 25,000lb 1.2 1 0 s 25 lb mo l e ol = F C 0 ( ) Bt u 0.5lb m 10 0 F 80 F ol F lb mol s = C0 F 3.16 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-16 Instead of feeding coolant to the reactor, a solvent with a low boiling point is added (component D). The solvent has a heat of vaporization of 1000 Btu/lb mol, and initially 25 lb mol of A are placed in the tank. The reactor is well- insulated. What is the rate of solvent evaporation after 2 h if T is constant at 100 F? Still a semibatch reactor, where D is removed from the reactor Use EB that accounts for a phase change: n S i0 i0 i i 1 n i pi i 1 = Additional info: k(100 F)= 1.2 x 10-4 s-1 H RX=-25000 Btu/lb mol 0 0 ( ) ( )( T r V ) + Q W F H H H Q =0 S=0 RX A dT dt = = NC 0 Clicker Question: Does dT/dt = 0? a) Yes b) No Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-17 Instead of feeding coolant to the reactor, a solvent with a low boiling point is added (component D). The solvent has a heat of vaporization of 1000 Btu/lb mol, and initially 25 lb mol of A are placed in the tank. What is the rate of solvent evaporation after 2 h? Additional info: k(100 F)= 1.2 x 10-4 s-1 H RX=-25000 Btu/lb mol Still a semibatch reactor, where D is removed from the reactor Use EB that accounts for a phase change: n S i0 i0 i 1 n dt 0 0 0 ( ) ( )( T r V ) + Q W F H H H Q =0 S=0 dT/dt = 0 i RX A dT = = i pi NC i 1 = n D is the only species that flows , and rAV = -kNA0(exp[-kt]), so: ) = D0 F Hi0-Hi = heat of vap ( ) ( )( T r ) = F H H H V i0 i0 i RX A = i 1 ( )( ( H ) k t ( )( H T k N e R X A0 ( ) kt = D0 F H H H T k N e i0 i R X A 0 ) H i0 i Btu lbmol 0.00012 s ( ) 0.00012 s 7200s lb mol s ( ) 25,000 25 lb mo l e = D0 F 0.0316 = D0 F 1000Bt u lb mol Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
A liquid phase exothermic reaction A B is carried out at 358K in a 0.2 m3 CSTR. The coolant temperature is 273K and the heat transfer coefficient (U) is 7200 J/min m2 K. What is the heat exchange area required for steady state operation? Using this heat exchange area, plot T vs t for reactor start-up. CPA =CPS=20 J/g K S=0 CA0= 180 g/dm3 0= 500 dm3/min = 900 g/dm3 H RX(T) = -2500 J/g a) Heat exchange area for steady state operation: L16-18 T0= 313 K E=94852 J/mol Kk(313K)= 1.1 min-1 n ( ) ( )( T r V ) + Q W i0 pi F C T T H SS operation means that T is constant, so: S i0 RX A dT dt i 1 = = = 0 n i pi NC i 1 = n ( ) ( )( T ) = Q W F C T T H r V S i0 pi i0 RX A = i 1 Q =UA(Ta-T), S=0, and A is only species that flows ( ) a UA T T Plug in rA = -kCA and solve for A ( ) a U T T A ( ) ( )( T r ) = F C T T H V A0 pA A0 RX A ( ) ( )( T ) = F C T T H kC V A0 ( )( T pA A0 RX A ( ) ) + H kC V U T F T C T T RX A A0 pA A0 = A ( ) a Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
A liquid phase exothermic reaction A B is carried out at 358K in a 0.2 m3 CSTR. The coolant temperature is 273K and the heat transfer coefficient (U) is 7200 J/min m2 K. What is the heat exchange area required for steady state operation? Using this heat exchange area, plot T vs t for reactor start-up. CPA =CPS=20 J/g K S=0 CA0= 180 g/dm3 0= 500 dm3/min = 900 g/dm3 H RX(T) = -2500 J/g Use material balance to determine steady state value of CA L16-19 T0= 313 K E=94852 J/mol Kk(313K)= 1.1 min-1 + = A0 0 A 0 = A0 0 = A 0 + F F Ar V 0 C C k C V 0 C C kC V A A0 A A A0 0 C 1.1 min 94852J mol 8.314J mol K 313 1 1 =107.4 min ( ) ( ) = k 358K = exp C k 358K A 358 + k V 0 ( ) 3 3 180 g dm 500dm min 3 = = C C 4.1g dm ( ) A A 3 1 3 + 500d m m n i 107.4min 2 00dm ( ) ( )( T ) + H k C V T F T C T T R X A A0 pA A0 = Solve EB for A: A ( ) U a 3 3 = g m dm 1000dm m 3 3 = = F 180 500m 90000g m n i =0.2 V m 200dm A0 3 3 n i d Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
A liquid phase exothermic reaction A B is carried out at 358K in a 0.2 m3 CSTR. The coolant temperature is 273K and the heat transfer coefficient (U) is 7200 J/min m2 K. What is the heat exchange area required for steady state operation? Using this heat exchange area, plot T vs t for reactor start-up. CPA =CPS=20 J/g K S=0 CA0= 180 g/dm3 0= 500 dm3/min = 900 g/dm3 H RX(T) = -2500 J/g Solve for heat exchange area at SS: ( )( = U T L16-20 T0= 313 K E=94852 J/mol Kk(313K)= 1.1 min-1 ( ) ) + H T k C V F T C T T RX A A 0 p A A 0 A ( ) a FA0=90,000 g/min k= 107.4 min-1 CA= 4.1 g/dm3 CPA =20 J/g K U= 7200 J/min m2 K TA0= 313 K V=200 dm3 H RX(T) = -2500 J/g T= 358K Ta=273K J 10 m 7.4 in g m g J ( ) 3 + 2500g 4.1 200dm 90000m 20g 358 K 313 K 3 i n K d = A J ( ) 7 200 2 73K 358K 2 min m K A=227.4 m2 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-21 Will use Polymath to plot T vs t for CSTR start-up (unsteady-state). Need equations for dCA/dt, dT/dt, and k. dN F F r V dt ( ) ( ) a A0 pA i0 n i0 ps i 1 = CPs is in terms of mass (J/g K), so FA0 & Ni0 must also be in terms of mass FA0=90,000 g/min Substitute i0 for Ni0, & use for the solution to calculate: = dm Amount of gas leaving reactor (L7) C dC dt C A A0 A A = + = + Mass balance: r A0 A A A ( ) + UA T T F C T T H r V dT dt RX A = N C g 3 = m 200d m 9 0 0 = m 180,000g m V rA=-kCA i0 i0 i0 3 1.1 min 94852J mol 8.314J mol K 313 1 1 T 1.1 min 11408.7 K 1 1 T k= exp k= exp 313 =V/ 0 Ta=273K 0=500 dm3 T0=313 U= 7200 J/min m2 K HRX=-2500 J/g Ni0=mi0 V=200 dm3 CPs=20 J/g K A=227.4m2 CA0=180g/dm3 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-22 Will use Polymath to plot T vs t for CSTR start-up (unsteady-state). Need equations for dCA/dt, dT/dt, and k. C dC C r dt ( ) ( ) a A0 pA i0 n i0 ps i 1 = U= 7200 J/min m2 K A=227.4m2 CA0=180g/dm3 HRX=-2500 J/g Ni0=mi0 V=200 dm3 CPs=20 J/g K 1.1 min 11408.7 K 1 1 T A0 A A k= exp rA=-kCA = + A 313 ( ) + UA T T F C T T H r V dT dt RX A = = m 180,000g i0 N C FA0=90,000 g/min =V/ 0 Ta=273K 0=500 dm3 T0=313 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-23 T (K) t (min) Reaches steady state at ~12 minutes Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-24 The elementary, liquid phase, exothermic reaction A B is carried out in a 2 m3 CSTR that is equipped with a heat jacket. Pure A enters the reactor at 60 mol/min and a temperature of 310K. The coolant in the heat jacket is kept at 280 K. Provide all equations, all constants, the initial time, and the final time that must be entered into Polymath in order to plot temperature vs time for the first 20 min of reactor start-up. HRX(TR) = -10,000 cal/mol CPA = CPS =15 cal/mol K E = 20,000 cal/mol k = 1 min-1 at 400 K Need equations for how T changes with time, CA changes with time, & k changes with T. ( ) pi R i S i0 i 1 dT dt CpB=15 cal/mol K S=0 0= 300 L/min UA= 3200 cal/min K n ( )( T ) + Q ) W F C T T H r V ( 0 X A = = W 0 Q UA T -T = = a S n N C i pi = ( i 1 T b a cal ( ) T ( ) ) = + H H T C T = = 15 15 = C C C C 0 p P PB PA RX RX R P R mol K cal ( ) T ( ) T ( ) = H 10,000mol = + H H T 0 RX RX RX R n n n = N C ( N C = F C F C = = + F ( 0 F C F C F C i pi A0 ps i0 pi A0 p,A B0 i0 pi A 0 p,A B0 p, B = i 1 i 1 = = i 1 ) ) ( ) + UA Ta -T F C T T rAV H T dT dt RX R A 0 p,A i 0 Combine with EB: = N C A0 p s Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L16-25 The elementary, liquid phase, exothermic reaction A B is carried out in a 2 m3 CSTR that is equipped with a heat jacket. Pure A enters the reactor at 60 mol/min and a temperature of 310K. The coolant in the heat jacket is kept at 280 K. Provide all equations, all constants, the initial time, and the final time that must be entered into Polymath in order to plot temperature vs time for the first 20 min of reactor start-up. HRX(TR) = -10,000 cal/mol CPA = CPS =15 cal/mol K E = 20,000 cal/mol k = 1 min-1 at 400 K Need equations for how T changes with time, CA changes with time, & k changes with T. ( ) RX H T 10,000mol dT dt UA 3200 = 280 = = i0 T 310 = = A0 F 60 = CpB=15 cal/mol K S=0 0= 300 L/min UA= 3200 cal/min K ) ( ( ) cal ( ) + UA Ta -T F C T T rAV H T = RX R A 0 p,A i 0 = N C a T A0 p s 20,000 1.987 1 1 T ( ) 1 exp C 15 Ar kC = k PA A 400 = F V 300 N ( ) = A 0 0 N = A 0 F = = 3 3 V 2m 1000L 1 m V 2 00 0 A0 A0 0 V 0 = C 15 0 PS ( ) t 0 ( ) f = = t 20 Use the mass balance to get eq for CA(t) C d C C dN d d N dt = A0 k C A A = C C k C V A = F F r V A A = A0 0 A 0 A d t V A0 A A t C F = A0 A 0 0 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
