Hidden Markov
A detailed overview of Hidden Markov Model (HMM) and the Viterbi Algorithm. Covers notations, components, scenarios like the Occasionally Dishonest Casino Problem, and important questions addressed by the Forward and Viterbi algorithms. Learn about the most likely path in HMMs and how to find it using the Viterbi Algorithm.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Hidden Markov Model-Viterbi Algorithm Lecture 10 Department of CSE, DIU
CONTENTS 1. Hidden Markov Model - Notations 1. Hidden Markov Model - Viterbi Algorithm
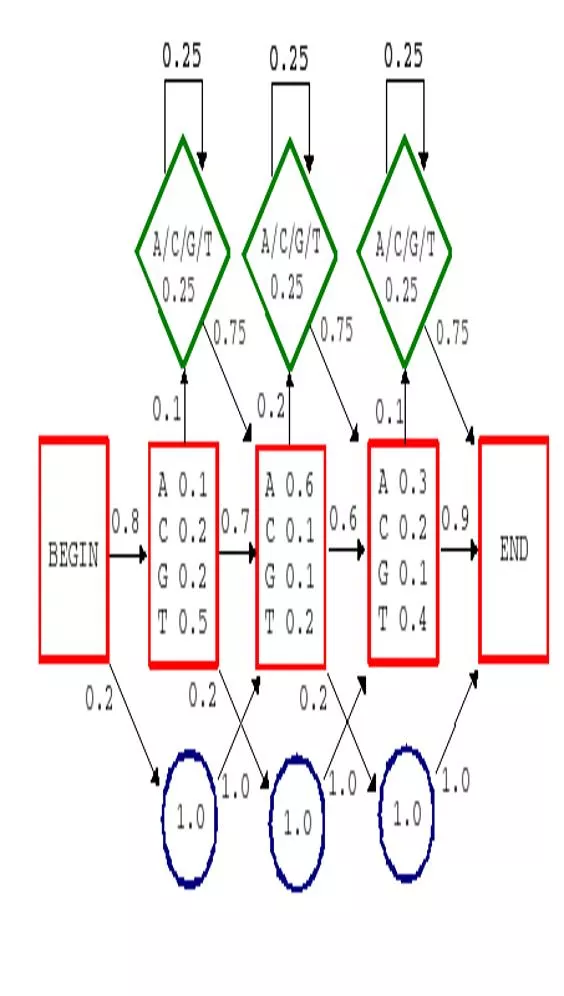
Hidden Markov Model (HMM) Components: Observed variables Emitted symbols Hidden variables Relationships between them Represented by a graph with transition probabilities Goal: Find the most likely explanation for the observed variables
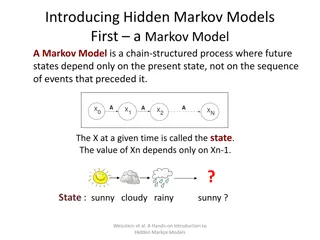
Hidden Markov Model: Notations States are decoupled from symbols x is the sequence of symbols emitted by model xiis the symbol emitted at time i A path, , is a sequence of states The i-th state in is i akr is the probability of making a transition from state k to state r: akr=Pr( i=r| i 1=k) ek(b) is the probability that symbol b is emitted when in state k ek(b) = Pr(xi= b | i= k)
Scenario: The Occasionally Dishonest Casino Problem A casino uses a fair die most of the time, but occasionally switches to a loaded one Fair die: Prob(1) = Prob(2) = . . . = Prob(6) = 1/6 Loaded die: Prob(1) = Prob(2) = . . . = Prob(5) = 1/10, Prob(6) = These are the emission probabilities Transition probabilities Prob(Fair Loaded) = 0.01 Prob(Loaded Fair) = 0.2 Transitions between states obey a Markov process
An HMM for Occasionally Dishonest Casino akl 0.99 0.80 0.01 1: 2: 1/6 1/6 1: 1/10 2: 1/10 3: 1/10 4: 1/10 5: 1/10 6: 1/2 3: 1/6 4: 1/6 5: 1/6 6: 1/6 0.2 ek(b) Fair Loaded
Important Questions How likely is a given sequence? the Forward algorithm What is the most probable path for generating a given sequence? the Viterbi algorithm
The Most Probable Path The most likely path *satisfies *= argmax Pr(x, ) To find *, consider all possible ways the last symbol of x could have been emitted Let vk(i) = Prob. of path 1,L , i mostlikely to emit x1,K ,xi such that i= k Then v (i) = e (x )max( v (i 1)a ) k k i r rk r
The Viterbi Algorithm (i = 0) Initialization: v0(0) =1, vk(0) = 0for k 0 Recursion: (i = 1, . . . , L): For each state k vk(i) = ek(xi)max(vr(i 1)ark) r Termination: Pr(x, ) = max(v (L)a ) k * k0 k To find *, use trace-back, as in dynamic programming
Outcome = 6,2,6 Static Probability is always = 0.5 The Viterbi Algorithm Transition Probability 6 2 6 Fair (1/6)x(1/2) = 1/12 (1/6) x max{(1/12) x 0.99, (1/4) x 0.2} (1/6)x max{0.01375 x 0.99, 0.02 x 0.2} = 0.00226875 = 0.01375 Loaded (1/2) x (1/2) = 1/4 (1/10)x max{(1/12) x 0.01, (1/4) x 0.8} (1/2) x max{0.01375 x 0.01, 0.02 x 0.8} = 0.08 = 0.02 0.80 0.99 1: 1/10 2: 1/10 3: 1/10 4: 1/10 5: 1/10 6: 1/2 0.01 1: 1/6 2: 1/6 3: 1/6 4: 1/6 5: 1/6 6: 1/6 v (i) = e (x )max( v (i 1)a ) k k i r rk r 0.2 Loaded Fair
The Viterbi Algorithm: Example 6 2 6 Fair (1/6)x(1/2) = 1/12 (1/6) x max{(1/12) x 0.99, (1/4) x 0.2} (1/6)x max{0.01375 x 0.99, 0.02 x 0.2} = 0.00226875 = 0.01375 Loaded (1/2) x (1/2) = 1/4 (1/10)x max{(1/12) x 0.01, (1/4) x 0.8} (1/2) x max{0.01375 x 0.01, 0.02 x 0.8} = 0.08 = 0.02 0.80 0.99 1: 1/10 2: 1/10 3: 1/10 4: 1/10 5: 1/10 6: 1/2 0.01 1: 1/6 2: 1/6 3: 1/6 4: 1/6 5: 1/6 6: 1/6 v (i) = e (x )max( v (i 1)a ) k k i r rk r 0.2 Loaded Fair