Profile Hidden Markov Models

Hidden Markov Models (HMMs) and Profile Hidden Markov Models (PHMMs) are powerful machine learning techniques used in various fields such as speech analysis, music search engines, malware detection, and intrusion detection systems. While HMMs have limitations regarding positional information and memory, PHMMs aim to overcome these constraints by defining multiple B matrices for each position in a sequence. In bioinformatics, aligning multiple related sequences and generating a PHMM based on multiple sequence alignment (MSA) are common practices. Training PHMM involves determining MSA, which is challenging, but defining PHMM matrices is relatively easier compared to training HMM. PHMM and HMM training processes are contrasting in terms of complexity and ease of implementation.

• HMM
• PHMM
• Machine Learning
• Bioinformatics
• Sequence Alignment

ozie_67 Follow

Uploaded on Feb 17, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Profile Hidden Markov Models Mark Stamp PHMM 1

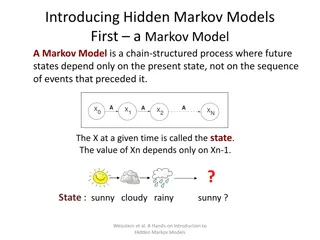
2. Hidden Markov Models Here, we assume you know about HMMs o If not, see A revealing introduction to hidden Markov models Executive summary of HMMs o HMM is a machine learning technique o and a discrete hill climb technique o Train model based on observation sequence o Score any given sequence to determine how closely it matches the model o Efficient algorithms and many useful apps PHMM 2

3. HMM Notation Recall, HMM model denoted = (A,B, ) Observation sequence is O Notation: PHMM 3

4. Hidden Markov Models Among the many uses for HMMs Speech analysis Music search engine Malware detection Intrusion detection systems (IDS) And more all the time PHMM 4

5. Limitations of HMMs Positional information not considered o HMM has no memory beyond previous state o Higher order models have more memory o But no explicit use of positional information With HMM, no insertions or deletions These limitations are serious problems in some applications o In bioinformatics string comparison, sequence alignment is critical o Also, insertions and deletions can occur PHMM 5

6. Profile HMM Profile HMM (PHMM) designed to overcome limitations on previous slide o In some ways, PHMM easier than HMM o In some ways, PHMM more complex The basic idea of PHMM ? o Define multiple B matrices o Almost like having an HMM for each position in sequence PHMM 6

7. PHMM In bioinformatics, begin by aligning multiple related sequences o Multiple sequence alignment (MSA) o Analogous to training phase for HMM Generate PHMM based on MSA o This is easy, once MSA is known o Again, hard part is generating MSA Then can score sequences using PHMM o Use forward algorithm, similar to HMM PHMM 7

8. Training: PHMM vs HMM Training PHMM o Determine MSA challenging o Determine PHMM matrices easy Training HMM o Append training sequences trivial o Determine HMM matrices challenging PHMM and HMM are, in this sense, almost opposites PHMM 8

9. Generic View of PHMM Have delete, insert, and match states o Match states correspond to HMM states Arrows are possible transitions o Each transition has a probability Transition probabilities are A matrix Emission probabilities are B matrices o In PHMM, observations called emissions o Match and insert states have emissions PHMM 9

10. PHMM without Gaps If no gaps, PHMM is simple Illustrate such a PHMM as Here, Mi is ith match state o This diagram neglects the B matrices o Recall, that there is a distinct B matrix for each match state PHMM 10

11. PHMM with Insertions If we also allow for insertions, diagram is of the form Allows for multiple insertions PHMM 11

12. PHMM with Deletions If instead, we allow for deletions, we obtain the following diagram Note that a deletion skips over the corresponding match state PHMM 12

13. Generic View of PHMM Circles are delete states, diamonds are insert states, squares are match states Note the many possible transitions PHMM 13

14. PHMM Notation Notation PHMM 14

15. PHMM Match state probabilities easily determined from MSA aMi,Mi+1 transitions between match states eMi(k) emission probability at match state Many other transition probabilities o For example, aMi,Ii and aMi,Di+1 Emissions at all match & insert states o Remember, emission == observation PHMM 15

16. Multiple Sequence Alignment First we show MSA construction o This is the difficult part o Lots of ways to do this o Best way depends on specific problem Then construct PHMM from MSA o This is the easy part o Standard algorithm to generate PHMM How to score a sequence? o Forward algorithm, similar to HMM PHMM 16

17. MSA How to construct MSA? o Construct pairwise alignments o Combine pairwise alignments into MSA Allow gaps to be inserted o To make better matches Gaps tend to weaken PHMM scoring o So, tradeoff between number of gaps and strength of score PHMM 17

18. Global vs Local Alignment For these pairwise alignment examples o - is gap o | means elements aligned o * for omitted beginning/ending symbols PHMM 18

19. Global vs Local Alignment Global alignment is lossless o But gaps tend to proliferate o And gaps increase when we do MSA o More gaps, more random sequences match o and result is less useful for scoring We usually only consider local alignment o That is, omit ends for better alignment For simplicity, we do global alignment in examples presented here PHMM 19

20. Pairwise Alignment Allow gaps when aligning How to score an alignment? o Based on n x n substitution matrix S o Where n is number of symbols What algorithm(s) to align sequences? o Usually, dynamic programming o Sometimes, HMM is used o Other? Local alignment? Additional issues arise PHMM 20

21. Pairwise Alignment Example Tradeoff: Gaps vs misaligned elements o Depends on matrix S and gap penalty function PHMM 21

22. Substitution Matrix For example, masquerade detection o Detect imposter using computer account Consider 4 different operations o E == send email o G == play games o C == C programming o J == Java programming How similar are these to each other? PHMM 22

23. Substitution Matrix Consider 4 different operations: o E, G, C, J Possible substitution matrix: Diagonal matches o High positive scores Which others most similar? o J and C, so substituting C for J is a high score Game playing/programming, very different o So substituting G for C is a negative score PHMM 23

24. Substitution Matrix Depending on problem, might be easy or very difficult to find useful S matrix Consider masquerade detection based on UNIX commands o Sometimes difficult to say how close 2 commands are Suppose instead, aligning DNA sequences o Biologically valid reasons for S matrix PHMM 24

25. Gap Penalty Generally must allow gaps to be inserted But gaps make alignment more generic o Less useful for scoring, so we penalize gaps How to penalize gaps? Two common ways Linear gap penalty function: g(x) = ax (constant penalty for every gap) Affine gap penalty function g(x) = a + b(x 1) o Gap opening penalty a and constant penalty of b for each extension of existing gap PHMM 25

26. Pairwise Alignment Algorithm We use dynamic programming o Based on S matrix, gap penalty function Notation: PHMM 26

27. Pairwise Alignment DP Initialization: Recursion: where PHMM 27

28. MSA from Pairwise Alignments Given pairwise alignments How to construct MSA? Generally use progressive alignment o Select one pairwise alignment o Select another and combine with first o Continue to add more until all are used Relatively easy (good) Gaps proliferate, and it s unstable (bad) PHMM 28

29. MSA from Pairwise Alignments Lots of ways to improve on generic progressive alignment o Here, we mention one such approach o Not necessarily best or most popular Feng-Dolittle progressive alignment o Compute scores for all pairs of n sequences o Select n-1alignments that a) connect all sequences and b) maximize pairwise scores o Then generate a minimum spanning tree o For MSA, add sequences in the order that they appear in the spanning tree PHMM 29

30. MSA Construction Create pairwise alignments o Generate substitution matrix S o Dynamic program for pairwise alignments Use pairwise alignments to make MSA o Use pairwise alignments to construct spanning tree (e.g., Prim s Algorithm) o Add sequences in spanning tree order (from high score, insert gaps as needed) o Note: gap penalty is used here PHMM 30

31. MSA Example Suppose we have 10 sequences, with the following pairwise alignment scores PHMM 31

32. MSA Example: Spanning Tree Spanning tree based on scores So process pairs in following order: (5,4), (5,8), (8,3), (3,2), (2,7), (2,1), (1,6), (6,10), (10,9) PHMM 32

33. MSA Snapshot Intermediate step and final o Use + for neutral symbol o Then - for gaps in MSA Note increase in gaps PHMM 33

34. PHMM from MSA In PHMM, determine match and insert states & probabilities from MSA Conservative columns are match states o Half or less of symbols are gaps Other columns are insert states o Majority of symbols are gaps Delete states are a separate issue PHMM 34

35. PHMM States from MSA Consider a simpler MSA Columns 1,2,6 are match states 1,2,3, respectively o Since less than half gaps Columns 3,4,5 are combined to form insert state 2 o Since more than half gaps o Match states between insert PHMM 35

36. Probabilities from MSA Emission probabilities o Based on symbol distribution in match and insert states State transition probs o Based on transitions in the MSA PHMM 36

37. Probabilities from MSA Emission probabilities: But 0 probabilities are bad o Model overfits the data o So, use add one rule o Add one to each numerator, add total to denominators PHMM 37

38. Probabilities from MSA More emission probabilities: But 0 probabilities still bad o Model overfits the data o Again, use add one rule o Add one to each numerator, add total to denominators PHMM 38

39. Probabilities from MSA Transition probabilities: We look at some examples o Note that - is delete state First, consider begin state: Again, use add one rule PHMM 39

40. Probabilities from MSA Transition probabilities When no information in MSA, set probs to uniform For example I1 does not appear in MSA, so PHMM 40

41. Probabilities from MSA Transition probabilities, another example What about transitions from state D1? Can only go to M2, so Again, use add one rule: PHMM 41

42. PHMM Emission Probabilities Emission probabilities for the given MSA o Using add-one rule PHMM 42

43. PHMM Transition Probabilities Transition probabilities for the given MSA o Using add-one rule PHMM 43

44. PHMM Summary Construct pairwise alignments o Usually, use dynamic programming Use these to construct MSA o Lots of ways to do this Using MSA, determine probabilities o Emission probabilities o State transition probabilities Then we have trained a PHMM o Now what??? PHMM 44

45. PHMM Scoring Want to score sequences to see how closely they match PHMM How did we score using HMM? o Forward algorithm How to score sequences with PHMM? o Forward algorithm (surprised?) But, algorithm is a little more complex o Due to more complex state transitions PHMM 45

46. Forward Algorithm Notation o Indices i and j are columns in MSA o xi is ith observation (emission) symbol o qxi is distribution of xiin random model o Base case is o is score of x1, ,xiup to state j (note that in PHMM, i and j may not agree) o Some states undefined o Undefined states ignored in calculation PHMM 46

47. Forward Algorithm Compute P(X| ) recursively Note that depends on , and o And corresponding state transition probs PHMM 47

48. PHMM We will see examples of PHMM used in security application later In particular, o Malware detection based on opcodes o Masquerade detection based on UNIX commands o Malware detection based on dynamically extracted API calls PHMM 48

49. References Durbin, et al, Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids L. Huang and M. Stamp, Masquerade detection using profile hidden Markov models, Computers & Security, 30(8):732-747, 2011 S. Attaluri, S. McGhee, and M. Stamp, Profile hidden Markov models for metamorphic virus detection, Journal in Computer Virology, 5(2):151-169, 2009 PHMM 49