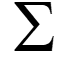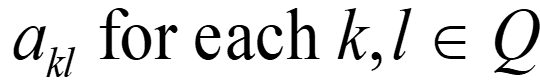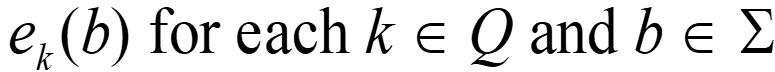Hidden Markov Models
Delve into the intricacies of Hidden Markov Models (HMMs) in the realm of probability theory with topics ranging from model specification to computational problems like determining optimal hidden sequences. Explore how HMMs are utilized in scenarios where transition and emission probabilities are known or unknown, and uncover the methodologies such as the Viterbi algorithm and Baum-Welch algorithm employed to tackle such problems.
Uploaded on Feb 17, 2025 | 0 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Hidden Markov Models Usman Roshan BNFO 601
Hidden Markov Models S Alphabet of symbols: Set of states that emit symbols from the alphabet: Set of probabilities State transition: Emission probabilities: ek(b) for each k Q and b S Q akl for each k,l Q
Loaded die problem S={1,2,3,4,5,6}, Q={F,L} eF(i) =1/6 for all i =1..6 eL(i)=0.1 for all i =1..5 and eL(6) =0.5 aFF=0.95 aFL=0.05 aLL=0.9 aLF=0.1
Loaded die automata aFL F L aFF aLL eF(i) eL(i) aLF
Loaded die problem Consider the following rolls: Observed : Underlying die : FFLLFLLF What is the probability that the underlying path generated the observed sequence? L (X) 21665261 (P) p0=begin pL+1=end P(X,P)= ap0p1 epi(xi) . apipi+1 i=1
HMM computational problems Hidden sequence known Hidden sequence unknown Transition and emission probabilities known Model fully specified Viterbi to determine optimal hidden sequence Transition and emission probabilities unknown Maximum likelihood Expected maximization and also known as Baum-Welch
Probabilities unknown but hidden sequence known Akl: number of transitions from state k to l Ek(b): number of times state k emits symbol b Akl akl= Akq q Q Ek(b) ek(b) = Ek(s) s S
Probabilities known but hidden sequence unknown Problem: Given an HMM and a sequence of rolls, find the most probably underlying generating path. Let be the sequence of rolls. Let VF(i) denote the probability of the most probable path of that ends in state F. (Define VL(i) similarly.) x1x2 xn x1x2 xi
Probabilities known but hidden sequence unknown Initialize: Recurrence: for i=0..n-1 Vbegin(0)=1, VL(0)=0, VF(0)=0 VL(i)aLL VF(i)aFL VB(i)aBL VL(i+1)= eL(xi+1)max VL(i)aLF VF(i)aFF VB(i)aBF VF(i+1)= eF(xi+1)max We do traceback like in Needleman-Wunsch: Remember the array where the max came from
Probabilities and hidden sequence unknown Use Expected-Maximization algorithm (also known as EM algorithm) Very popular and many applications For HMMs also called Baum-Welch algorithm Outline: 1. Start with random assignment to transition and emission probabilities 2. Compute expected transition and emission probabilities using forward and backward procedures. 3. Estimate actual transition and emission probabilities from expected values in previous step 4. Go to step 2 if not converged
Sequence alignment Biological sequence analysis, Durbin et. al., 1998
Alignment HMM Input: seq1 and seq2 Hidden states M: match or mismatch X: gap in aligned seq1 Y: gap in aligned seq2 B: begin Emission probabilities pm: probability of match by M (pm=.6) pmm: probability of mismatch by M (1-pm) pgap: probability of gap by X or Y (equal to 1)
Alignment HMM Transition probabilities MX = MY = delta, MM=1-2delta-tau XX = eta, XM = 1-eta-tau, XY=0 YY = eta, YM = 1-eta-tau, YX=0 BM = 1-2delta-tau, BX=delta, BY=delta
Alignment HMM Viterbi Input are two DNA sequences X and Y of lengths m and n. Assume X (also seq1) is along the rows and Y (also seq2) is along the columns. Define M(i,j) as the probability of the optimal alignment of x1x2...xi and y1y2...yj such that xi is aligned to yj. X(i,j) as the probability of the optimal alignment of x1x2...xi and y1y2...yj such that xi is aligned to a gap. Y(i,j) as the probability of the optimal alignment of c1x2...xi and y1y2...yj such that yj is aligned to a gap. Can you derive dynamic programming recurrence equations for M, X, and Y? What about initialization?
Alignment HMM Viterbi Initialization B[i][j]=0 for 0<=i<=len(seq2), 0<=j<=len(seq1), B[0][[0]=1 M[i][j]=0 for 1<=i<=len(seq2), 1<=j<=len(seq1) X[0][0]=0, X[0][i]=0 for 1<=i<=len(seq1) X[1][0]=pgap*BX*B[0][0] X[i][0]=pgap*XX*X[i-1][0] for 2<=i<len(seq2) Y[0][0]=0, Y[j][0]=0 for 1<=j<=len(seq2) Y[0][1]=pgap*BY*B[0][0] Y[0][i]=pgap*YY*Y[0][i-1] for 2<=i<len(seq1) T[0][j]= L , T[i][0]= U
Alignment HMM Viterbi Recurrence: For 1<=i<=len(seq2), 1<=j<=len(seq1): (MM)M(i -1, j -1) (XM)X(i -1, j -1) (YM)Y(i -1, j -1) (BM)B(i -1, j -1) M(i, j) = pm(or pmm)max (MY)M(i, j -1) (YY)Y(i, j -1) (BY)B(i, j -1) (MX)M(i -1, j) (XX)X(i -1, j) (BX)B(i -1, j) Y(i, j) = pgapmax X(i, j)= pgapmax
Alignment Viterbi HMM Continued from previous slide if(M[i][j] >= X[i][j] AND M[i][j] >= Y[i][j]) T[i][j]= D else if(X[i][j] >= M[i][j] AND X[i][j]] >= Y[i][j]) T[i][j]= U else if(Y[i][j] >= M[i][j] AND Y[i][j] >= X[i][j]) T[i][j]= L
HMM forward probabilities Consider the probability of all alignments of sequences X and Y under a given HMM. Let M(i,j) be the sum of the probabilities of all alignments of X1...i and Y1 j that end in match or mismatch. Then M(i,j) is given by = + (1 2 ) (1 (1 ( 1, 1) 1) 1) M i X i j + ( , ) (or ) ) ( ) ( Y i 1, 1, M i j p p j m mm j We calculate X(i,j) and Y(i,j) in the same way. We call these forward probabilities: f(i,j) = M(i,j)+X(i,j)+Y(i,j)
HMM backward probabilities Similarly we can calculate backward probabilties M (i,j). Define M (i,j) as the sum of probabilities of all alignments of Xi..m and Yj..n such that Xi and and Yj are aligned to each other. The indices i and j start from m and n respectively and decrease (1 2 ) '( , ) (or ) m mm M i j p p = + + + '( 1, 1) 1) 1) + M i X i j + + + (1 ) '( 1, 1, + j (1 ) '( Y i j These are also called backward probabilities. B(i,j)=M (i,j)+X (i,j)+Y (i,j)
Baum Welch How do we calculate expected transition and emission probabilities? Consider the fair-loaded die problem. What is the expected transition of fair (F) to loaded (L)? To answer we have to count the number of times F transitions to L in all possible hidden sequences and multiply each by the probability of the hidden sequence
Baum Welch For example suppose input is 116 There are 8 possible hidden sequences What is the probability of all hidden sequences where F transitions to L between first and second emission What about second and third emission? What about all consecutive positions? What if we have more than one training sequence?
Baum Welch General formula for expected number of transitions from state k to l. General formula for expected number of emissions of b from state k. Equations from Durbin et. al., 1998
Baum Welch 1. Initialize random values for all parameters 2. Calculate forward and backward probabilities 3. Calculate new model parameters 4. Did the probabilities change by more than 0.001? If yes goto step 2. Otherwise stop.
Profile HMMs Used for classifying proteins and RNAs into their families PFAM and RFAM General idea: Create profile of multiple sequence alignments of families Assign protein to family with highest alignment score normalized by length (according to HMM or otherwise)