Graphical Technique for Adding Vectors - Example of Total Displacement Calculation
Example illustrating the graphical technique for adding vectors to determine the total displacement of a person walking three different paths on a flat field. The person walks specific distances in various directions, and the total displacement is calculated using head-to-tail method.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
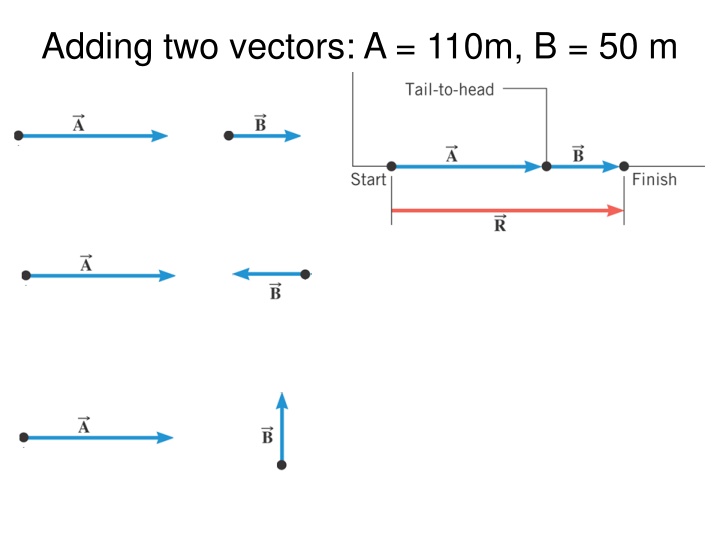
Adding Vectors: Head-to-Tail Method Example 3.1: A Woman Takes a Walk (Page 91, Text) Use the graphical technique for adding vectors to find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction 49.0 north of east. Then, she walks 23.0 m heading 15.0 north of east. Finally, she turns and walks 32.0 m in a direction 68.0 south of east.
Adding Vectors: Head-to-Tail Method Example 3.1: A Woman Takes a Walk (Page 91, Text) Use the graphical technique for adding vectors to find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction 49.0 north of east. Then, she walks 23.0 m heading 15.0 north of east. Finally, she turns and walks 32.0 m in a direction 68.0 south of east.
Adding Vectors: Head-to-Tail Method Example 3.1: A Woman Takes a Walk (Page 91, Text) Use the graphical technique for adding vectors to find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction 49.0 north of east. Then, she walks 23.0 m heading 15.0 north of east. Finally, she turns and walks 32.0 m in a direction 68.0 south of east.
Adding Vectors: Head-to-Tail Method Example 3.1: A Woman Takes a Walk (Page 91, Text) Use the graphical technique for adding vectors to find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction 49.0 north of east. Then, she walks 23.0 m heading 15.0 north of east. Finally, she turns and walks 32.0 m in a direction 68.0 south of east.
Adding Vectors: Head-to-Tail Method Example 3.1: A Woman Takes a Walk (Page 91, Text) Use the graphical technique for adding vectors to find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction 49.0 north of east. Then, she walks 23.0 m heading 15.0 north of east. Finally, she turns and walks 32.0 m in a direction 68.0 south of east.
Adding Vectors: Head-to-Tail Method Example 3.1: A Woman Takes a Walk (Page 91, Text) Use the graphical technique for adding vectors to find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction 49.0 north of east. Then, she walks 23.0 m heading 15.0 north of east. Finally, she turns and walks 32.0 m in a direction 68.0 south of east.
Adding Vectors: Head-to-Tail Method Example 3.1: A Woman Takes a Walk (Page 91, Text) Use the graphical technique for adding vectors to find the total displacement of a person who walks the following three paths (displacements) on a flat field. First, she walks 25.0 m in a direction 49.0 north of east. Then, she walks 23.0 m heading 15.0 north of east. Finally, she turns and walks 32.0 m in a direction 68.0 south of east.
Vector Addition and Subtraction B + A B A A B A B
Addition of Vectors using Vector Components A jogger runs 145 m in a direction 20.0 east of north (displacement vector A) and then 105 m in a direction 35.0 south of east (displacement vector B). Using components, determine the magnitude and direction of the resultant vector C.
Analytical/Component Method Find the resultant and equilibrant of the three vectors in the drawing by means of the component method. The magnitudes of the vectors are A = 250-g, B = 300-g, and C = 260-g.