Control System Synthesis and Compensation Techniques
Explore various chapters discussing topics like direct synthesis, closed-loop transfer functions, PI controllers, time delay compensation, and Smith predictor approach in control systems. Learn about modeling feedback controllers, closed-loop performance, and response specifications.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
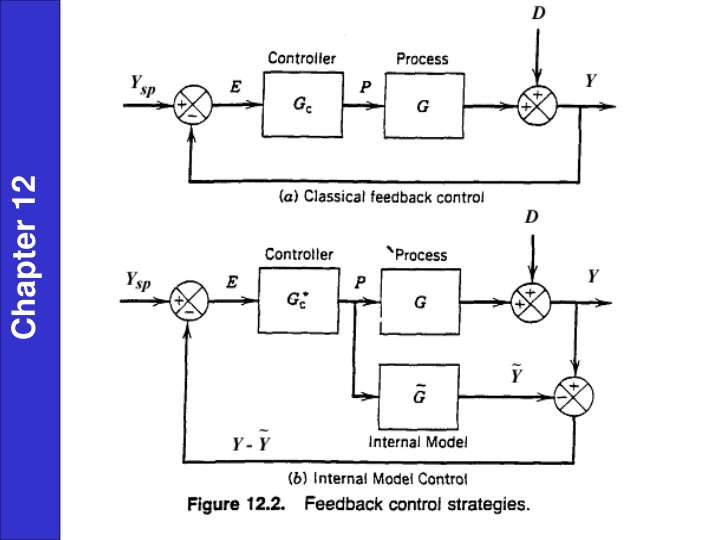
Direct Synthesis G + G Y =1 C ( G includes Gm, Gv) Y G G sp C 1. Specify closed-loop response (transfer function) Chapter 12 Y Y sp d 2. Need process model, (= GPGMGV) G 3. Solve for Gc, Y Y 1 G (12-3b) sp = G d C Y Y 1 sp d
Specify Closed Loop Transfer Function s Y Y e = (12 6) + 1 s sp c d Chapter 12 (first order response, no offset) ( ) = , speedof response = process time delay in G c But other variations of (12-6) can be used (e.g., replace time delay with polynomial approximation) 1 G s 1 If = 0, then (12-3b) yields G = ) (12-5) c c K s +1 K s 1 For G = , G = = + (PI) c s +1 K K s c c c
Derivation of PI Controller for FOPTD Process Consider the standard first-order-plus-time-delay model, s Ke ( ) = (12-10) G s Chapter 12 + s 1 Specify closed-loop response as FOPTD (12-6), but approximate - s e - - s. 1 Substituting and rearranging gives a PI controller, ( ) 1 1/ , c c I G K s = + 1 , c K + with the following controller settings: = = K (12-11) c I
Time Delay Compensation Model-based feedback controller that improves closed-loop performance when time delays are present Chapter 16 Effect of added time delay on PI controller performance for a second order process ( 1 = 3, 2 = 5) shown below
Chapter 16 = = * * s s G G G G + G G e G e Y Y No model error: = + C G = C G ( ) C C 1 * s 1 1 G G e sp C * s G G e G G G G + Y Y = = (16 22) C + C * * 1 1 G G sp C C (sensitive to model errors > +/- 20%)
Direct Synthesis Approach (Smith Predictor) G G Y + 1 Y = = s ( ) C G P G Q s e sp C P Assume time delay between set-point change and controlled variable (same as process time delay, ). = Chapter 16 s G e ) s ( P If P C 1 1 R C = = G then C P G 1 s Pe P R Q 1 C = G From Block Diagram, 1 + s P Pe G C Q = GC Equating... 1 ( P Q )
