Bond Pricing and Yield Calculation Examples

The provided content illustrates calculations for bond pricing and yield in various scenarios. It covers topics such as determining current bond prices based on coupon rates, yield to maturity, and time to maturity. Additionally, it explores scenarios with different bond characteristics like annual payments, semi-annual payments, zero-coupon bonds, and varying coupon rates. Various companies' bonds are analyzed to determine the current bond prices under different conditions.

• Bond Pricing
• Yield Calculation
• Coupon Rate
• Maturity
• Finance

chos102 Follow

Uploaded on Oct 01, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

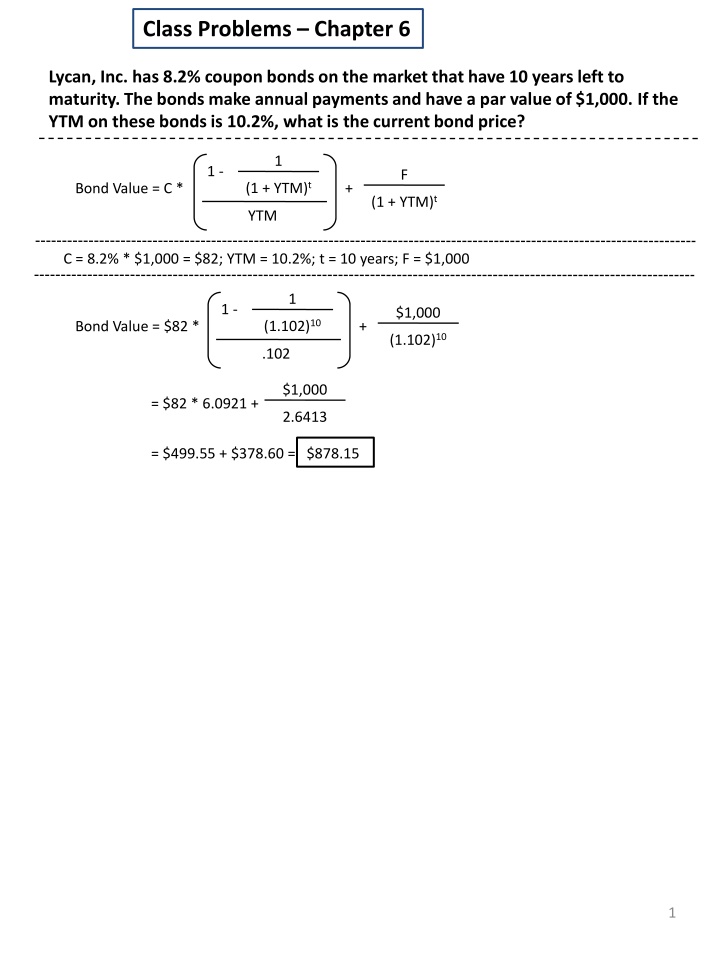
1. Class Problems Chapter 6 Lycan, Inc. has 8.2% coupon bonds on the market that have 10 years left to maturity. The bonds make annual payments and have a par value of $1,000. If the YTM on these bonds is 10.2%, what is the current bond price? 1 1 - F (1 + YTM)t Bond Value = C * + (1 + YTM)t YTM C = 8.2% * $1,000 = $82; YTM = 10.2%; t = 10 years; F = $1,000 1 1 - $1,000 (1.102)10 Bond Value = $82 * + (1.102)10 .102 $1,000 = $82 * 6.0921 + 2.6413 = $499.55 + $378.60 = $878.15 1

2. Volbeat Corporation has bonds on the market making annual payments, with 17 years to maturity, a par value of $1,000, and a price of $956, the bonds yield 9.1%. What must the coupon rate be on the bonds? 1 1 - F (1 + YTM)t Bond Value = C * + (1 + YTM)t YTM Bond Value = $956; YTM = 9.1%; t = 17 years; F = $1,000 1 1 - $1,000 (1.091)17 $956 = C * + (1.091)17 .091 $956 = C * 8.4890 + $227.50 $956 - $227.50 = C * 8.4890 $728.50 / 8.4890 = C $85.82 = 8.58% $85.82 = C Coupon rate = $1,000 Barnes Co. has bonds on the market making annual payments, with 15 years to maturity, a par value of $1,000, and a price of $971, the bonds yield 8.3%. What must the coupon rate be on the bonds? 1 1 - F (1 + YTM)t Bond Value = C * + (1 + YTM)t YTM Bond Value = $971; YTM = 8.3%; t = 15 years; F = $1,000 1 1 - $1,000 (1.083)15 $971 = C * + (1.083)15 .083 $971 = C * 8.4049 + $302.39 $971 - $302.39 = C * 8.4049 $668.61 / 8.4049 = C $79.55 2 = 7.95% $79.55 = C Coupon rate = $1,000

3. Hardwell Inc. issued 14-year bonds one year ago at a coupon rate of 6.9%. The bonds make semi-annual payments. If the YTM of these bonds is 5.5%, what is the current dollar price assuming a $1,000 par value? 1 1 - F (1 + YTM/2)2t + Bond Value = C/2 * (1 + YTM/2)2t (YTM/2) C = 6.9% * $1,000 = $69; YTM = 5.5%; t = 13 years; F = $1,000 1 1 - $1,000 (1 + .055/2)26 Bond Value = $69/2 * + (1 + .055/2)26 (.055/2) $1,000 = $34.50 * 18.4023 + 2.0245 = $634.88 + $493.94 = $1,128.82 3

4. You find a zero coupon bond with a par value of $10,000 and 24 years to maturity. If the YTM on this bond is 4.6%, what is the price of the bond? Assume semi- annual compounding periods. F Bond Value = (1 + YTM/2)2t YTM = 4.6%; t = 24 years; F = $1,000 $10,000 Bond Value = (1 + .046/2)48 = $10,000 / 2.9787 = $3.357.14 If you invest $3,357.14 today, how much will you have in 24 years if you earn 4.6% interest compounded semi-annually? FV = PV * (1 + r)t PV = $3,357.14; r = 2.3% (semi-annual rate); t = 48 (semi-annual period) FV = $3,357.14 * (1 + .023)48 = $10,000.00 Bond Pricing with Semi-Annual Coupons 1 1 - + + C F 2t (1 YTM/2) = = + + Bond Value + + 2t 2 YTM/2 (1 YTM/2) 4

5. PS 1 - Prufrock, Inc. has 7.9% coupon bonds on the market that have 6 years left to maturity. The bonds make annual payments and have a par value of $1,000. If the YTM on these bonds is 9.9%, what is the current bond price? 1 1 - F (1 + YTM)t Bond Value = C * + (1 + YTM)t YTM C = 7.9% * $1,000 = $79; YTM = 9.9%; t = 6 years; F = $1,000 1 1 - $1,000 (1.099)6 Bond Value = $79 * + (1.099)6 .099 $1,000 = $79 * 4.3681 + 1.7619 = $345.08 + $567.56 = $912.64 PS 2 - Guetta Enterprises issued 17-year bonds one year ago at a coupon rate of 7.3%. The bonds make semi-annual payments. If the YTM of these bonds is 5.3%, what is the current dollar price assuming a $1,000 par value? 1 1 - F (1 + YTM/2)2t + Bond Value = C/2 * (1 + YTM/2)2t (YTM/2) C = 7.3% * $1,000 = $73; YTM = 5.3%; t = 16 years; F = $1,000 1 1 - $1,000 (1 + .053/2)32 Bond Value = $73/2 * + (1 + .053/2)32 (.053/2) $1,000 = $36.50 * 21.3953 + 2.3093 = $780.93 + $433.03 = $1,213.96