Algebra 2 Graphing Quadratics Practice
Practice graphing quadratic functions in standard form, identify important parts such as the axis of symmetry, vertex, and intercepts. Solve equations and graph parabolas with step-by-step instructions. Improve your understanding of quadratic functions.
Uploaded on Feb 16, 2025 | 0 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
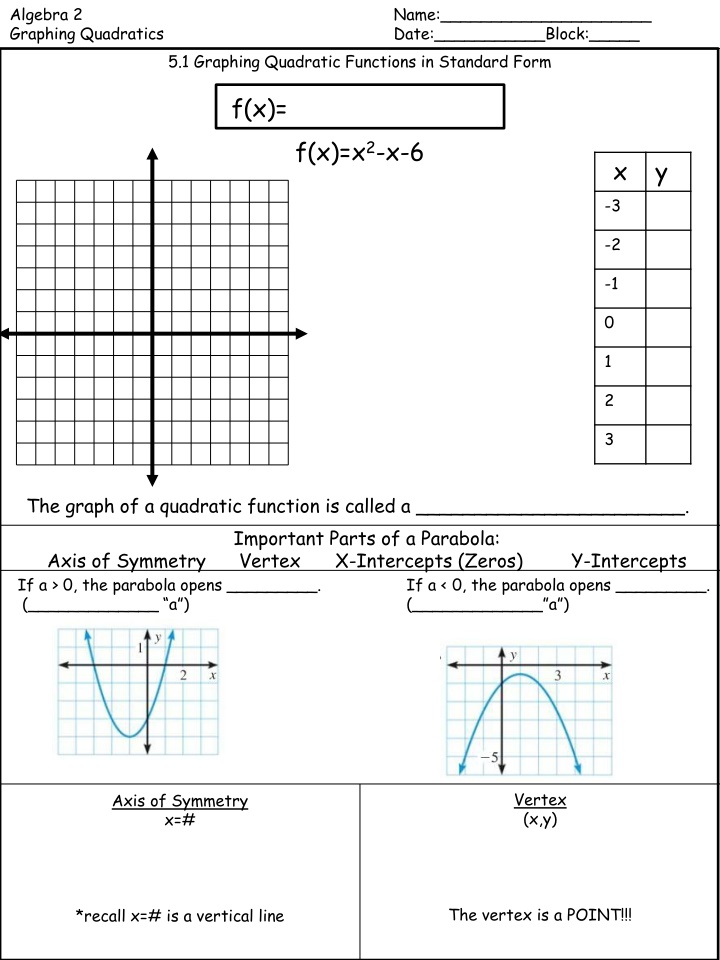
Algebra 2 Graphing Quadratics Name:_____________________ Date:___________Block:_____ 5.1 Graphing Quadratic Functions in Standard Form f(x)= f(x)=x2-x-6 x y -3 -2 -1 0 1 2 3 The graph of a quadratic function is called a _______________________. Important Parts of a Parabola: Axis of Symmetry Vertex X-Intercepts (Zeros) Y-Intercepts If a > 0, the parabola opens _________. (_____________ a ) If a < 0, the parabola opens _________. (_____________ a ) Vertex (x,y) Axis of Symmetry x=# The vertex is a POINT!!! *recall x=# is a vertical line
Examples: For each state the equation of the axis of symmetry and the vertex. y=x2-6x+5 y=-x2-2x+1 Axis of Symmetry: x=___ Vertex:________ Axis of Symmetry: x=___ Vertex:________ Axis of Symmetry: x=___ Vertex:________ Axis of Symmetry: x=___ Vertex:________ Axis of Symmetry: x=___ Vertex:________ To find the x- and y- intercepts of a function . Y-intercept Replace "x" with 0. Solve for "y." X-intercept Replace y" with 0. Solve for x." ** The y-intercept will always be the ____ value Practice: Identify the x and y intercepts for each.
Directions: For each quadratic identify the axis of symmetry, vertex, x- and y-intercepts. Graph the parabola using the information. Show all work. 2) 1) Axis: ____________ x-int: ____________ Vertex: ________ y-int: _________ Axis: x = ____ x-int: (___, 0) & (___, 0) y-int: (0, ___) Vertex: (___, ___) 3) 4) Axis: x = ____ x-int: (___, 0) & (___, 0) y-int: (0, ___) Vertex: (___, ___) Axis: ____________ x-int: ____________ Vertex: ________ y-int: _________ 5) 6) Axis: ____________ x-int: ____________ Vertex: ________ y-int: _________ Axis: ____________ x-int: ____________ Vertex: ________ y-int: _________
Algebra 2 Graphing Quadratics Practice 1 Name: _________________________ Date: __________________________ Directions: For each quadratic identify the axis of symmetry, vertex, x- and y-intercepts. Graph the parabola using the information. Show all work. 1) f(x) = x2 4 a = ___, b = ___, c = ___ 2) y = -2x2 + 4x Axis: x = ____ x-int: (___, 0) & (___, 0) y-int: (0, ___) Vertex: (___, ___) Axis: ____________ x-int: ____________ Vertex: ________ y-int: _________ 3) y = -x2 + 2x + 3 4) f(x) = x2 + 6x + 8 Axis: ____________ x-int: ____________ Vertex: ________ y-int: _________ Axis: ____________ x-int: ____________ Vertex: ________ y-int: _________